2. Понятие статистической гипотезы. Общая постановка задачи проверки гипотез.

Проверка статистических гипотез тесно связана с теорией оценивания параметров. В естествознании, технике экономике для вычисления того или иного случайного факта часто прибегают к высказыванию гипотез, которые можно проверить статистически (то есть, опираясь на результаты наблюдений в случайной выборке). Под статистическими подразумевают такие гипотезы, которые относятся или к виду, или к отдельным параметрам распределения случайной величины. Например, статистической является гипотеза о том, что распределение производительности труда рабочих, выполняющих одинаковую работу в одинаковых условиях, имеет нормальный закон распределения. Статистической будет также гипотеза о том, что средние размеры деталей, производимых на однотипных, параллельно работающих станках, не различаются.

Статистическая гипотеза называется простой, если она однозначно определяет распределение случайной величины , в противном случае гипотеза называется сложной. Например, простой гипотезой является предположение о том, что случайная величина распределена по нормальному закону с математическим ожиданием, равным нулю, и дисперсией равной единице. Если высказывается предположение, что случайная величина имеет нормальное распределение с дисперсией, равной единице, а математическое ожидание – число из отрезка , то это сложная гипотеза. Другим примером сложной гипотезы является предположение о том, что непрерывная случайная величина с вероятностью принимает значение из интервала , в этом случае распределение случайной величины может быть любым из класса непрерывных распределений.

Часто распределение величины известно, и по выборке наблюдений необходимо проверить предположения о значении параметров этого распределения. Такие гипотезы называются параметрическими.

Проверяемая гипотеза называется нулевой и обозначается . Наряду с гипотезой рассматривают одну из альтернативных (конкурирующих) гипотез . Например, если проверяется гипотеза о равенстве параметра некоторому заданному значению , то есть , то в качестве альтернативной гипотезы можно рассматривать одну из следующих гипотез: , где – заданное значение, причём . Выбор альтернативной гипотезы определяется конкретной формулировкой задачи.

Правило, по которому принимается решение принять или отклонить гипотезу , называется критерием и обозначается . Так как решение принимается на основе выборки наблюдений случайной величины , необходимо выбрать подходящую статистику, называемую в этом случае статистикой критерия . При проверке простой параметрической гипотезы в качестве статистики критерия выбирают ту же статистику, что и для оценки параметра .

Проверка статистической гипотезы основывается на принципе, в соответствии с которым маловероятные события считаются невозможными, а события, имеющие большую вероятность,– достоверными. Этот принцип можно реализовать следующим образом. Перед анализом выборки фиксируется некоторая малая вероятность , называемая уровнем значимости. Пусть – множество значений статистики , а – такое подмножество, что при условии истинности гипотезы вероятность попадания статистики критерия в равна , то есть .

Обозначим выборочное значение статистики , вычисленное по выборке наблюдений. Критерий формулируется так: отклонить гипотезу , если ; принять гипотезу , если . Критерий, основанный на использовании заранее заданного уровня значимости, называется критерием значимости. Множество всех значений статистики критерия, при которых принимается решение отклонить гипотезу , называется критической областью; область называется областью принятия гипотезы .

Уровень значимости определяет размер критической области . Положение критической области на множестве значений статистики зависит от формулировки альтернативной гипотезы . Например, если проверяется гипотеза , причём альтернативная гипотеза формулируется как: , то критическая область размещается на правом (левом) «хвосте» распределения статистики , то есть имеет вид неравенства , где – значения статистики , которые принимаются с вероятностями и при условии, что верна гипотеза . В этом случае критерий называется односторонним (соответственно – правосторонним и левосторонним). Если альтернативная гипотеза формулируется как , то критическая область размещается на обеих «хвостах» распределения статистики , то есть определяется совокупностью неравенств

В этом случае критерий называется двусторонним.

Расположение критической области для различных альтернативных гипотез показано рисунках, приведённых выше, где – плотность распределения статистики критерия при условии, что верна гипотеза , – область принятия гипотезы, .

Проверку параметрической статистической гипотезы с помощью критерия значимости можно разбить на этапы:

1. сформулировать проверяемую (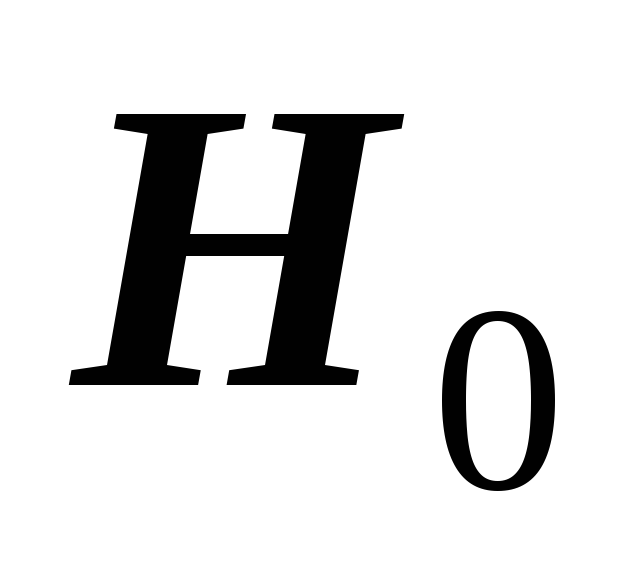) и альтернативную () гипотезы;

2. назначить уровень значимости ;

3. выбрать статистику критерия для проверки гипотезы ;

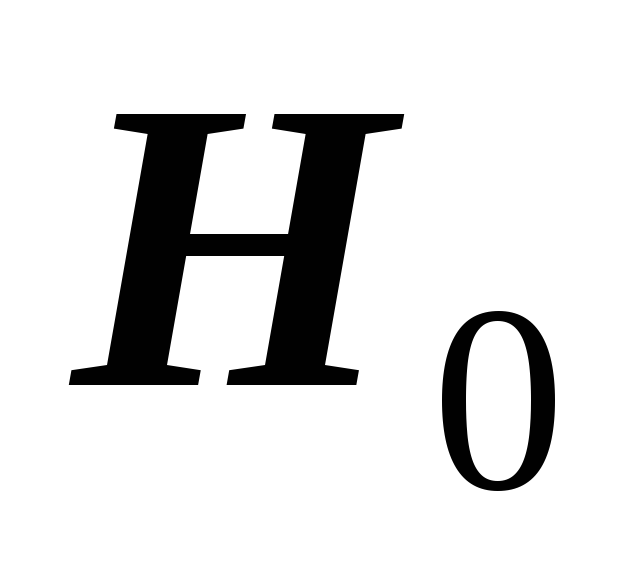4. определить выборочное распределение статистики при условии, что верна гипотеза ;

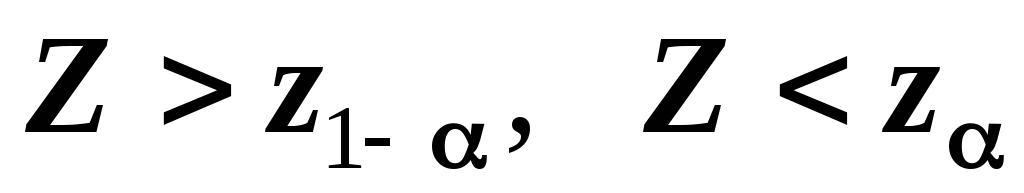5. в зависимости от формулировки альтернативной гипотезы определить критическую область одним из неравенств или совокупностью неравенств ;

6. получить выборку наблюдений и вычислить выборочные значения статистики критерия;

7. принять статистическое решение: если , то отклонить гипотезу 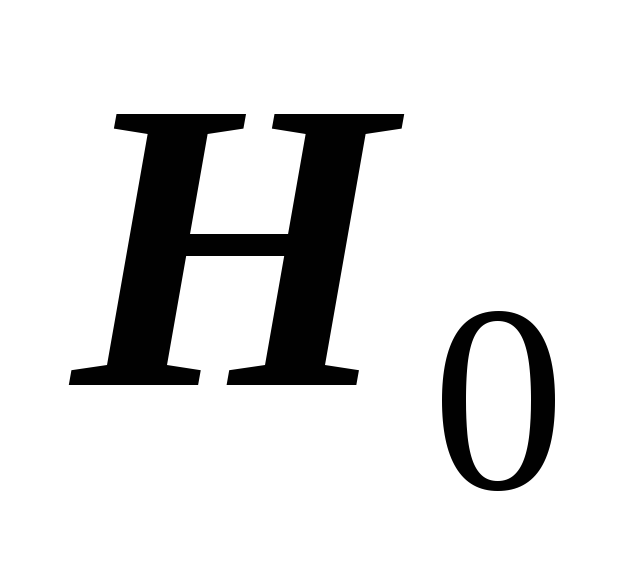как не согласующуюся с результатами наблюдений; если , то принять гипотезу , то есть считать, что гипотеза не противоречит результатам наблюдений.¹

ПРИМЕР 3. По паспортным данным автомобильного двигателя расход топлива на 100км пробега составляет 10л. В результате изменения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки проводятся испытания 25-и случайно отобранных автомобилей с модернизированным двигателем. Выборочное среднее расходов топлива на 100км пробега по результатам испытаний составило 9,3л. Предположим, что выборка расходов топлива получена из нормально распределённой генеральной совокупности со средним² и дисперсией . Используя критерий значимости, проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.

Решение. Проверим гипотезу о среднем нормально распределённой генеральной совокупности. Проверку проведём по этапам:

1. проверяемая гипотеза 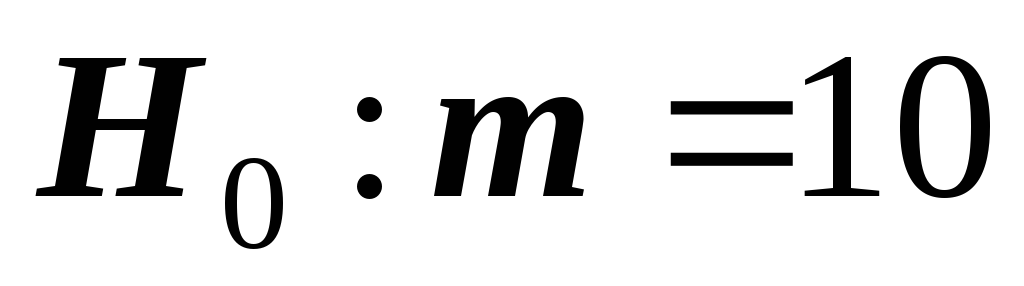; альтернативная гипотеза ;

2. уровень значимости ;

3. в качестве статистики критерия используем статистику математического ожидания – выборочное среднее ;

4. так как выборка получена из нормально распределённой генеральной совокупности, выборочное среднее также имеет нормальное распределение с дисперсией 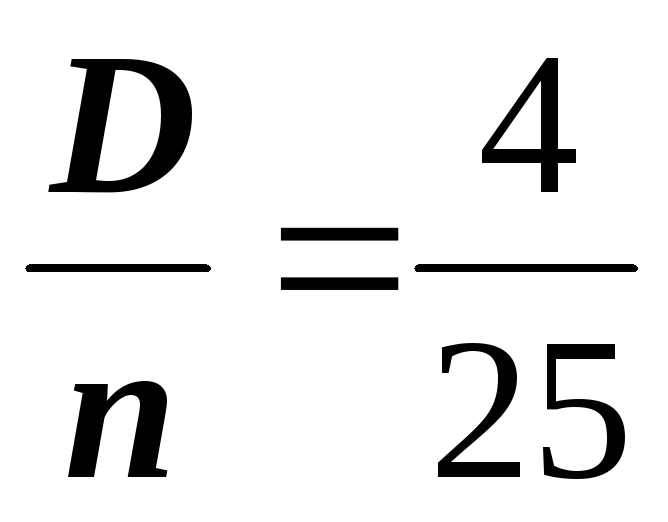. При условии, что верна гипотеза , математическое ожидание этого распределения равно 10. Нормированная статистика имеет нормальное распределение;

5. альтернативная гипотеза 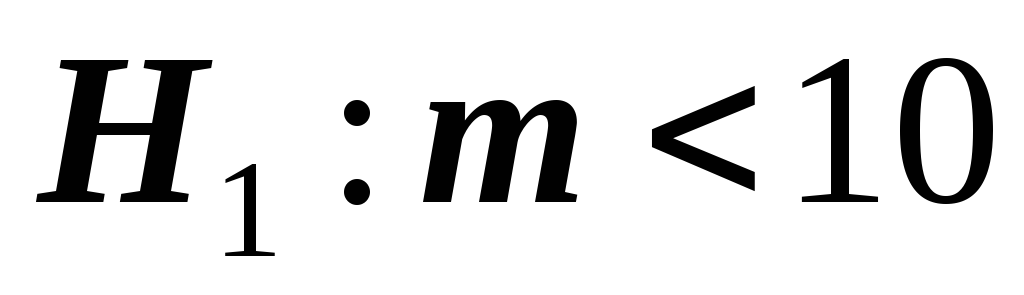предполагает уменьшение расхода топлива, следовательно, нужно использовать односторонний критерий. Критическая область определяется неравенством . По таблице (см. приложение) находим ;

6. выборочное значение нормированной статистики критерия

;

7. статистическое решение: так как выборочное значение статистики критерия принадлежит критической области, гипотеза 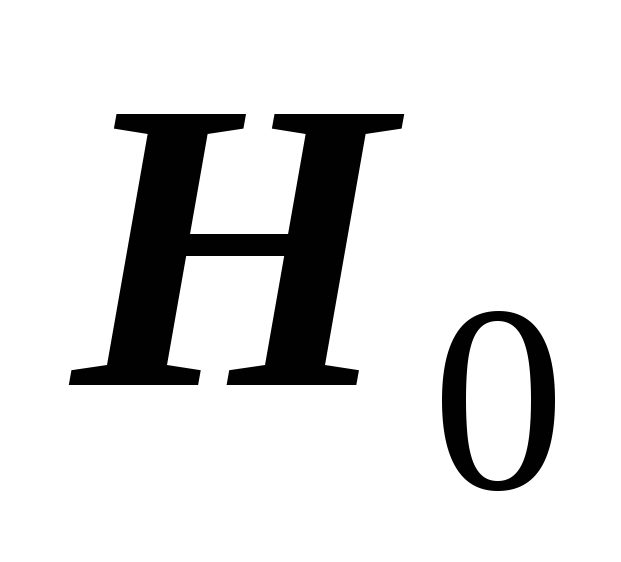отклоняется. Следует считать, что изменение конструкции двигателя привело к уменьшению расхода топлива. Границу критической области для исходной статистики критерия можно получить из соотношения 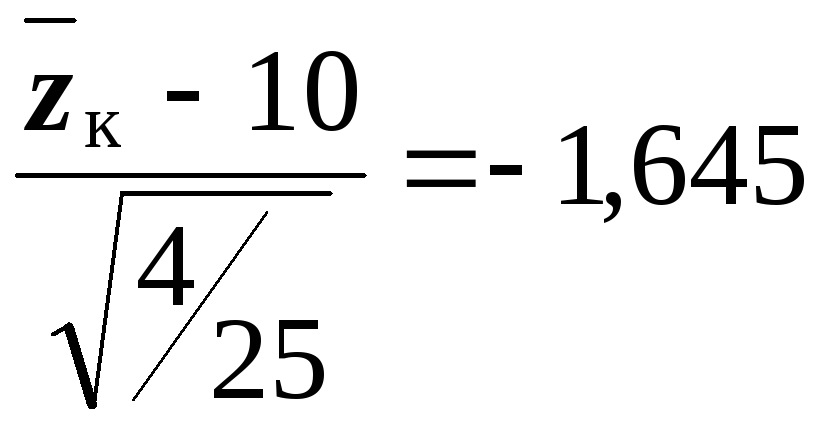, откуда 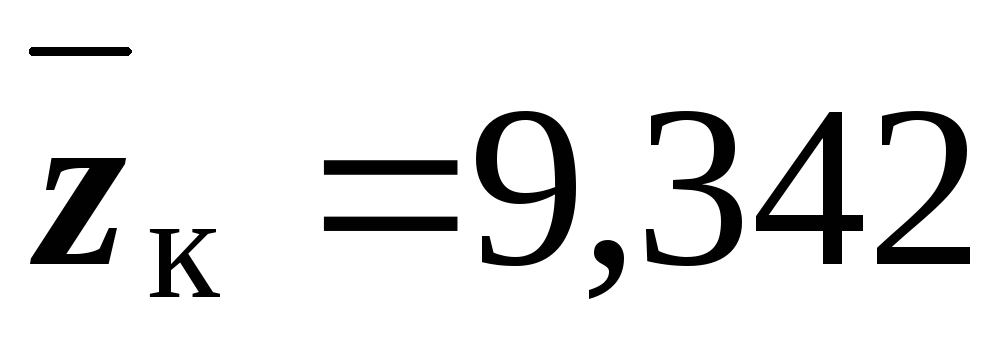. Таким образом, критическая область для статистики определяется неравенством .

Решение, принимаемое на основе критерия значимости, может быть ошибочным. Пусть выборочное значение статистики критерия попадает в критическую область, и гипотеза отклоняется в соответствии с критерием. Если, тем не менее, гипотеза верна, то принимаемое решение неверно. Ошибка, совершаемая при отклонении правильной гипотезы , называется ошибкой первого рода. Вероятность ошибки первого рода равна вероятности попадания статистики критерия в критическую область при условии, что верна гипотеза , то есть равна уровню значимости : .

Ошибка второго рода происходит тогда, когда гипотеза принимается, но в действительности верна гипотеза . Вероятность ошибки второго рода вычисляется по формуле:

.

ПРИМЕР 4. В условиях примера 3 предположим, что наряду с гипотезой рассматривается альтернативная гипотеза . В качестве статистики критерия снова возьмём выборочное среднее . Предположим, что критическая область задана неравенством . Найти вероятность ошибок первого и второго рода для критерия с такой критической областью.

Решение. Найдём вероятность ошибки первого рода. Статистика критерия при условии, что верна гипотеза , имеет нормальное распределение с математическим ожиданием, равным 10, и дисперсией, равной . используя таблицу (см. приложение), по формуле находим:

.

Это означает, что принятый критерий классифицирует примерно 8% автомобилей, имеющих расход 10л на 100км пробега, как автомобили, имеющие меньший расход топлива.

При условии, что верна гипотеза , статистика имеет нормальное распределение с математическим ожиданием, равным 9Б и дисперсией, равной . Нетрудно в этом случае найти вероятность ошибки второго рода, воспользовавшись формулой :

.

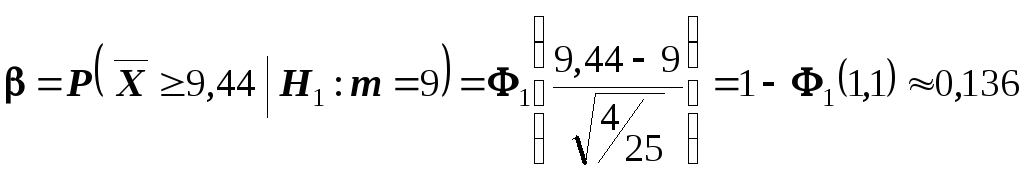Следовательно, в соответствии с принятым критерием 13,6% автомобилей, имеющих расход топлива 9л на 100км пробега, классифицируются как автомобили, имеющие расход топлива 10л.