2. Распределение Гаусса (нормальное распределение)

Наиболее известным и часто применяемым в теории вероятностей законом является нормальный закон распределения или закон Гаусса¹.

Главная особенность нормального закона распределения заключается в том, что он является предельным законом для других законов распределения.

Будем говорить, что непрерывная случайная величина Х, принимающая значения , подчиняется нормальному закону, если её плотность распределения (дифференциальная функция) имеет вид

.

Нетрудно видеть, что нормальное распределение определяется двумя параметрами: и . Достаточно задать эти параметры, чтобы задать нормальное распределение.

Заметим, что для нормального распределения интегральная функция имеет вид:

.

Покажем теперь, что вероятностный смысл параметров и таков: а есть математическое ожидание, – среднее квадратическое отклонение (то есть ) нормального распределения:

а) по определению математического ожидания непрерывной случайной величины имеем

Действительно

,

так как под знаком интеграла стоит нечётная функция, и пределы интегрирования симметричны относительно начала координат;

- интеграл Пуассона.

Итак, математическое ожидание нормального распределения равно параметру а.

б) по определению дисперсии непрерывной случайной величины и, учитывая, что , можем записать

.

Интегрируя по частям, положив , найдём

Следовательно .

Итак, среднее квадратическое отклонение нормального распределения равно параметру .

В случае если и нормальное распределение называют нормированным (или, стандартным нормальным) распределением. Тогда, очевидно, нормированная плотность (дифференциальная) и нормированная интегральная функция распределения запишутся соответственно в виде:

(Функция , как вам известно, называется функцией Лапласа (см. ЛЕКЦИЮ5) или интегралом вероятностей. Обе функции, то есть , табулированы и их значения записаны в соответствующих таблицах).

Свойства нормального распределения (свойства нормальной кривой):

1. Очевидно, функция на всей числовой прямой.

2. , то есть нормальная кривая расположена над осью Ох.

3. , то есть ось Ох служит горизонтальной асимптотой графика.

4. Нормальная кривая симметрично относительно прямой х = а (соответственно график функции симметричен относительно оси Оу). Следовательно, можем записать: .

5. .

6. Легко показать, что точки и являются точками перегиба нормальной кривой (доказать самостоятельно).

7. Очевидно, что

но, так как , то . Кроме того , следовательно, все нечётные моменты равны нулю. Для чётных же моментов можем записать:

8. .

9. .

10. , где .

11. При отрицательных значениях случайной величины: , где .

12. .

13. Вероятность попадания случайной величины на участок, симметричный относительно центра распределения, равна:

ПРИМЕР 3. Показать, что нормально распределённая случайная величина Х отклоняется от математического ожидания М(Х) не более чем на .

Решение. Для нормального распределения: . Далее, запишем:

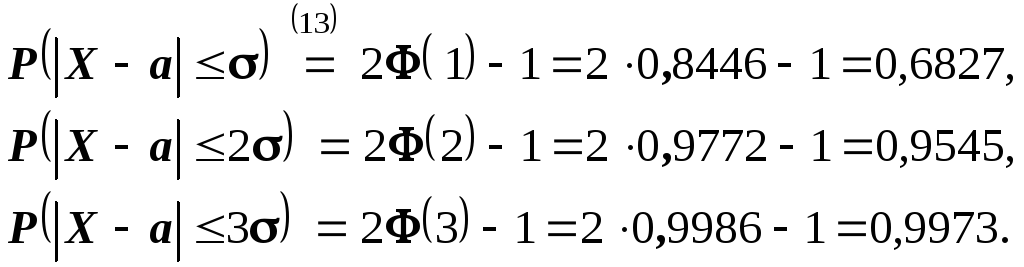
Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0, 0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий, можно считать практически невозможными¹.

Итак, событие с вероятностью 0,9973 можно считать практически достоверным, то есть случайная величина отклоняется от математического ожидания не более чем на .

ПРИМЕР 4. Зная характеристики нормального распределения случайной величины Х – предела прочности стали: кг/мм² и кг/мм², найти вероятность получения стали с пределом прочности от 31 кг/мм² до 35 кг/мм².

Решение.

.