
Теор.вер. (лекции) / Лекция 8
.docЛЕКЦИЯ 8
Основные законы распределения случайной величины
-
Равномерное распределение
-
Равномерное распределение дискретной случайной величины.
Пусть случайная
величина Х
принимает n
значений с вероятностями
![]() .
Данная случайная величина называется
равномерно распределённой случайной
величиной, если
.
Данная случайная величина называется
равномерно распределённой случайной
величиной, если
![]() для всех
для всех
![]() .
.
В этом случае:
- ряд распределения

-
функция распределения
![]()

- математическое
ожидание
![]() ;
;
- дисперсия
![]() .
.
ПРИМЕР 1. Случайная величина Х – выпадение числа очков на верхней грани игрального кубика при одном броске. Найти математическое ожидание случайной величины Х.
Решение.
Очевидно, что
![]() .
Так как
.
Так как
![]() ,
то, согласно определению, случайная
величина Х
распределена по равномерному закону.
Следовательно, в этом случае, можем
записать:
,
то, согласно определению, случайная
величина Х
распределена по равномерному закону.
Следовательно, в этом случае, можем
записать:
![]() .
.
-
Равномерное распределение непрерывной случайной величины.
Непрерывная случайная величина подчиняется равномерному закону распределения, если её возможные значения лежат в некотором определённом интервале, в пределах которого все значения равновероятны, то есть обладают одной и той же плотностью вероятности. Другими словами, распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, дифференциальная функция имеет постоянное значение.
Случайные величины, имеющие равномерное распределение вероятностей, часто встречаются на практике. Например, при снятии показаний измерительных приборов. Ошибка при округлении отсчёта до ближайшего целого деления шкалы является случайной величиной, которая может с постоянной плотностью вероятности принимать любые значения между двумя соседними делениями. Таким образом, данная случайная величина имеет равномерное распределение.
Найдём дифференциальную
функцию (плотность) равномерного
распределения, считая, что все возможные
значения случайной величины Х
заключены в промежутке
![]() ,
на котором дифференциальная функция
сохраняет постоянное значение, то
есть
,
на котором дифференциальная функция
сохраняет постоянное значение, то
есть
![]() .
.
По условию Х
не принимает значений вне промежутка
![]() ,
поэтому
,
поэтому
![]() при всех
при всех
![]() и
и
![]() .
.
Найдём значение
постоянной С.
Так как все возможные значения случайной
величины принадлежат промежутку
![]() ,
то справедливо:
,
то справедливо:
![]() .
.
Итак, закон
равномерного распределения случайной
величины на отрезке
![]() (здесь
(здесь
![]() )
аналитически можно записать так:
)
аналитически можно записать так:

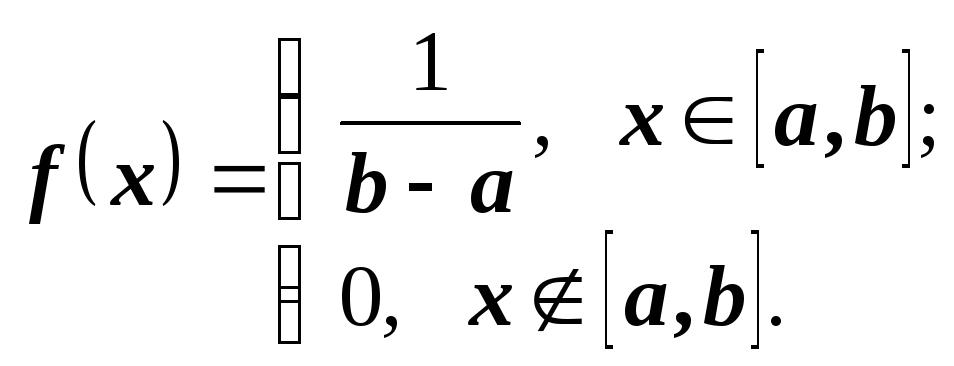
Найдём теперь интегральную функцию равномерного распределения непрерывной случайной величины. Для этого воспользуемся формулой
![]() .
.
Тогда:
-
если
 ,
то
,
то
 и, следовательно,
и, следовательно,
 ;
; -
если
 ,
то
,
то
 и, следовательно
и, следовательно
![]() .
.
-
если
 ,
то
,
то
 .
.
Итак, искомая интегральная функция распределения аналитически может быть записана так:


Свойства равномерного непрерывного распределения:
-
 ;
;
-
 ;
; -
моды распределение не имеет;

5.
![]() ;
;
-
В силу симметрии распределения все нечётные моменты равны нулю.
![]() .
.
Тогда
![]() .
.
-
 .
.
ПРИМЕР 2. Троллейбусы идут строго по расписанию и с интервалом в 6 мин. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать троллейбус менее двух минут.
Решение. Время ожидания троллейбуса есть непрерывная случайная величина Х, имеющая равномерное распределение на промежутке [0,6], так как с равной вероятностью время ожидания может быть любым в этом промежутке. Тогда

Тогда
![]() .
.
-
Гипергеометрическое распределение
Гипергеометрическое распределение играет важную роль в области статистического контроля качества.
Будем говорить, что дискретная случайная величина Х, принимающая целочисленные значения X={0,1,2,…,n}, распределена по гипергеометрическому закону, если вероятности этих значений определяются выражением
 ,
,
где N – объём партии изделий;
n – объём выборки из данной партии изделий;
D – число дефектных изделий в данной партии изделий;
d – число дефектных изделий в соответствующей выборке изделий.
Свойства гипергеометрического распределения:
-
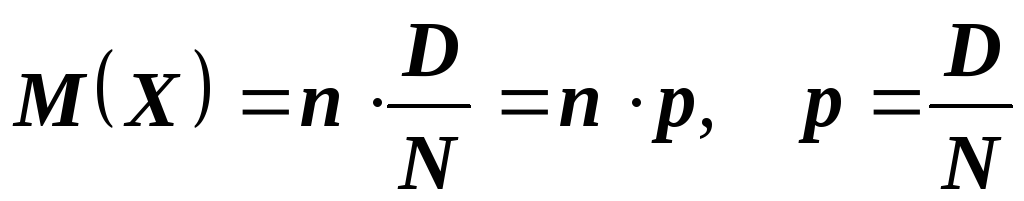 (доказать
самостоятельно);
(доказать
самостоятельно);
-
 (доказать
самостоятельно);
(доказать
самостоятельно);
-
при
 гипергеометрическое распределение
приближается к биномиальному распределению
(о котором поговорим немного позднее).
гипергеометрическое распределение
приближается к биномиальному распределению
(о котором поговорим немного позднее).
ПРИМЕР 3.
Партия из
100 изделий содержит 10% брака. Для контроля
выбрано 5 изделий. Необходимо определить
вероятность того, что в выборке меньше
двух бракованных изделий. Найти
![]() для случайной величины Х
– числа дефектных изделий в данной
выборке изделий.
для случайной величины Х
– числа дефектных изделий в данной
выборке изделий.
Решение. Данная дискретная случайная величина Х={0,1,2,3,4,5}очевидно подчиняется гипергеометрическому закону распределения вероятностей. В нашем случае N = 100, D = 10, n = 5. Вероятность того, что в выборке ровно d бракованных изделий равна
 .
.
Вычислим (приближённо)
значения
![]() и запишем их в таблицу
и запишем их в таблицу
|
Х |
0 |
1 |
2 |
3 |
4 |
5 |
|
|
р |
0,583 |
0,340 |
0,070 |
0,007 |
0,000 |
0,000 |
|
Найдём функцию распределения:

Аналогично найдём
![]() .
.
Заметим, что
![]() .
То есть вероятность
того, что в выборке меньше
двух бракованных изделий равна 0,923.
.
То есть вероятность
того, что в выборке меньше
двух бракованных изделий равна 0,923.
Далее, найдём
![]() .
.
Замечание: Сравним полученные значения математического ожидания и дисперсии с соответствующими значениями (см. свойства гипергеометрического распределения):
![]() ,
,
![]()
Как видим, не доказывая формулы для M(X) и D(X), на примере мы убедились в их справедливости.
-
Биномиальное распределение
Биномиальное распределение вероятностей является самым распространённым распределением для дискретных случайных величин.
Итак, пусть
производится n
независимых испытаний, в каждом из
которых событие А
может
появиться, либо не появиться. И пусть,
вероятность наступления события во
всех испытаниях постоянна и равна р
(следовательно, вероятность непоявления
![]() ).
Рассмотрим в качестве дискретной
случайной величины Х
– число появлений события А
в этих испытаниях.
).
Рассмотрим в качестве дискретной
случайной величины Х
– число появлений события А
в этих испытаниях.
Поставим перед собой задачу: найти закон распределения величины Х. Для её решения требуется определить возможные значения случайной величины Х и их вероятности.
Очевидно, событие
А
в n
испытаниях может либо не появиться,
либо появиться 1 раз, либо 2 раза, . . . ,
либо n
раз. Таким образом, нетрудно записать
возможные значения случайной величины
![]() .
Остаётся найти вероятности этих возможных
значений, для чего достаточно
воспользоваться формулой Бернулли (см.
Лекцию 5):
.
Остаётся найти вероятности этих возможных
значений, для чего достаточно
воспользоваться формулой Бернулли (см.
Лекцию 5):
![]() ,
где k
=
0,1,2,…,n.
,
где k
=
0,1,2,…,n.
Формула Бернулли и является аналитическим выражением искомого закона распределения.
Биномиальным называют распределение вероятностей дискретной случайной величины, определяемое формулой Бернулли.
Запишем биномиальный закон в виде таблицы:
|
Х |
0 |
1 |
2 |
. . . |
k |
. . . |
n – 1 |
n |
|
р |
|
|
|
. . . |
|
. . . |
|
|
Свойства биномиального распределения:
-
 .
.
Действительно:

-
 (заметим, что
(заметим, что
 при
при
 )
(доказать самостоятельно)
)
(доказать самостоятельно)
-
 .
.
-
 .
.
ПРИМЕР 4. Имеется три станка, коэффициент использования по времени которых составляет 0,8. Определить вероятность того, что в середине рабочей смены при нормальных условиях производства из данных трёх станков будет работать не более двух.
Решение.
Работа каждого станка – события
независимые. Вероятность того, что
станок будет работать равна р=0,8
(следовательно q=1-0,8=0,2).
Пусть случайная величина Х
- число одновременно работающих станков,
то есть
![]() .
Очевидно, что вероятности значений
случайной величины Х
подчиняются биномиальному закону
распределения с параметрами р=0,8;
q=0,2;
n=3.
Значит
.
Очевидно, что вероятности значений
случайной величины Х
подчиняются биномиальному закону
распределения с параметрами р=0,8;
q=0,2;
n=3.
Значит
![]() ,
k
= 0,1,2,3.
,
k
= 0,1,2,3.
Требуется определить
вероятность
![]() .
По определению
.
По определению
![]() .
.
Так как:

Тогда
![]() .
.
