
Martynyuk_A_N_Diskretnaya_matematika
.pdf9. (x1 x2)= x1 x2; |
(x1 x2)= x1 x2; |
* F
6 9 86 (11-14)
(15, 16), A 9 5 C 5 .
10.xi5f(x1, x2,..., xi, xi,..., xn)=xi5f(x1, x2,..., 1, 0,..., xn);
11.xi5f(x1, x2,..., xi, xi,..., xn)= xi5f(x1, x2,..., 0, 1,..., xn);
12.xi f(x1, x2,..., xi, xi,..., xn)=xi f(x1, x2,..., 0, 1,..., xn);
13.xi f(x1, x2,..., xi, xi,..., xn)= xi f(x1, x2,..., 1, 0,..., xn)
14.f(x1, x2,…, xi,…, xn)=(xi5f(x1, x2,…,1,…, xn)) ( xi f(x1, x2,…, 0,…, xn));
15. f(x1, x2,…, xi,…, xn)=(xi f(x1, x2,…, 0,…, xn))5( xi f(x1, x2,…, 1,…, xn))
2 9 9 8 5
9 – 5 6 6
6 8 6 4.
= C 6 6 6
C 9 8 4 8.
4 &. ) & ' (% ):
( (=(( ()51=(( ()(( ()=( ((5()=( 0=(;
%) :
( (5 =((51) ((5 )=(5(1 y)=x 1=() 1 "-4 ':
( (5 =(( ()5(( )=15(( y)=( y
24.2.% S , . % / $ +
<8 8 6 6 6 9 8, A 9 :
9 5 = y15-i , 0 , , 15. - 5 4 9 C
:
0= 1 1= 0;
3z : :
(= ( ();
3z 6 6:
(15(2= ((1/(2);
(1T(2= ( (1+(2);
(1[(2= ((1N(2);
(1 (2= ((1R(2);
(1T(2= ((1+(2);
(1>(2= (1+ (2);
(1+(2= ((1T(2);
(1N(2= ((1[(2);
(1R(2= ((1 (2);
(1+(2= ( (1T(2).
< 6 9 :, A 8 5- 6 6, + +
, 9 : 5 4 5 C , A
5 8 5- 6 { 0, 15}, {y1, y14}, {y2, y13}, {y4, y11},
{y6, |
y9}, |
{y7, y8} A : C +. |
|
… 4 , A |
|
((1>(2)=(1 (2;((1N(2)=((1 (2)( (1 (2) .
121

> 5 9 5 6 : “ 0”, < 6<,
'+ <x1 x2< ’+ <61562<. B 9 9 5 8 –
-* 4 + (4 ). ? , + 5 9:
(1 (2= ( (15(2);
(15(1=0;((1 (1)=0;
(15(2= ( (1 (2).
< :, A 8 + 5 ’+ +
'+ +.
D A 8 ' 5 ( '+
'+), 9 5.
4 &. ((1 (2) ((3 (4)=(1 (2 (3 (4
2 9, 6 8 5 4 5 ( ), 9 9
, A , '+ '+ 5C : 5
6 , '+, '+.
4 &. (( )5z=x y5z=( x y) z= x y z.
24.3. * E H / $ + G + +F G
( 8 4 8 : & ". 1 : :
'+ '+. < + 9 + ,
9 : . |
|
|
4 &. |
- |
((1 (2)5((3 (4) |
4 & " P |
((15(2) ((3 (4). |
& " P f ( & ' $ ' |
>. |
.% |
|
( ' P f % ( & P f ,
% 0>1, 1>0.
4 &. |
(1 |
(2 |
f=x1 x2 |
1 |
x1 |
x2 |
f =x15x2 |
0 |
0 |
0 |
|
1 |
1 |
|
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
1 |
1 |
|
0 |
0 |
0 |
|
) ` ' |
' |
% $ |
& ' |
|
( . |
|
|
||
X1 |
x2 |
f =x15x2 |
|
|
0 |
0 |
0 |
|
|
0 |
1 |
0 |
|
|
1 |
0 |
0 |
|
|
1 |
1 |
1 |
|
|
z , 5 , : 5 |
||||
& "$. |
|
|
|
|
4 &. |
1=(15(2 (15(3 (25(3 y2=((1 (2)5((1 (3)5((2 (3) – & " ' |
|||
P, % y= 1= 2 – & " P. |
|
|
||
. : 1 . / f1 f2 /, * 0 . / f1 f2 |
||||
/, . |
|
|
||
f1=f2;f1 =f2 |
|
|
|
|
4 &. |
( (( )=( |
; |
( (( )=( |
|
( ( ( )=( ; ( ( ( )=( .
. () *): : 1 + / * . / f '3 ) 0
’3 ) 0, «0» «1», «1» «0», . / f , * 0.
122
. 8 6 5 9
9 8 4 8, 6 .
24.4. B + +F G $;
. 8 4 8 5 8 5C 4 5 6, 9 5 8 4 8
9 . M 4 8 4 + (2, 2, 1), : 5
8 , : 5 8 + 4 8 +, A 5 + 5
9 1 - 10.
-6 9 *.
>. 9 % 9=(>(A), { , , } ' % $ %$ &
$ A, % % - (2, 2, 1).
>. 9 % 9 9- $' P, 8 ' 8
& & & ' ( (%
).
-6 : 5 9 9 + 1(*), *={m1,
m2,..., |
mn} |
|
9 + |
6 |
|
1n |
n: G: >(A);>n |
|
|
|
|
||
. 9 *- * : b=(b1,b2,.., bn), bi=1, A mi M-, |
||||||
bi = 0, A mi - 4 mi M. |
1n |
8 4 8 |
4: |
|||
-6 |
|
9 |
6 |
|||
M-=(1n,{ , , }, 5 8 5-6 C=<C1, C2,..., Cn> H=<H1, H2,..., Hn> + 5 8:
1.C H=<C1 H1, C2 H2,..., Cn Hn>
2.C H=<C1 H1, C2 H2,..., Cn Hn>
3.C=< C1, C2,..., Cn>.
C H + 5 4
. |
|
|
4 &. |
C=10110; |
H=00101; |
|
C H=10111; |
C=01001; |
|
C H=00100; |
H=11010. |
. 6 5 8 5- T *, A A :
+ 4 8 T *.
B 4 8 8 4 8 9, : -
9 8':, , 9
4 , T *: G:
9'-, G-1: 9-'. |
|
|
|
|
|
|
4 &. A={m1, m2, m3, m4}; M1={m1, m2, m3}; M2={m2, m3, m4}; |
|
|
||||
|
M1={m4}; |
|
M2={m1}; |
1 2={m2, |
m3}; |
1 2= |
={m1, m2; m3, m4};
'-:
1'b1=<1, 1, 1, 0>; 2'b2=<0, 1, 1, 1>;
M1' b1=<0, 0, 0, 1>; M2' b2=<1, 0, 0, 0>;1 2'b1 b2=<0, 1, 1, 0>; 1 2'b1 b2=<1, 1, 1, 1>.
123
+H . % ,
1. Y ' % $ %$, $ $ $ % %?
2.S & ' ( " $'?
3.S ` ' & & $'?
4.S & ' % ( P & % ' ?
5.S & ' % ( P & (
'?
6.S & & P " & & ( (
8 % ( P ?
7.S % P & ", & "
& " % P?
8.3 & "?
9.o , 8 % % $, 8 %( & & %
%?
10.Y % $ %$ & " ( ?
11.S % P?
% +
+
24.1.E -.9. 0 & . – N4%.: 4, 2001. - N.81-88.
24.2.S% " N.>. > & &$ . – A.: E, 1979. - N.10-
19.
24.3.N " >.4. A " . – _.: .(, 1975. -
N.504-522.
0 &
24.4.d % >.9. + b & " . – A.: >b `.`., 1986. - N.47-
50.
24.5.1 P d., 1 .. N & %. – A.: A, 1976. -
N.139-150.
0 ( '
24.6.A & & & ' ( % & «+ & » & & P P ( 6.0804, 6.0915 / +.A. A$ . – +&: +E43, 2001. – N.27-30.
24.7.d d.4., N 9.9. N% & & " . –
A.: E, 1973. - N.30-38.
124
? 25. A B# @ A. D. A !
" %
% š , P '
. " " % {[, }, ’' % (
P ", P ' ' , " 4. ) &
& ( (. 3 ’' & & : 25.1. 9 % š
25.2. . % ( P "
25.3.- '
25.4.( ') (
25.5._ & ( (
25.1. +F G @ F +
M 4 8 ™ 4 9 8 6 6 :
[ '+ .
>. 9 % š – 9=(>, {[, }, 1), & >
– ( % ( P ", % – {[, }, & & %
$ &.
? 4 8 ™ 4 - (2, 2), 8 : 8 4 8 +. 1 4 8 ™ 4 + 5 9:
1. ([ = [(; |
( = ( |
$H. |
|
2. ([( [z)=(x[y)[z; |
x (y z)=(x y) z |
C H. |
|
3. x (y[z)=(x y)[(x z)
* G H '' C.
4. x[0=x; |
x 0=0; |
x[1= x; |
x 1=x |
+ F CH. |
|
5. ([(=0; |
( (=( |
% * , *$% H. |
|
6. x[x=1; |
x x=0 |
* % ,. |
|
7. x[(x y)=x y; |
x (x[y)=x[(x y) |
% F+ ,. |
|
8. x[( y z)=([ ; |
x ( x[y)=( |
B+ E-CH F. |
|
9. (x[y) (x[y)=0; |
(x y)[(x y)=x |
+ ' ,. |
|
10. (x[y)= x[y=x[y; |
(x y)=(x y)[1 |
* F. |
|
11. x[y=(x y) ( x y); |
x[y=(x y) ( x y) |
% + * G + G ..
12.x[y= x[y.
13.x y=x[y[(x y)
% + * G . @ F +;
14.x[y=0;x=y.
15.x[y=z'x[z=y G z[y=x.
125
? 9 4, 6, 13 + 5 8 5- 8 4 8
4 8 ™ 4, 4 + 9 4, 6, 11 9
6 4 8 ™ 4 8 4 8.
4 &. x ( x y) = x ((1[x) y) = x ((1[x)[y[(1[x) y))= x (1[ [x[y[y[(x y)) = x[(x x)[(x y x) = x[x[(x y) = xy;
1[x[y= x[y=(xy) ( x y).
> 4 8 ™ 4 {[, } + «1» +:
8 5 .
25.2.% G + ( / C E
>. 3 % % % ( P " & <n< ( f(x1, x2,..., xn)
22^n & $' '' % ( P " ( ’' & ' (
P "):
1. - , 8 %$' «0», % P, 8 ' ( % (
"$' ' : f(x1, x2,..., xn)'f(0, 0,..., 0)=0.
4 &. |
f(x1, x2)=x1 x2'f(0, 0)=0. |
2. - , 8 %$' «1», % P, 8 & ( % ( |
|
"$' & : |
|
f(x1, x2,..., xn)'f(1, 1,..., 1)=1. |
|
4 &. |
f(x1, x2)=x1 x2' f(1, 1)=1. |
3.N & " P, 8 "$' % &'-( & (
( % (:
4 &. f(x)= x'f(0)=1, f(1)=0.
4." P, 8 $' % š % , 8
& % (:
f(x1, x2,..., xn)=a0[ a15x1[a25x2[...[an5xn,
& 0, 1, 2,..., n – , 8 "$' 0 1
4 &. f(x)=1[ x1[ x2.
5. A P, 8 & % &'-( & ( & ( % <x11,
x12,..., x1n> <x21, x22,..., x2n>, & <x11, x12,..., x1n> , ,<x21, x22,.., x2n>, "$'
& , % f(x11, x12,..., x1n), f(x21, x22,..., x2n).
4 &. |
f1(x1, x2)=x1 x2, f2(x1, x2)=x1 x2, f3(x1, x2)=x2 |
||
<x1, x2> |
f1: |
f2: |
f3: |
<0, 0> |
0 |
0 |
0 |
<0, 1> |
1 |
0 |
1 |
<1, 0> |
1 |
0 |
0 |
<1, 1> |
1 |
1 |
1 |
6 ’ , ++ 5 6 .
>. 1 P xi, xj, 8 f(…, xi,…,xj,…) = f(…, xj,…,xi,…). 1 P , 8
(.
4 &. - f = x1 x2 x3 x1 x2x3 ( x1 x3. - f = x1x2x1x3 x2x3 .
126
25.3. D C +H %
>. N % ( P " ' P ' $, 8
( P " & & % &'- P$ % ( P ". 4 &. N P " { , , } P ' $, P "
{[, } P ' .
D A 5 : «0» «1»,
% P ' . z 5 +: %
.
4 &. N P " {[, }, 8 $ &, % {{[, } 1}, % P ' .
>. N % ( P " ' ' %, 8 & % &'- P $ $ .
4 &. A ' " % { , }, { , , } '
%.
>. 3 ' P " % , 8 & , % , 8 % &'- P " & P$, 8
' , ' P ' . z 5 , 9 5 4 6
9 6 8 6 , + 5 P ' .
1 5 : 5 &, A 5
5 , A : 4 6
9 6 8 6 .
4 &. N P ", 8 %$' &$, P '
, P ", 8 %$', P ' . 4 ` & $.
.) / (* (): M/ ?, 1 +
+ / . ) * + / 3, + , 1 + /3 / +
. ) 3, 1 + ? 2 «0», + . ) 3, 1 + ? 2
«1», + . ) 3, 1 *, + . ) 3, 1 / *, +
. ) 3, 1 .
? 9 5 5
86 6 , A : .
4 &. > ( % ( P ".
. % 25.1.
/ . ) |
G- |
; +. |
; +. |
;- |
; /-* |
;- |
|
/ |
”0” |
”1” |
0 |
|
|
5 “0” |
0 |
|
+ |
+ |
|
|
5 “1” |
1 |
+ |
|
+ |
|
|
\ |
x |
+ |
+ |
|
|
+ |
5'3 ) |
x1 x2 |
|
|
+ |
+ |
|
M'3 ) |
x1 x2 |
|
|
+ |
+ |
|
E |
x1[x2 |
|
+ |
+ |
|
+ |
/ “2” |
x1/x2 |
+ |
+ |
+ |
+ |
+ |
n |
||||||
n .. |
|
+ |
+ |
+ |
+ |
+ |
E / ( |
x1Rx2 |
) % &, 8 P " { '$ , }, {&'$ ,
}, {` ( • PP}, { 4} & '$' 4. N P " { , , } $ " % " %.
127
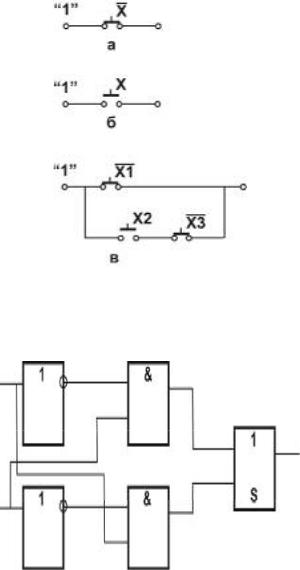
25.4. F- (%$+H) ($
2 8 6 8 + 5 + 5 4
, A : , A 8 + 6 4 :+. ˜6 6 + 5 8 , 6 - . 2
4 6 + 5 , , 8 C 4. ( 4 9 8 , A :. .8
8 6 4 6 8 + 5 ': 4 6 .
4 &. " ( ) ().
. 25.1. " ' ( & ' ( P "- y1 = x; % - y2 = x; - 3 = x1 (x25x3)
4 &. ( ’ .
. 25.2. ( & P y = (x15x2) ( x15 x2)
128
25.5. - . *- . + F-( ($
., A + 5 8 , + 5
. $ ($ : 5 ': ( ) 4 6 . < 8 4 6, A : 8 , : 5
&$ .
< 8 4 6 : 5 &$
.
* 9 +, A : 8 , 4 + 6 +, A :
, : : 5. 8 9 8
4 + 5 6 , 9, 9 8 5 6, A
+ 5 8 +. ? 4 6 + 5 .
, A 8 5C : 8 5C 4 6. .
9 8 5C + , A 5 C 6 4 6 . ? , 9 8 5C 4 6 86 A
4 4 + 4 6 5.
>. _ & ( ( % % ( , , )
& ' & :
1.> ( & % P & ' N0E- (N_E-).
2.) &$ " &, % P & ' &
& 0E- (_E-), 8 ' ' ' (%) ( ",
&& ' $, % 0E- ( _E-) .0E- (._E-).
3.0 .0E- (._E-) % & ' (.
+ &:
(x15x2) (x15x2)=x1; (x1 x2) (x1 x2)=x1.
+ :
x1 (x15x2)=x1; x1(x1 x2)=x1.
( 5 4 6 5 ,
6 5C 4 9, 8
P - .0E- ._E-. > 6 6 5 ' (A0E- A_E-),
5 6 9 8 5. l – 9
9 6 (N E-).
4 &. y=x1x2 x3 x1x2x3 x1x2x3 N0E- y=x1x2 x3 x1x2x3 x1x2x3 x1x2x3
y=x1x2 x2x3 |
A0E- |
y=x2(x1 x) |
N E-P ( A_E-). |
|
+H . % , |
1.Y ' %$ š , 8 $ $
$ % š ?
2.S ( " % š $'?
3.S P P % % % š
?
4.S % ( P " $'?
5.S ' P & ’ ?
6.S % ( P " P ' $, %
P ' $?
7.Y % , ' %?
8.S P " P ' $?
9.S $' P ' ,
& ?
10.Y ` " 4?
129
11.Y $ ($?
12.S &$' & ? Y $ &$
( (?
% +
+
1.E >.d., N 9.>. 4 & & -
(. 0 & ( (. – _.: 3 %-
& " % b ` %, 1992. - N.137-148.
2.E -.9. 0 & . – N4%.: 4, 2001. - N.94-98.
3.d % >.9. + b & " . – A.: >b `.`., 1986. - N.55-
73.
0 &
4.S% " N.>. > & &$ . – A.: E, 1979. - N.23-
35.
5.N " >.4. A " . – _.: .(, 1975. -
N.504-522.
0 ( '
6.A & & & ' ( % & «+ & » & & P P ( 6.0804, 6.0915 / +.A. A$ . – +&: +E43, 2001. – N.30-35.
7.d d.4., N 9.9. N% & & " . –
A.: E, 1973. - N.50-77.
130
