- •Розрахунково-пояснювальна
- •Завдання 1
- •1.2 Розв’язок системи нелінійних рівнянь вузлових напруг у формі балансу струмів з використанням метода Гауса на кожному кроці ітераційного процесу.
- •1.3 Розв’язок системи нелінійних рівнянь вузлових напруг у формі балансу струмів методом Гауса – Зейделя.
- •1.4 Формування системи нелінійних рівнянь вузлових напруг у формі балансу потужностей.
- •1.5 Розрахунок струмів і потужностей гілок.
- •Завдання 2
- •Завдання 3
- •Висновок:
- •Список літератури:
1.4 Формування системи нелінійних рівнянь вузлових напруг у формі балансу потужностей.
Перед формуванням системи рівнянь вузлових напруг у формі балансу потужностей необхідно перетворити схему заміщення у еквівалентну схему заміщення з 2 незалежними вузлами.
Розносимо навантаження вузла 2 у вузли 1 і 3:


Перевіряємо:

Розраховуємо значення потужності у вузлі 1 і 3:


З’єднуємо послідовно гілки 2 та 5:

Знаходимо провідність еквівалентної гілки:
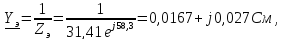
Результуюча провідність між вузлами 2 і 4:

Перейменовуємо вузол 3 у вузол 2, вузол 4 у вузол 3, гілку 4 у гілку 3, еквівалентну гілку 1-3 у гілку 2.

Система нелінійних алгебраїчних рівнянь вузлових напруг у формі балансу потужностей, записана у виразах для небалансів потужностей у вузлах, має вигляд:



 Якщо
в якості невідомих при рішенні рівнянь
використовуються модулі і фази напруг
у вузлах
Якщо
в якості невідомих при рішенні рівнянь
використовуються модулі і фази напруг
у вузлах
 ,
, ,
то після підстановки активних і реактивних
складових провідностей вузлів, активних
і реактивних потужностей у вузлах,
напруги базисного вузла і прирівнюючи
окремо дійсні і уявні частини комплексів,
отримуємо систему трансцендентних
рівнянь вузлових напруг у формі балансу
потужностей при невідомих
,
то після підстановки активних і реактивних
складових провідностей вузлів, активних
і реактивних потужностей у вузлах,
напруги базисного вузла і прирівнюючи
окремо дійсні і уявні частини комплексів,
отримуємо систему трансцендентних
рівнянь вузлових напруг у формі балансу
потужностей при невідомих ,
, .
Для к-го вузла, рівняння вузлових напруг,
записане у вигляді функцій небалансів
активних і реактивних потужностей у
вузлі, має вигляд.
.
Для к-го вузла, рівняння вузлових напруг,
записане у вигляді функцій небалансів
активних і реактивних потужностей у
вузлі, має вигляд.

Рисунок 1.3 – Перетворена схема заміщення.


Де:



 Для
схеми заміщення на рисунку 2 розрахуємо
власні та взаємні провідності вузлів:
Для
схеми заміщення на рисунку 2 розрахуємо
власні та взаємні провідності вузлів:






Складаємо матрицю вузлових провідностей:

Розносимо її на 2 частини: дійсну та мниму:


Задаємося початковим наближенням невідомих:

Розраховуємо потужності у вузлах. Так як потужність розподіляється між вузлом 2 та базисним вузлом, то:
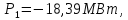



Розраховуємо небаланси активних та реактивних потужностей на нульовому кроці ітерацій:








 Для
формування лінеаризованої системи
рівнянь необхідно одержати вирази для
перших похідних функцій небалансів
активних і реактивних потужностей у
вузлах по модулях і фазах невідомих
напруг. Ці вирази одержуються у такому
вигляді:
Для
формування лінеаризованої системи
рівнянь необхідно одержати вирази для
перших похідних функцій небалансів
активних і реактивних потужностей у
вузлах по модулях і фазах невідомих
напруг. Ці вирази одержуються у такому
вигляді:








По знайденим небалансам активної та реактивної потужності складаємо матрицю Якобі на нульовому кроці ітерації. За допомогою програми Mathcad рішаємо матрицю.



 Уточнюємо
значення напруг і фазних кутів:
Уточнюємо
значення напруг і фазних кутів:




Знаходимо значення напруг і фазових кутів на першому кроці, розраховуємо небаланси активної та реактивної потужності на другому кроці ітерації:


 Продовжуємо
ітераційний процес, доки небаланси не
стануть меншими заданої точності
Продовжуємо
ітераційний процес, доки небаланси не
стануть меншими заданої точності
 .
Розрахунок
проводимо на ПК, результати записуємо
до таблиці:
.
Розрахунок
проводимо на ПК, результати записуємо
до таблиці:
Таблиця 1.7 – Результати розрахунку на ПК
|
|
0 |
1 |
2 |
3 |
|
|
115 |
111,0084 |
110,8574 |
110,8568 |
|
|
0 |
-0,0077933 |
-0,008009 |
0,008012 |
|
|
115 |
111,3031 |
111,1655 |
111,1652 |
|
|
0 |
-0,01174 |
-0,012206 |
0,012209 |
|
|
-18,39 |
-0,80486 |
-0,000216 |
-0,0015 |
|
|
-17,82 |
-0,48095 |
-0,000467 |
-0,00035 |
|
|
-23,8 |
-0,77369 |
-0,15098 |
-0,00724 |
|
|
-28,33 |
-1,0408 |
-0,13763 |
-0,00048 |

 кроку
кроку