5. Опуклі функції і точки перегину

Нехай функція визначена на _.

_{Визначення 2. Кажуть, що є опуклою униз функцією на , якщо для будь-яких двох точок і , які належать графіку функції , дуга, яка з’єднує ці точки, лежить під хордою (рис.3).}

_{Визначення 3. Кажуть, що є опуклою вверх функцією на , якщо для будь-яких двох точок і , які належать графіку функції , дуга, яка з’єднує ці точки, лежить над хордою (рис.4).}

Теорема 4. Нехай функція визначена і диференційована на _{. Для того, щоб була опуклою униз (вверх) на необхідно і достатньо, щоб похідна монотонно зростала (спадала) (не обов’язково строго) на .}

_{Наслідок.} Нехай функція визначена і двічі диференційована на _{. Для того, щоб була опуклою униз (вверх) на необхідно і достатньо, щоб}

_{для .}

_{Визначення 4.} Нехай функція визначена на _{і точка . Нехай існує окіл точки такий, що зліва і справа від точки в цьому околі функція зберігає напрямок опуклості. Якщо ці напрямки різні, то точка називається точкою перегину функції (рис.5).}

_{Теорема 5 (необхідна умова точки перегину функції).} Нехай функція визначена на _{. Якщо точка є точкою перегину функції для , то виконується одна з наступних умов:}

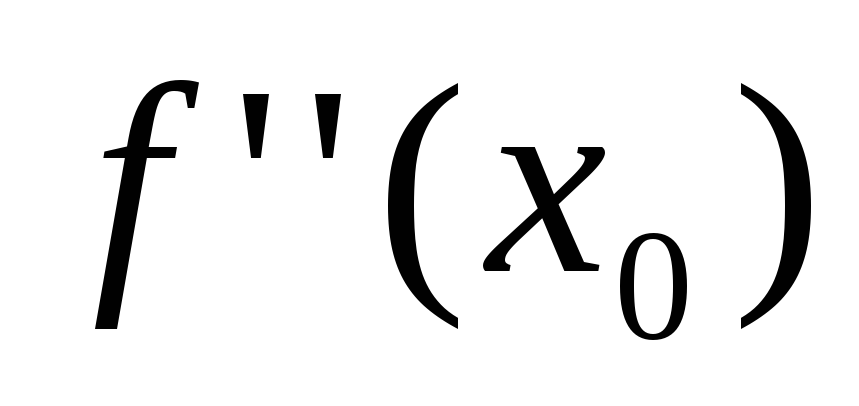• _{не існує;}

• _.

_{Таким чином, точки, підозрілі на перегин, - це точки з , де похідна другого порядку не існує чи дорівнює нулю.}

_{Теорема 6 (достатня умова точки перегину функції).} Нехай функція визначена, двічі диференційована на _{і . Якщо має похідну третього порядку в точці і , то точка є точкою перегину для функції .}

_{Приклад. Знайти точки перегину функції . Область визначення функції: . Спочатку треба знайти точкі, які є підозрілими на пергин. Для цього знайдемо похідну другого порядку:}

_{На області визначення функції немає точок, де не існує. Знайдемо нулі для :}

_.

_{На області визначення функції , тому нуль визначиться тільки завдяки . Таким чином, - єдина точка, підозріла на перегин. Ця точка розділяє область визначення функції на дві множини, де зберігає свій знак, а тому зберігає характер опуклості (див. табл.1).}

_{Таблиця 1 –}

Питання

1. _{Які точки називаються стаціонарними для функції ?}

2. _{Як визначити точки, підозрілі на екстремум для функції ?} Необхідна умова локального екстремума функції.

3. _{Чи завжди для знаходження екстремума функції можна користуватися} першою достатньою умовою?

4. Друга достатня умова локального екстремума.

5. Третя достатня умова локального екстремума.

6. Чи для будь-якої функції можна знайти її найменше і найбільше значення?

7. _{Визначення опуклої униз (вверх) функції.}

8. _{Критерій опуклості функції.}

9. _{Визначення точки перегину функції. Необхідна умова точки перегину функції.}

10. _{Достатня умова точки перегину функції.}