1.6.2. Построение лфчх заданной системы

Для исследования системы на устойчивость по амплитудно-фазовому критерию устойчивости с помощью логарифмических частотных характеристик необходимо кроме ЛАЧХ построить еще логарифмическую фазо-частотную характеристику (ЛФЧХ). По оси абсцисс откладывается частота в логарифмическом масштабе (используют ту же ось частот, что и для построения ЛАЧХ), а по оси ординат откладывают аргумент амплитудно-фазовой характеристики φ(ω) в градусах или в радианах в линейном масштабе. ЛФЧХ  рассчитывается по формуле

Φ_з(ω) = -1,57- arctg(T_уω) - arctg(T_кзω) - arctg(T_дω)

Φ_з(ω) = -1,57 – arctg(0.06ω) – arctg(0.28ω) – arctg(0.027ω)

Ниже приведена таблица для построения ЛФЧХ заданной системы.

	lg()	()
0,0001	-4	-1.57
0,001	-3	-1.57
0.01	-2	-1.574
0.1	-1	-1.607
0.5	-0.3	-1.753
1	0	-1.93
5	0.7	-2.947
5,5	0,75	-3.032
7	0,85	-3.254
10	1	-3.603
20	1.3	-4.337
25	1.4	-4.577
30	1.47	-4.769
35	1,54	-4.925
40	1,6	-5.054

График ЛФЧХ заданной системы приведен в Приложении 4.

Так как ЛАЧХ пересекает ось абсцисс раньше, чем ЛФЧХ пересекает прямую (–) , то заданная система устойчива.

Определяем по графику запас устойчивости по фазе: θ = 31.5º.

1.6.3.Построение желаемой лачх

При построении желаемой ЛАЧХ выделяют три области: область низких частот, область средних частот и область высоких частот. Вид ЛАЧХ в каждой из областей по-разному влияет на качество системы. В области низких частот вид ЛАЧХ определяет точность работы системы в установившихся режимах. Область средних частот определяет динамические свойства системы. Вид ЛАЧХ в области высоких частот практически мало влияет на качество системы.

Последовательность построения желаемой ЛАЧХ:

Таблица 1

ωm, %	10	15	20	25	30	35	40
tpωc/	5	4,4	4	3,6	3,2	3,0	2,8
L1, дБ	18	15	13,5	12	11	10,5	10
θ, гр.	85	80	65	55	45	40	35

1.По таблице 1 определяем tpc/=3,2 , откуда следует

с=3,2/tp=3,2∙3.1416/2=5,027 с^-1 lgc=lg5,027=0,701

Наносим на ось абсцисс частоту среза с и проводим через нее прямую линию с наклоном –20дБ/дек. Частота 2, ограничивающая область средних частот желаемой ЛАЧХ слева определяется величиной отрезка L1=20. Частота 5 ограничивает область средних частот справа.

В области высоких частот желаемая ЛАЧХ строится в виде прямолинейного отрезка с наклоном –80 дБ/дек.

В области низких частот желаемая ЛАЧХ строится следующим образом. По заданной величине коэффициента усиления системы Кс определяем величину LА=20lgКс=20lg100=40 и отмечаем на чертеже точку А с координатами А=1с-1 и LA. Через точку А проводим линию с наклоном -20 дБ/дек. Сопряжение частей характеристики области средних частот и области низких частот проводится прямой линией с наклоном –40 дБ/дек.

В задании на разработку указана максимально допустимая ошибка слежения Хmax при условии, что входной сигнал может изменяться с максимальной угловой скоростью 0max и максимальным угловым ускорением 0max, для выполнения этого требования необходимо, чтобы желаемая ЛАЧХ не попала в запретную область.

Построение запретной области.

Отмечаем на чертеже точку с координатами :

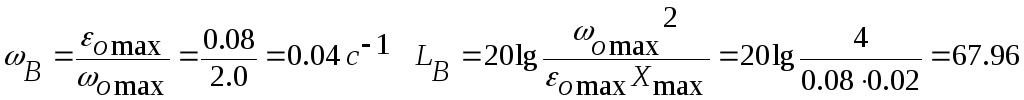
Lg(ω_B)=lg(0.04)=-1.398

От точки В вправо проводим прямую линию с наклоном –40 дБ/дек, а влево – прямую линию с наклоном –20 дБ/дек.

ЛАЧХ, построенная по заданному коэффициенту Кс=100, попадает в запретную область, поэтому для обеспечения заданной точности слежения нужно увеличить коэффициент Кс, т.е. поднять желаемую ЛАЧХ так чтобы она не попадала в запретную область.

По виду желаемой ЛАЧХ (рис.3) записываем передаточную функцию

Исследование системы на устойчивость по амплитудно-фазовому критерию устойчивости с помощью логарифмических частотных характеристик.

_ж()= - 90 – arctgТ₁ - 3arctgT₅ + arctgT₂ =

= - 90 – arctg14.125 - arctg0.027 + arctg0.708 (гр)

Результаты сведены в табл.1

Таблица1.

w	lg(ω)	j(w)
0,0001	-4	-1.571
0,001	-3	-1.583
0.01	-2	-1.704
0.1	-1	-2.462
0.5	-0.3	-2.7
1	0	-2.535
5	0.7	-2.234
5,5	0,75	-2.251
7	0,85	-2.319
10	1	-2.494
20	1,3	-3.122
25	1,4	-3.405
30	1,47	-3.657
35	1,54	-3.88
40	1,6	-4.075

График ЛФЧХ скорректированной системы представлен в Приложении4. Так как ЛАЧХ пересекает ось абсцисс раньше, чем ЛФЧХ пересекает прямую – , то желаемая система устойчива. Определяем по графику запас устойчивости по фазе: θ = 0.55рад или 31,53º

Из графика (рис.3) видно, что система устойчива и запас устойчивости не меньше заданного.