2.2. Апериодическое звено второго порядка
Дифференциальное уравнение звена в операторной форме имеет вид
,
или
,
где = Т1/2T2 > 1 - коэффициент затухания.
Передаточная функция этого звена равна
.
Из последнего выражения видно, что подобное звено может быть представлено как последовательно включенные два апериодических звена первого порядка.
По переходной характеристике можно определить параметры звена следующим образом. В точке перегиба кривой (рис.1.2) нужно провести касательную к кривой и измерить расстояния a, b, c, как показано на рис.1.2. При определении расстояний a и b принять масштаб, соответствующий ууст = 1. Постоянные времени Т3 и Т4 определяются из следующих выражений:
5
Т3
+ Т4
= С, Т3
> T4,
.
Коэффициент усиления равен К = ууст/xуст .
6
Передаточная функция такого управляющего устройства равна
.
(11)
Определим ошибку системы с ПИ-законом управления, для чего подставим в уравнение (2) передаточные функции звеньев (3) и (11). После преобразований получим:
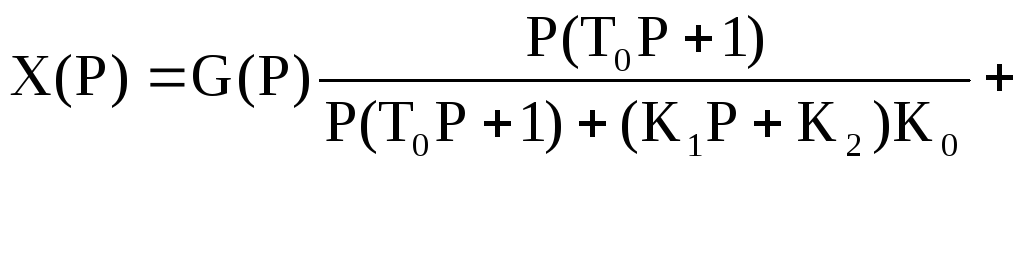
(12)
Из (12) видно, что установившаяся ошибка при постоянных входных сигналах g(t) иf(t), как и при И-законе управления, равна нулю. Однако, динамические свойства у системы с ПИ-законом управления лучше, чем с И-законом (при прочих равных условиях).
По своим свойствам изодромная система в переходном режиме приближается к системе с пропорциональным управлением, а в установившемся режиме подобна системе с интегральным управлением.
2.4. Пропорционально-интегрально-дифференциальное управление (закон пид)
Управляющее устройство вырабатывает сигнал, равный сумме трех составляющих: пропорциональной ошибке, интегралу от ошибки и производной от ошибки
31
Нетрудно видеть из уравнения (8), что в установившемся режиме (Р = 0) при постоянных входных сигналах g(t) иf(t) ошибка равна нулю.
При данном законе управления система является астатической (если возмущение приложено к точке системы, расположенной за интегрирующим звеном, т.е. за регулятором).
Рассмотрим теперь режим работы системы, когда задающее воздействие изменяется с постоянной скоростью, т.е. G(P)P= =V0=const. Подставим в (8)G(P)P=V0:
.
(9)
Установившаяся ошибка в этом режиме работы называется скоростной ошибкой и может быть определена из уравнения (9), если положить Р=0:
.
Коэффициент усиления в такой системе иногда называют добротностью по скорости или просто добротностью.
По сравнению с П-законом И-закон управления обеспечивает астатизм системы, однако динамические свойства системы с И-законом управления обычно хуже, чем у системы с П-законом.
2.3. Изодромное управление (закон пи)
При изодромном законе управления управляющее устройство вырабатывает сумму двух сигналов: пропорционального ошибке и пропорционального интегралу от ошибки
.
30
2.3. Колебательное звено
Дифференциальное уравнение звена имеет такой же вид, как и уравнение апериодического звена второго порядка. Однако коэффициент затухания <1.
Переходная характеристика колебательного звена имеет колебательный характер (рис.1.3).
По переходной характеристике параметры звена можно определить с помощью следующих формул:
.
2.4. Интегрирующее звено
Выходная величина этого звена пропорциональна интегралу от входной величины:
или
Передаточная функция такого звена имеет вид:
-
где
Переходная характеристика звена показана на рис.1.4.
7
2.5. Идеальное дифференцирующее звено
Передаточная функция такого звена имеет вид
W(P) = P .
Если на вход такого звена подать ступенчатое воздействие, то на выходе получится импульс бесконечно малой длительности и бесконечно большой по величине. Никакое реальное звено не может выдать бесконечно большой по величине сигнал. В реальных звеньях всегда проявляется в той или иной степени инерционность.
В некоторых случаях может оказаться, что инерционные свойства реального дифференцирующего звена малы по сравнению с инерционностями других элементов системы. При этом оказывается возможным пренебречь инерционностью дифференцирующего звена и считать его идеальным.