Задания к лабораторной работе
Задание № 1
Выполнить действия над матрицами:
A=
,B=
(четные варианты)
A=
,B=
(нечетные варианты)
-
Вариант
C
1
A(2A+B)-B(A-B)
2
2AB-(A+B)(A-B)
3
2AB-3B(A-B)
4
(3A+B2)5B(A-B)
5
A(A2-B)-A(B+A)
6
3AB+(A-B)(A+2B)
7
A2-(A+B)(A-3B)
8
(A2-B2)(A-B)
9
(A-B2)(2A+B)
10
A(2A+B)-B(A-B)
11
3AB+(A-2B)-A(B+A)
12
(A+2B)(3A-B)
Задание № 2
Решить уравнение XD=R с помощью обратной матрицы.
-
Вариант
D
R
1
2
3
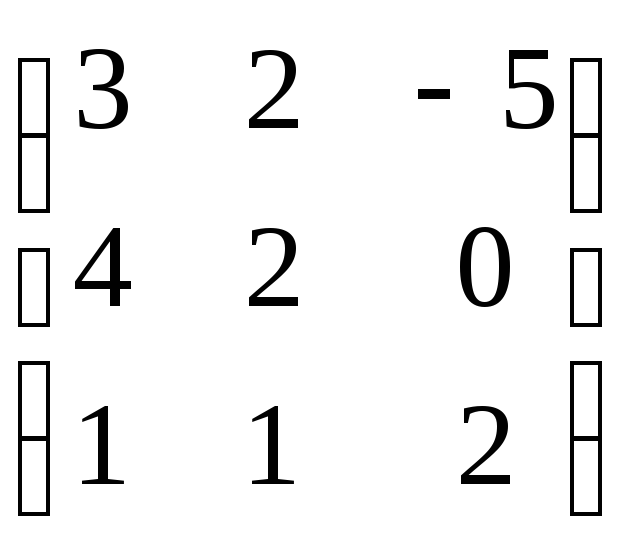
4
5
6
7
8
9
10
11
12
Л.Р. №3. Построение графиков
Основной функцией, обеспечивающей построение графиков на экране дисплея, является функция plot(х, у, s), где х, у – массивы значений аргумента и функции, s – символьная переменная, содержащая 3 спецсимвола: тип линии, тип точки и цвет линии. Значения символьной переменной вы сможете узнать по командеhelp plot.
Например:
1) >> x1 = 0:10;
>> y1 = exp(x1);
>> plot(x1, y1, 'g*-');
Можно отображать на одном графике несколько кривых.
Например:
1) >> x1 = 0:10;
>> y1 =exp(x1);
>> x2 = 1:3:15;
>> y2 = sin(x2+pi/3);
>> plot(x1, y1, 'r*:', x2, y2, 'go-.');
В Matlab существует ряд возможностей редактирования графиков:
– Снабжение графика координатной сеткой – grid.
Например:
>> x = 1:9;
>> y = x.^3;
>> plot(x, y), grid
– Снабжение графика заголовком – title.
Например:
>> x = 1:9;
>> y = x.^3;
>> plot(x, y), grid
>> title('График функции y = x^3');
– Снабжение графика пояснениями, которые размещаются вдоль горизонтальной и вертикальной оси – xlabel,ylabel
Например:
>> x = 1:9;
>> y = x.^3;
>> plot(x, y), grid
>> title('График функции y = x^3');
>> xlabel('value x'); ylabel('value y');
– Размещение текста в поле графика – gtext(место указывается с помощью мыши)
Например:
>> plot(x, y)
>> gtext('FFF')
– Изменение шрифта и размера выводимого текста.
Например:
>> plot(x, y, 'rd-'); grid;
>> title('Graph of y(x)','FontName','Arial','Fontsize',14);
>> xlabel('x'); ylabel('y');
>> gtext({'First line','Second line'},'FontName','Arial','Fontsize',14);
– Создание нового графического окна, оставляя предыдущие – figure.
Например:
>> plot(x, y);
>> figure
>> plot(a, b)
– Отображение в одном графическом окне несколько последовательно вычисляемых графиков – hold on, выключение режима –hold off.
Например:
>> hold on
>> plot(x, y);
>> plot(a, b);
>> hold off
Специальные графики:
1) столбчатая диаграмма – bar
Например:
>> x = 1:10;
>> bar(x)
2) Если функция задана своими значениями при дискретных значениях аргумента и неизвестно, как она может изменяться в промежутках между значениями аргумента, удобнее представлять график такой функции в виде отдельных вертикальных линий для каждого из заданных значений аргумента – stem (символьный параметр задается аналогично, как и вplot).
Например:
>> x = 1:10;
>> stem(x, 'k'),grid
3) Построение графика гистограммы заданного вектора – hist
Например:
>> y = [10 3 7 11 5 6 1 0 9];
>> hist(y)
4) Построение графика в виде траектории кометы – comet.
Например:
>>t = 0:0.1:50;
>> x = 4 * exp(-0.05*t) .* sin(t);
>> y = 0.2 * exp(-0.1*t) .* sin(2*t);
>> comet(x, y)
5) Построение графиков в логарифмическом
масштабе – logspace(d1,
d2, N)формирует вектор-строку, содержащую
N равноотдаленных в логарифмическом
масштабе друг от друга точек, которые
покрывают диапазон от
до
;loglog– построение
графика в логарифмическом масштабе.
Например:
>> x = logspace(1, 3);
>> y = 1 ./ x;
>> loglog(x, y)
Дополнительные функции графического окна.
В Matlab существует возможность определения разных режимов масштабирования. Это достигается за счет использования процедуры axis. Сведения о параметрах этой процедуры вы можете узнать поhelp axis.
Например:
1) >> x = 1000: 10: 1500;
>> y = x ./ 10;
>> axis([1000 2000 100 200]);
>> plot(x, y)
В одном графическом окне, но на отдельных графических полях можно построить несколько графиков. Для этого используется процедура – subplot(m,n,p),m– указывает, на сколько частей делится графическое окно по вертикали;n– по горизонтали;p– номер подокна.
Например:
1) >> x = 1:2:10;
>> y = exp(x);
>> a = 4:4:49;
>> b = a.^2 / 2;
>> subplot(2, 1, 1)
>> plot(x,y);
>> subplot(2,1, 2)
>> plot(a, b)