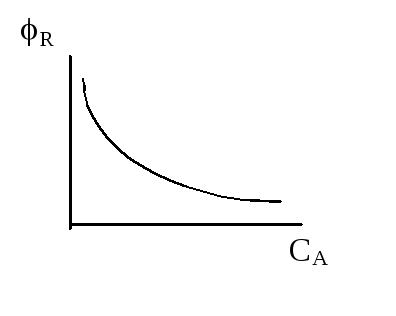
Селективность различных реакций

n1 и n2	WR/WS	φR = f(CA)	φR = f(XA)	рекомендуемый тип реактора
n1 > n2 n1 - n2 = a				РИВ
n1 < n2 n1 - n2 = - a				РИС - Н
n1 = n2 n1 - n2 = 0		Не зависит от СА и ХА		Любой

Последовательные реакции

Ограничимся случаем реакций первого порядка, протекающих без изменения объема. Кинетические уравнения будут

1)

2)

3)

Первое уравнение описывает скорость расходования вещества А. Второе - результирующую скорость накопления продукта R. Если целевой продукт – R, то соотношение скоростей образования R и S будет

Уравнение показывает, что селективность будет тем больше, чем выше концентрация исходного реагента и соотношение k₁/k₂ .

Зависимость селективности от степени превращения

Для элементарного объема РИВ для реакции

,

протекающей без изменения объема cмеси и при равенстве a = r = s селективность будет

Выход продукта Ф или Χ

В РИС - Н эта зависимость

Зависимость селективности от степени превращения позволяет выбрать оптимальную модель реактора для максимального выхода целевого продукта.

Следовательно, при проведении последовательных реакций более высокая селективность достигается в РИВ и РИС – П.

Селективность также зависит от соотношения k₁ / k₂ .

Если константа скорости второй реакции k₂ значительно больше первой k₁ (k₂ >> k₁), высокая селективность достигается только при малых степенях превращения и резко падает при высоких степенях превращения. Для получения высокой селективности такие процессы следует осуществлять по циклической схеме при малой степени превращения исходного сырья за один проход через реактор. Целевой продукт извлекается из реакционной смеси с последующей рециркуляцией непрореагировавшего сырья.

Если k₂ << k₁, можно одновременно достичь высокой селективности и степени использования сырья без введения рецикла.

Селективность процесса по промежуточному продукту при последовательной реакции

Зависимость селективности от степени превращения для необратимой реакции

Выход целевого продукта, селективность и степень превращения зависят от модели реактора. Если селективность с увеличением степени превращения уменьшается (а, б), выход будет уменьшаться. В этом случае площадь под кривой больше площади прямоугольника, поэтому предпочтительнее РИВ и РИС – П. К – РИС занимает промежуточное положение.

Если с увеличением степени превращения селективность возрастает, то лучше использовать РИС – Н. В этом случае применение каскада не рекомендуется, т. к. выход в нем будет ниже, чем в единичном реакторе.

Химические реакторы с неидеальной структурой потока

Рассмотрим одну из важнейших особенностей, присущий большинству химико-технологических процессов и очень что редко встречаются в «чистой» химии, а именно поток. Он характерный для подавляющего большинства технологических аппаратов: вносит в них исходные вещества, переносит реакционную смесь от входа до выхода, выносит продукты из аппарата. Поток сыграет важнейшую роль в процессах переноса тепла и вещества. Эти процессы также чрезвычайно специфические для химической технологии и в то же время их довольно редко приходится учитывать в лабораторных химических экспериментах.

Итак, поток. Течь может газ (например, смесь азота с водородом при синтезе аммиака), жидкость (течение мономеров при полимеризации в потоке), движение шихты в доменной печи тоже можно рассматривать как поток. Могут быть и значительно больше сложные случаи, когда «течет», двигается многофазная смесь типа суспензии или эмульсии или когда в аппарате организуют два потока навстречу друг другу (например, газ поднимается вверх, а навстречу стекает жидкость) и т.д. Будем рассматривать в основному движение одного потока; при этом для простоты все, что течет, будем называть жидкостью - будь то жидкость, газ или, например, суспензия. Лишь в отдельных случаях будут даваться уточнение, о котором именно потоке речь идет.

Главная роль потока в химическом процессе — это перенос: перенос реагирующей массы вдоль аппарата, перенос тепла, которое выделяется в процессе, из глубины аппарата к охлаждающим стенкам и т.д. При этом наиболее важные два аспекта: перенос в продольном направлении (в том направления, куда двигается поток, а также в противоположном — навстречу потоке) и перенос в поперечном направлении. Эти случаи часто сыграют разную роль, и о них следует поговорить отдельно.

Прежде чем говорить о переносе в потоке отметим что, большинство процессов, которые протекают в реальных условиях, носит сложный характер: каждый процесс состоит из ряда стадий, которые происходят в нем или последовательно, или параллельно. Чаще всего оказывается, что одна из стадий лимитирует процесс. Это значит, что характер протекания процесса в целом определяется данной стадией. Отсюда следует, что интенсификация других (нелимитирующих) стадий слабо влияет на общий ход процесса. Если мы хотим ускорить процесс, необходимо влиять именно на стадию, которая лимитирует. Если стадии процесса последовательные, то лимитировать будет, как правило, самая медленная, самая продолжительная, наименее интенсивная стадия. Если стадии параллельные, то лимитирует быстрейшая, интенсивная, самая мощная стадия.

Рассмотрим пример потока, относя­щийся к иному типу процессов. Завод получает рудный концентрат с обогати­тельной фабрики рудника. Основной спо­соб доставки — железная дорога. Пере­возка складывается из следующих после­довательных стадий: 1) погрузка кон­центрата в вагоны (около 3 часов); 2) следование состава от рудника до завода (около 2 суток); 3) разгрузка (около 4 часов). Вторая стадия — самая длительная и потому лимитирующая. Так, если ускорить в 1,5 раза первую стадию, то время перевозки в целом со­кратится на 1,8 %; если третью — пе­ревозка ускорится на 2,4 %. Если же удастся ускорить в 1,5 раза вторую стадию, то время всей перевозки сокра­тится на 29 %.

С другой стороны, небольшая часть концентрата доставляется не по желез­ной дороге, а автотранспортом. В таком случае оба способа доставки являются параллельными стадиями. Если, напри­мер, автомобильные перевозки в общей сумме составляют 1,5 %, то лимитирую­щей оказывается более производитель­ная стадия — доставка по железной дороге. Вряд ли стоит вкладывать круп­ные средства, чтобы вдвое увеличить автоперевозку, поскольку в итоге это даст лишь незначительный эффект.

В дальнейшем нам неоднократно при­дется выделять лимитирующие стадии и в последовательных, и в параллельных вариантах.

МЕХАНИЗМЫ ПЕРЕНОСА

Структура потока тесно связана с ме­ханизмами переноса. В потоке происхо­дит перенос многих субстанций, но для химической технологии наиболее важны три из них: перенос импульса (количества движения), перенос тепла и перенос вещества. Эти процессы происхо­дят во многом аналогично, и каждый из них может осуществляться тремя раз­личными механизмами, которые регла­ментируются уровнем (масштабом) эле­ментарного акта.

Нижний уровень переноса — кван­товый. Перенос осуществляется путем излучения и поглощения элементарных частиц. Обычно этот механизм так и на­зывают излучением (лучистым перено­сом). Так может переноситься импульс (вспомните давление света); именно та­ким образом тепло Солнца передается нам на Землю; так переносится и ве­щество (в космических лучах, в потоках элементарных частиц, летящих из выход­ных устройств ускорителей, и т. д.). Мы почти не будем касаться лучистого переноса, поскольку в «обычной» химической технологии его роль не очень значительна, и только лишь в области высоких температур излуче­ние тепла начинает определять особен­ности процесса. Следующий уровень — молекуляр­ный: перенос происходит в результате теплового движения молекул. Процессы молекулярного переноса называются по-разному. Перенос импульса на молеку­лярном уровне называют вязкостью (вязким трением). Мы все в общем представляем себе, что такое вязкость, но почему вязкость — это перенос импуль­са, понять не столь легко.

Представим себе две параллельные линии рельсов (рис. 1, а). На одной стоит неподвижная платформа Б, по другой движется платформа А. На обеих плат­формах стоят люди. В момент, когда обе платформы поравнялись, люди с платформы А перепрыгивают на плат­форму Б, а с Б на А. Что произой­дет? Человек, перепрыгивающий с движу­щейся платформы на неподвижную, участвует в двух движениях: попереч­ном — с платформы на платформу, и продольном — вместе с платформой, от которой он отталкивается. После «при­земления» он передаст неподвижной платформе продольный компонент им­пульса: она получит толчок вперед. На­оборот, человек, прыгающий с неподвиж­ной платформы на движущуюся, подтор­маживает ее. После перепрыгивания лю­дей платформа А будет двигаться мед­леннее, чем до этого, а платформа Б придет в движение (рис. 1, б). Пере­прыгивающие люди перенесли импульс.

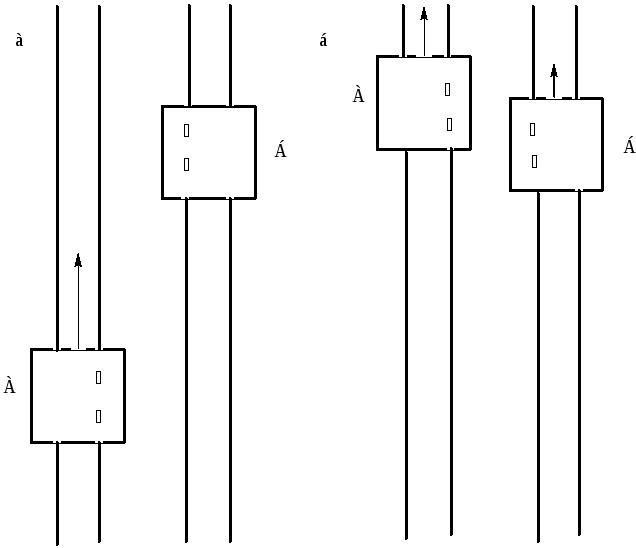
Рис. 1.

Обратимся теперь к другой (тоже упрощенной) схеме. Представим себе две массы газа, разделенные плоскостью, сквозь которую молекулы газа могут свободно пролетать. В начальный мо­мент одна масса неподвижна, другая движется вдоль плоскости раздела. Вследствие теплового движения молеку­лы будут перелетать из движущейся части в неподвижную, перенося свою порцию продольной составляющей импульса, и из неподвижной части в движу­щуюся, подтормаживая ее. Таков меха­низм вязкого трения в газах, заключаю­щийся в переносе импульса в направ­лении, перпендикулярном направлению движения. (В жидкостях механизм пере­носа импульса несколько сложнее, так как он связан не только с перелетом молекул. В этом случае молекулы взаи­модействуют значительно сильнее, чем в газе, и заметная доля импульса переда­ется от молекулы к молекуле; но смысл вязкого трения как поперечной передачи импульса сохраняется и здесь.) Заметим, что, описывая движения газа, мы на са­мом деле говорили о двух очень разных движениях. Первое — это тепловое движение молекул. Второе — это движе­ние газа как такового; часто его назы­вают массовым движением или тече­нием. В текущем газе молекулы пере­мещаются в самых разных направлениях, и лишь в среднем число молекул, имею­щих скорость в направлении течения, превышает число молекул, движущихся в иные стороны.

Теперь рассмотрим молекулярные ме­ханизмы переноса тепла и вещества. Перенос тепла на молекулярном уровне называется теплопроводностью, а пере­нос вещества — диффузией.

Перенос тепла может осуществляться двояко: либо молекулы, обладающие бо­лее высокой энергией (которая соответ­ствует более высокой температуре), пе­ремещаются с места на место, пере­нося таким образом тепловую энергию, либо эти молекулы (назовем их «горя­чими»), сталкиваясь с другими, «холод­ными» молекулами, передают им свою энергию — в этом случае тепло передает­ся как бы эстафетой. Перенос вещест­ва диффузией обязательно связан с непо­средственным перемещением молекул. Здесь эстафетный механизм, разумеется, невозможен — чтобы данное вещество переместилось, должны переместиться именно его молекулы. Мы уже говорили об аналогии меж­ду процессами переноса. На молекулярном уровне эта аналогия имеет четкое количественное выражение. Если в на­правлении х происходит перенос импуль­са, тепла или вещества, то поток q дан­ной субстанции (количество импульса тепла, вещества, переносимое в единиц) времени через единицу площади поперечного сечения) определяется следующим} выражениями:

для импульса (1)

для тепла Q (2)

для массы вещества m (3)

В этих уравнениях символом —обоз­начены производные соответствующих функций по координате х; — ком­понента скорости, перпендикулярная оси х (вспомним, что перенос импульса про­исходит в направлении, перпендикуляр­ном направлению движения); Тис — температура и концентрация вещества; и μ, λ и D — коэффициенты, характе­ризующие интенсивность процессов мо­лекулярного переноса, которые называют соответственно коэффициентами дина­мической вязкости, теплопроводности и диффузии.

Уравне­ния(1) — (3) совершенно одинаковые, только буквенные обозначения раз­личаются. Здесь хотелось бы отметить одну исключительно важную особенность математики, о которой прекрасно сказал великий французский математик А. Пу­анкаре: «Математика — это искусство называть разные вещи одинаковыми име­нами». Что же дает это искусство в данном случае?

Если коэффициенты в уравнениях численно равны, то и решения окажут­ся одинаковыми. В ряде случаев карти­ны распределения в пространстве скорос­ти, температуры и концентрации оказы­ваются идентичными. По полю темпера­туры можно судить о поле концентра­ций; воздействуя на распределение ско­рости, мы одновременно воздействуем на распределение температур.

Глубина и точность аналогии между процессами переноса импульса, тепла и вещества определяются соответствием между коэффициентами.

Не вдаваясь в подробности теории вопроса, но тем не ме­нее отметим, что сравнивать в действи­тельности приходится не коэффициенты μ, λ и D, а величины ν= μ/Q, а= λ /(χ •ρ) и D (здесь ρ — плотность вещества, а χ — его теплоемкость).

В газах интенсивность всех трех ти­пов молекулярного переноса почти оди­накова. Поэтому та аналогия, о которой мы говорим, в газах проявляется наибо­лее полно, и коэффициенты ν , а и D ред­ко различаются больше чем в 1,5 раза. При этом указанные соотношения выпол­няются тем лучше, чем меньше газ от­личается от идеального.

В жидкостях различие уже намного заметнее, здесь обычно ν >а>>D. Это свя­зано с тем, что перенос импульса и тепла в значительной мере происходит по «эстафетному» механизму, а перенос вещества — нет. Наконец, в твердом веществе коэффициент ν очень велик, коэффициент а значительно меньше, но тоже велик, а коэффициент D близок к нулю. Поэтому, например, внутри по­ристого тела перенос тепла и вещества, будут происходить существенно по раз­ному: вещество будет диффундировать по порам, а тепло в основном переда­ваться по твердому материалу, образую­щему стенки пор.

Теперь перейдем к высшему уровню переноса — этот уровень определяется массовым движением (потоком) жидкос­тей, газов, твердых тел. Двигаясь, по­ток переносит с собой и импульс, и тепло, и вещество. Такой перенос на­зывается конвективным (конвекцией).

Главная отличительная черта конвек­ции — большая мощность. Перемещение даже очень малых количеств жидкости или газа переносит много больше им­пульса, тепла и вещества, чем пере­мещение молекул под действием тепло­вого движения. Это связано с тем, что молекулы очень малы. Перемещение даже малых масс жидкостей переносит огромное их количество, что и обуслов­ливает большую мощность конвективно­го переноса.

Вспомним, что мы говорили о лими­тирующих стадиях. Практически всюду, где параллельно перенос может осущест­вляться и конвекцией, и молекулярными механизмами, лимитирует конвективный перенос.

Для того чтобы рассчитать количест­во тепла, передаваемого в нашу квар­тиру, мы определим, сколько его несет поток горячей воды из бойлерной. При этом никому не придет в голову учи­тывать еще то тепло, которое будет в то же самое время передаваться по воде и по стенкам труб теплопроводностью: его количество ничтожно мало. Но обратим внимание вот на что. Тепло это было бы для нас абсолютно бесполезным, если бы в радиаторах оно не выходило из теку­щей воды наружу, в комнаты. Вот здесь есть важная тонкость. По трубам тепло движется в направлении потока (мы назвали это направление продольным), а переход из радиатора в комнату осу­ществляется поперек потока. Для даль­нейшего важно разобраться в картине поперечного переноса, с которым связан не только выход тепла или вещества из потока наружу, но и характер само­го потока.

СТРУКТУРА ПОТОКА И ПОПЕРЕЧНЫЙ ПЕРЕНОС

Начнем с упрощенной схемы. Пред­ставим себе дорогу, идущую под уклон. При этом вся дорога состоит из серии параллельных неглубоких желобков. По желобкам катятся шарики. По бокам дороги — крутые стенки, так что шарики вылететь с нее не могут. Пока уклон невелик, невелика и скорость, и каж­дый шарик катится по «своему» желоб­ку. Все они движутся параллельно друг другу. Эта картина соответствует тече­нию жидкости при малых скоростях: каждая частица жидкости движется па­раллельно другим. При этом обнаружи­вается одна особенность, которую не мо­жет передать наша модель «шарики в желобках». Непосредственно у стенки скорость жидкости равна нулю. Жид­кость как бы «прилипает» к стенке. Этот факт — нулевая скорость у стен­ки — подтверждается бесчисленными измерениями, причем, как ни удивитель­но, падение скорости до нуля происходит независимо от материала стенки и от того, какая жидкость (или газ) течет.

Но раз это так, то в попереч­ном направлении существует градиент скорости, и в соответствии с уравне­нием (1) импульс будет переноситься от оси потока к стенке. Количественное рассмотрение этого переноса приводит к такому выводу.

В простейшем случае (поток в круг­лой трубе) скорость максимальна на оси трубы; здесь она в 2 раза больше, чем средняя скорость потока. Далее к стенкам скорость падает до нуля, и ха­рактер ее изменения описывается

парабо­лой. При этом во всех точках, равно­удаленных от оси, скорость одинакова. Частицы, находящиеся на равном рас­стоянии от оси, образуют цилиндриче­ский слой, движущийся с постоянной скоростью. Слои, более близкие к стен­кам, движутся медленнее, а более близ­кие к оси — быстрее. Такое тече­ние называют ламинарным (от латинского lатiпа — пластина, слой).

В конце концов, импульс, переноси­мый от оси к стенке, передается этой стенке. При этом происходит рассеяние энергии. Таким образом, описываемая передача импульса может рассматриваться как трение, на преодоление ко­торого нужно затрачивать энергию, т. е. речь идет о так называемом гидравли­ческом сопротивлении.

Теперь снова вернемся к шарикам, катящимся по желобкам. Пусть уклон дороги возрос, т. е. возросла и скорость. Тогда малейшая неровность одного из желобков приведет к тому, что шарик вылетит из него и перелетит в другой желобок. При этом он, вероятно, выбьет из этого желобка тот шарик, который там находился. Кроме того, и по этому желобку шарик прокатится недолго: лю­бая помеха, неровность — и шарик опять срывается со своей траектории и переле­тает в какой-то еще желобок. Через некоторое время картина будет такой: все шарики в беспорядке то движутся по каким-либо желобкам, то переле­тают из одного желобка в другой.

Так и с жидкостью. Если начать уве­личивать скорость, то в какой-то момент ламинарное течение станет неустойчи­вым. При любом возмущении («неров­ности желобка») частица сойдет со сво­его места в «строю» (в соответствую­щем цилиндрическом слое) и двинется куда-то в сторону, «расталкивая» те час­тицы, которые движутся там. Но ведь пространство трубы заполнено жид­костью, и если одна частица смести­лась, то не на свободное место, а на позицию, которая ранее была занята. Таким образом, в беспорядочное, хаоти­ческое движение окажутся вовлеченными многие частицы, а затем и весь поток.

Теперь картина потока иная. Жид­кость по-прежнему движется вдоль тру­бы. Но на это "движение накладывают­ся хаотические колебания (пульсации, флуктуации), происходящие в различных направлениях. Такой поток называют турбулентным (от латинского turbulentus — беспорядочный). Вы многократ­но сталкивались с этим явлением. По­лоскание флага на ветру или ветер, ко­торый то и дело меняется перед пере­меной погоды,— вот два проявления турбулентности атмосферы. В общих чер­тах турбулентный поток «устроен» сле­дующим образом. В текущей жидкости выделяются области, каждая из которых в данный момент движется приблизи­тельно как единое целое. Приблизитель­но, потому что все время происходит взаимное перемещение более мелких ча­стей этой области, причем в основном оно носит вихревой характер. Каждая такая область (частица) завихрена, по^: этому их часто так и называют — вихри.

Типичный пример турбулентного вих­ря — атмосферный циклон, представляю­щий собой весьма внушительный вихрь: масса воздуха, переносимая в нем, мо­жет составлять миллиарды тонн; но и это явно не предел. Солнечные пятна — тоже вихри в турбулентной атмосфере Солнца, вихри, по сравнению с которыми Земля — как горошина рядом с речным водоворотом. И пожалуй, каждая галак­тика тоже может рассматриваться как вихрь в турбулентной Вселенной.

Вихрь в потоке (не будем говорить о галактиках) существует недолго. Тур­булентные пульсации «растаскивают», разрывают его на более мелкие вихри, те, в свою очередь, распадаются на еще более мелкие. Но параллельно образуют­ся новые большие вихри, и вся эта слож­ная картина многократно повторяется.

Может возникнуть вопрос: а разве в ламинарном потоке нет возмущений? Неужели там уж все так гладко? Воз­мущения, конечно, есть. Но вспомним нашу модель — дорогу с желобками. Пока скорость была невелика, возмуще­ния гасили стенки желобка. В ламинар­ном потоке эту роль играет вязкость. «Возмутившаяся» частица отдает изли­шек импульса окружающим, те — даль­ше, и опять они движутся, «как все». Когда же скорость (и импульс) растет, сил вязкости уже не хватает, чтобы удер­жать частицу «в желобке». Возникает турбулентность. Поэтому условия пере­хода от ламинарного режима к турбу­лентному определяются соотношением между скоростью и вязкостью. Мерой этого соотношения является число Рейнольдса, или критерий Рейнольдса,— ве­личина, названная в честь О. Рейнольд­са, замечательного английского ученого, около 200 лет назад впервые изучившего переход из ламинарного режима течения в турбулентный. Число Рейнольдса Rе имеет вид:

,

где ω— скорость, d — размер, ха­рактеризующий данный поток, ρ и μ — соответственно плотность и вязкость жидкости. Если поток движется в трубе круглого сечения и d — ее диаметр, то при Rе<2320 устойчивым будет ла­минарный режим, при Rе>10 000 — турбулентный, а в промежутке будет наб­людаться переменный режим. Правда, если трубу тщательно отполировать, что­бы исключить возмущения, то удается продлить область ламинарности до зна­чительно больших значений Rе, но ма­лейшая встряска — и наступает турбу­лентный режим.

Важнейшая для химической техноло­гии особенность турбулентного потока — это характер процессов переноса в нем. Представим себе ламинарный поток на грани перехода в турбулентный. Пусть в результате возмущения одна из ча­стиц, движущаяся вдоль оси трубы (и по­этому имеющая максимальную ско­рость), начинает смещаться к стенке. При этом она переносит в периферий­ную зону потока свою большую продоль­ную составляющую импульса. Вдобавок, как сказано выше, она вытеснит более медленную частицу, которая будет сме­щаться ей навстречу, перенося свой ма­лый импульс и уменьшая скорость осевой части потока. Скорости будут выравни­ваться по сечению.

Ясно, что описанная картина вырав­нивания скоростей аналогична картине переноса импульса механизмом вязкости. Разница лишь в том, что здесь пере­нос — конвективный (переносят импульс не молекулы, а частицы, состоящие из огромного числа молекул), и поэтому его мощность неизмеримо выше. Если выразить закономерности переноса урав­нением (1), то коэффициент окажется очень большим. Теперь это уже не мо­лекулярная вязкость μ, а турбулентная вязкость μ_т, обусловленная турбулентны­ми пульсациями. В соответствии с большой величиной (μ_т производная в правой части уравнения (1) должна быть мала (иначе произведение дало бы нереальное значение потока ρ_тω)- Это значит, что наклон кривой, изображающей распреде­ление скорости по поперечному сечению, мал. Это уже не парабола, а очень пло­ская кривая, так как перемешивание ча­стиц выравнивает скорости.

Наряду с турбулентной вязкостью можно говорить о турбулентной тепло­проводности и турбулентной диффузии. Турбулентность интенсивно перемеши­вает жидкость в поперечном направле­нии, перенося тепло и вещество, вырав­нивая температуру и концентрации всех веществ. Именно поэтому для химиче­ской технологии типичны турбулентные потоки, а турбулизация — один из важ­ных приемов интенсификации процессов.

Рис.2 Схема потока направленного на стенку

Но картина турбулентного потока по­ка не полна. Необходимо рассмотреть еще одну важную его особенность: по­ведение потока у стенок. Здесь опреде­ляющую роль играют два обстоятель­ства. Во-первых, у самой стенки скорость и в турбулентном потоке тоже падает до нуля; во-вторых, если направить по­ток прямо на поверхность твердого тела (например, пустить из сопла струю воз­духа, как показано на рис. 2), то он не дойдет до поверхности, а «расплю­щится» и начнет обтекать тело. То же самое происходит с турбулентными пуль­сациями. Они не способны дойти до са­мой стенки и вблизи от стенки повора­чивают и начинают двигаться вдоль нее. В результате турбулентный перенос за­тухает. В непосредственной близости от стенки образуется тонкий (так называе­мый пограничный) слой, где перенос осу­ществляется в основном за счет молеку­лярного механизма*.(* Описанная здесь картина упрощена. Сам по­граничный слой обладает сложной структурой, и молекулярные механизмы лимитируют процесс только в части его — подслое. Но для нашего изложения это несущественно) Основную часть по­тока, за вычетом пограничного слоя, обычно называют ядром.

Перенос импульса в пограничном слое осуществляется молекулярной вяз­костью. Так как μ<<μ_T, градиент скоро­сти здесь велик: скорость резко падает от большого значения, существующего в ядре, до нуля у стенки.

То же самое происходит с перено­сом тепла и вещества. В ядре потока температура и концентрации выровнены турбулентным перемешиванием, а в по­граничном слое происходит резкое изме­нение этих величин. Дальше мы в основ­ном будем говорить о переносе вещест­ва, который наиболее специфичен для химико-технологических процессов. Рассмотрим поток, в котором движет­ся раствор какого-либо вещества, при­чем на стенках это вещество расходуется (например, кристаллизуется или всту­пает в реакции). Тогда профиль кон­центраций будет таким, как изображено на рис. 3.

Точное описание изображенной на рисунке картины потребовало бы слож­ного количественного анализа механиз­мов переноса в турбулентном потоке и в пограничном слое. К сожалению, стро­гая теория турбулентного потока до сих пор не создана, поэтому при анализе процессов пользуются теми или иными упрощенными моделями.

Разберем простейшую модель. Ее предложил выдающийся немецкий физико-химик В. Нернст. Нернст, рассматривая процессы растворения твердых веществ и изучая скорость растворения, пришел к выводу, что процесс можно описать следующей схемой. В ядре потока кон­центрация растворяемого вещества рас­пределена равномерно благодаря интенсивному перемешиванию. Но у поверхно­сти твердого тела существует как бы неподвижная пленка, через которую рас­творяемое вещество диффундирует в ядро. Пользуясь современными представ­лениями, естественно сопоставить эту пленку с пограничным слоем. Разумеется, жидкость в нем движется, но для схемы Нернста это не важно. Важно, что пере­нос здесь происходит на молекулярном уровне. Правда, в действительности все гораздо сложнее. Если воспользоваться схемой Нернста (пленочной моделью), то распределение, показанное на рис. 3, преобразуется в картину, изображенную на рис. 4; в ней «срезаны» все закруг­ления, в ядре — полная равномерность, пленка четко отграничена от ядра. В реальном же потоке ядро постепенно переходит в пограничный слой, причем как толщина слоя, так и характер пе­рехода зависят от степени развития тур­булентности. Но для качественного опи­сания пленочная модель оказалась на­столько удобной, что ею широко поль­зуются до сих пор.

Рассмотрим в рамках пленочной мо­дели уравнение (3). Если в пленке не идет реакция, то вещество там не рас­ходуется и не образуется, поэтому по­ток ц не меняется с расстоянием: сколь­ко вещества вошло в пленку с одной стороны, столько же выйдет с другой. Но тогда правая часть уравнения по­стоянна, и в этом случае производная просто равна разности концентраций с разных сторон пленки, деленной на толщину пленки δ: q_m=D(c₂-c₁)/δ. Это уравнение легко привести к виду:

q_m=β∆c, (4)

где ∆с — разность концентраций между ядром потока и стенкой (ее обычно на­зывают движущей силой массоотдачи); β — коэффициент массоотдачи. Уравне­ние (4) — основная формула, по ко­торой рассчитывают процессы переноса вещества; в нем

β = D /δ (5)

Так же получается уравнение пере­носа тепла (а — коэффициент тепло­отдачи) :

д_я=аАТ. (6)

Влияние потока отражается на вели­чинах β и а, которые определяются тол­щиной пограничного слоя δ. Чем быст­рее поток, чем больше число Рейнольдса, тем сильнее развита турбулентность турбулентные пульсации подходят ближе к поверхности, т. е. δ уменьшается, β и а растут.

Обратите внимание на следующее В ядре потока действуют и конвекция и молекулярные механизмы. Но когда мы обсуждали выравнивание концентраций (скоростей, температур) в ядре, мы го­ворили только о турбулентном перемеши­вании, о конвекции. Это потому, что оба механизма здесь действуют параллельно и лимитирует более мощная конвекция

Если же рассмотреть поперечный пе­ренос в целом, то процесс распадается на две последовательные стадии: вна­чале перенос в ядре, затем — через пограничный слой (если перенос идет от стенки, то пограничный слой — внача­ле, но это не принципиально). Раз ста­дии последовательны, то лимитирует мед­ленная, т. е. перенос в пограничном слое. И воздействовать надо именно на этот слой — только так можно существенно ускорить процесс.

Как же это делается? Главный спо­соб интенсификации — увеличение ско­рости потока. Почему мы мерзнем на ветру? Потому, что через тонкий погра­ничный слой интенсивно теряется тепло На том же ветру быстро сохнет белье, ибо одновременно растут скорости от­дачи и тепла, и влаги.

В химической технологии есть две большие группы процессов, по существу сводящихся к переносу. Это теплообменные процессы (нагревание или охлаждение) и массообменные процессы. Набор массообменных процессов чрезвычайно широк. Это поглощение веществ из газа жидкостью (абсорбция); поглощение из газов или жидкостей поверхностью твер­дых тел (адсорбция); перегонка жидко­стей; выделение веществ из растворов путем растворения в другой жидкости (экстракция). Сюда же относятся рас­творение, кристаллизация, сушка.

В этих процессах почти всегда уве­личение скорости потока приводит к ин­тенсификации переноса вещества. В большинстве современных типов мас­сообменных и теплообменных аппаратов создаются высокие скорости потоков. Но такая интенсификация даром не дается. Чем больше скорость, тем выше гидрав­лическое сопротивление, тем больше по­тери энергии. Значительные усилия кон­структоров направляются на создание таких аппаратов, где сопротивление сни­жено.

В некоторых случаях интенсифициро­вать поперечный перенос тепла и вещест­ва удается не за счет повышения ско­рости, а путем создания особой конфигу­рации поверхности, вдоль которой дви­жется поток.

ПЕРЕНОС ВЕЩЕСТВА И ХИМИЧЕСКАЯ РЕАКЦИЯ

Любая химическая реакция приводит к тому, что вещество либо расходует­ся, либо образуется. Поэтому нужно под­водить реагенты в зону реакции и от­водить из нее образующиеся вещества (продукты). В этом одна из главных функций потока. Если реакция гомоген­ная, т. е. проходит в объеме текущей жидкости, то, как правило, поток справ­ляется со своей ролью.

Но далеко не все реакции проходят в объеме одной движущейся жидкости (или газа). В технологии чаще встре­чаются реакции гетерогенные. Гетероген­ные реакции имеют несколько вариан­тов, важнейшие из которых два. Пример первого варианта — поглощение диокси­да углерода щелочным раствором. В этом случае реакция проходит в жидкости, в ней. же с самого начала находится один из реагентов (щелочь).. Другой же реагент (СО₂) должен прежде чем всту­пить в реакцию, перейти из газа в жидкость (из одной фазы в другую). При этом молекулы СО₂ дважды про­ходят пограничные слои: в газе у гра­ницы с жидкостью и в жидкости у гра­ницы с газом. Пограничные слои воз­никают на границе фаз — именно на­личие этой границы и определяет спе­цифику гетерогенного процесса.

Второй вариант гетерогенных процес­сов не менее важен. Это случай, когда движется только одна фаза (чаще всего газ), а вторая фаза твердая. Но реак­ция происходит не в объеме газа, а на границе — на поверхности твердого тела. Прежде всего так идут гетерогенно-каталитические реакции, протекающие на поверхности твердого катализатора. Мо­лекулы реагентов, прежде чем вступить в реакцию, должны продиффундировать через пограничный слой у твердой по­верхности. Бывают и некаталитические реакции того же типа, например, горе­ние твердого топлива, когда реакция идет на границе топлива с воздухом.

Общая черта гетерогенных реакций заключается в необходимости подвода вещества в зону реакции через погра­ничный слой. Если рассмотреть путь от­дельной молекулы, вступающей в реак­цию, то он складывается из ряда по­следовательных стадий: диффузия к по­верхности (или из одной фазы в другую), реакция, затем часто и обратная диф­фузия продуктов реакции. Мы уже не в первый раз сталкиваемся с такой си­туацией, и поэтому становится ясным, что общая затрата времени на все ста­дии будет больше, чем на какую-либо одну. Значит, скорость суммарного про­цесса окажется меньше скорости одной стадии. Говорят: диффузия тормозит хи­мическую реакцию, и все явление в це­лом называют диффузионным торможе­нием. Ясно должно быть и еще одно. Если одна из стадий много медленнее остальных, она станет лимитировать весь процесс.

Как это происходит, разберем на про­стом примере необратимой реакции, про­ходящей на поверхности катализатора. При этом поверхность омывается пото­ком газа. Одно из современных направлений хи­мии, изучающего скорость химических реакций в условиях, когда на нее влияют процессы переноса тепла и вещества. Это направление называют макрокине­тикой.

Итак, вещество А превращается в ве­щество В по реакции А—>-В. Реакция идет на поверхности катализатора. Ско­рость реакции ω пропорциональна кон­центрации с_А реагента А:

ω =кС_А (7)

Коэффициент пропорциональности к на­зывают константой скорости реакции. По-видимому, в формуле (7) есть все, что нужно для расчета скорости. Но эта видимость обманчива. Концентрация С_А, определяющая скорость,— это концент­рация у самой поверхности. Обозначим ее с_п. Мы не имеем возможности не­посредственно измерить эту концентра­цию: слишком тонок этот приповерхност­ный слой, толщина которого порядка раз­мера молекулы. Измерить мы можем лишь концентрацию вещества А в ядре потока с_я; но она не равна с_п, и задача состоит в том, чтобы их связать.

Рассмотрим реше­ние этой задачи так. В урав­нениях (7) и (4). Что такое ω? По опре­делению, скорость гетерогенной реак­ции — это количество вещества, реаги­рующее в единицу времени на единице поверхности. А поток g_т — количество вещества, подводимое в единицу времени к единице поверхности. Но если реакция подходит стационарно (а это главный случай, наиболее важный для анализа), то

ω = g_т (8)

Действительно, если ω>g_т, то откуда берется то вещество, которое реагирует, но не подводится к поверхности? А если ω<g_т , то куда девается избыток подво­димого вещества?

Но из соотношения (8) следует ра­венство правых частей формул (7) и (4), т. е. кс_п=β(с_я—с_п), откуда с_п= βс_я/(к+ β). Подставляя это выражение в урав­нение (7), получим:

(9)

Уравнение (9) почти полностью аналогично уравнению (7). Только вместо неизвестной с_п здесь известная величи­на с_я, а вместо коэффициента к, отра­жающего химизм реакции, величина к', которая учитывает как скорость реак­ции, так и перенос вещества. Легко также получить следующее соотношение: к′= кβ/(к+β) или

к′=1/β+1/к. (10)

Формулу (10) можно понимать так. Левая часть — общее сопротивление пе­реносу, которое складывается из диффу­зионного сопротивления 1/β и кинетиче­ского сопротивления 1/к. Если β>>к (быстрая диффузия, медленная реак­ция), то из (10) следует: k'≈k ω≈kС_я. В этом случае лимитирует кине­тика (медленная химическая стадия); го­ворят, что реакция проходит в кинети­ческой области. Наоборот, если β<<к (реакция много быстрее диффузии), то к′≈ β и ω≈ β С_я , т. е. лимитирует диф­фузия; реакция проходит в диффузион­ной области. Наконец, если к ≈ β , то ли­митирующей стадии нет, реакция про­ходит в промежуточной области.

Что это значит практически? Для этого нужно учесть, что сильнее всего влияет на к и на β. Величина к наибо­лее сильно зависит от температуры. С по­вышением температуры на 10° обычно наблюдается рост к в 2—3 раза. В то же время к не зависит от состояния по­тока: турбулентный он или ламинарный, быстрый или медленный, все это на хи­мизм реакции не влияет.

Наоборот, β сильно зависит от ско­рости потока (чем сильнее выражена турбулентность, тем тоньше пограничный слой) и довольно слабо зависит от тем­пературы. Если движущаяся фаза — газ (так бывает чаще всего), то зависимость (β от температуры почти совсем отсут­ствует. Поэтому кинетическая область наибо­лее характерна для низких температур, а диффузионная — для высоких. Повы­шение скорости газа способствует переходу в кинетическую область. Подроб­ный анализ уравнения (10) показывает, что зависимость ω от температуры Т имеет характер, изображенный на рис. 5. В нижнем левом углу — кинетическая область. При низких температурах ско­рость реакции мала, но зато быстро ра­стет с ростом температуры. При высоких температурах рост скорости существенно замедляется. Теперь константа скорости реакций велика и продолжает расти, но мы этого не замечаем: лимитирует уже диффузия, которая с ростом температуры почти не ускоряется.

Если мы хотим ускорить процесс, про­ходящий в кинетической области, нужно прежде всего повысить температуру; если же область диффузионная, то нуж­но думать о турбулизации потока, по­вышении его скорости. Примером может служить процесс окисления древесины. Это очень слож­ный процесс и в действительности не полностью гетерогенный (горение идет не только на поверхности, но и в газовой фазе, куда выделяются продукты сухой перегонки). Но в основном реакция идет все же на поверхности. Этот процесс может проходить в двух основных ва­риантах. Первый — медленное окисле­ние при сравнительно низких температу­рах под действием микроорганизмов — гниение. Оно проходит в кинетической области. Второй — быстрый, высокотем­пературный — горение, проходящее в диффузионной области..

Проверим, как выведенные нами зако­номерности соблюдаются в этом случае. Скорость гниения (при достаточной влажности) зависит в первую очередь от температуры: бревно, которое на Зем­ле Франца-Иосифа пролежит почти це­лым десятки лет, в джунглях Лаоса сгниет за год. В то же время гние­ние происходит почти с одинаковой ско­ростью и в штиль, и в шторм. А вот с горением — дело совсем иное. Известно,- что часто, чтобы заста­вить дрова разгореться, на них дуют. Задумывались ли вы, что это значит с точки зрения химии? Дуем мы возду­хом из легких, содержащим не 21 % кислорода, а всего около 16 %. Скорость реакции должна бы уменьшиться! Кроме того, дуя, мы подводим в зону реакции холодный воздух: температура сни­жается, константа скорости реакции уменьшается. А дрова, казалось бы, во­преки химии, разгораются. Почему? Да потому, то когда мы дуем, мы утончаем пограничный слой и облегчаем диффу­зию кислорода. Для реакции, идущей в диффузионной области, это оказы­вается главным.

Рис. 4. Зависимость скорости реакции от температуры

ПРОДОЛЬНОЕ СМЕШЕНИЕ И РАСПРЕДЕЛЕНИЕ ВРЕМЕНИ ПРЕБЫВАНИЯ

Теперь перейдем к рассмотрению дру­гого направления смешения — продоль­ного, обусловленного целым рядом об­стоятельств. В разных точках попереч­ного сечения аппарата скорости могут быть разными: либо из-за влияния сте­нок, как в ламинарном потоке, либо, например, из-за неравномерно распреде­ленных загрязнений. Продольное смеше­ние характерно и для турбулентного по­тока, где пульсации скорости приводят к взаимному перемешиванию впереди идущих и последующих частиц. Правда, обычно относительная интенсивность пе­ремешивания в турбулентном потоке меньше, чем в ламинарном, так как ска­зывается выравнивание скоростей по се­чению, о котором мы говорили при опи­сании турбулентного потока.

Наконец, сильнейшее продольное пе­ремешивание возникает, когда в аппара­те происходят процессы, связанные с мощными циркуляционными потоками. Так бывает, если в аппарате вращает­ся мешалка. Тот же самый эффект про­изводит барботаж — пробулькивание пу­зырей газа через жидкость, а также не­которые другие процессы взаимного дви­жения двух фаз (жидкости в жидкости; газа или жидкости, которые проходят через слой твердых частиц, перемеши­вая их).

Важное следствие продольного сме­шения — неравномерность времени пре­бывания. Если две частицы вошли в аппарат одна за другой, а затем вто­рая нагнала первую, перемешалась с ней и вышли они из аппарата вместе, то это значит, что первая частица пробыла в аппарате большее время, чем вторая. В результате каждая частица имеет свое, отличное от большинства других время пребывания.

В таком случае поток можно охарак­теризовать двояко. Одна характеристика описывает различия во времени пребы­вания разных частиц. Это довольно сложная характеристика, и о ней мы поговорим позже. Другая — усреднен­ная характеристика потока: среднее вре­мя пребывания. Среднее время τ легко найти, поскольку оно равно отношению объема аппарата V_р (или, точнее, той его части, через которую движется по­ток) к расходу жидкости V_с (т. е. объему жидкости, протекающему через аппарат в единицу времени):

τ= V_р / V_с . (11)

Величина τ характеризует поведение ча­стиц в среднем. Как почти всякая усред­ненная характеристика, она, с одной сто­роны, очень проста, но, с другой — хо­рошо известно, что часто такие харак­теристики недостаточны.

Тем не менее, в каждом конкретном случае нужен анализ. Есть ведь и такие задачи, когда важно именно среднее. Если мы будем рассчитывать, какая мас­са сыпучего материала поместится в ва­гоне объемом 50 м³, для нас важна имен­но средняя плотность материала, а то, как эта плотность варьирует от точки к точке, менее существенно. Так, может быть, в случае потока такое же поло­жение? Одни частицы будут проходить через аппарат за время, меньшее чем τ, и в них реакция пройдет недоста­точно полно. Но зато другие частицы задержатся в аппарате (такие найдутся обязательно, так как среднее должно быть равно τ, а для этого нужны сла­гаемые и меньшие, и большие величи­ны τ). В этих частицах реакция пройдет полнее, чем за среднее время. На вы­ходе те и другие частицы перемешают­ся, и степень превращения исходных ве­ществ усреднится. Не окажется ли так, что эта средняя степень превращения такая же, как если бы все частицы реаги­ровали одинаковое время τ

Оказывается, в подавляющем боль­шинстве случаев степень превращения зависит не только от τ, но и от того, из каких конкретных значений времени пребывания складывается это среднее. Это обусловлено следующей особен­ностью большинства химических реак­ций: по мере протекания реакции ее ско­рость падает, так как остается все мень­ше и меньше исходного вещества. В ре­зультате степень превращения окажется тем выше, чем равномернее время пре­бывания, чем ближе к среднему конкрет­ные его значения для разных частиц.

Эту закономерность можно проил­люстрировать следующим примером. Представим себе цех, в котором рабо­тают 100 рабочих. Режим работы: 8 ча­сов в день в одну смену. Однажды ра­бочие решили, что им удобнее работать иначе: половина будет работать не 8, а 4 часа, и у них освободится боль­шая часть дня для личных дел. Но зато другая половина будет работать 12 ча­сов — 8 за себя и 4 за тех, кто ушел раньше. Потом они станут менять­ся, так что все будет справедливо.

Есть и другая сторона вопроса: ра­бота по 12 часов вредна для здоровья. Но мы обсуждать это не станем, а по­пытаемся лишь оценить вот что: если цех начнет работать по новому режиму, возрастет или нет производительность труда? Легко понять, что производитель­ность уменьшится. Действительно, 50 ра­бочих будут уходить с работы через 4 ча­са не уставшие, полные сил, а 50 других будут за них работать, но работать после 8-часового рабочего дня, когда они уже устали и их работоспособность упала.

Точно то же происходит, если в по­токе, в котором проходит реакция, вре­мя пребывания разных частиц неодина­ково. С теми частицами, которые имеют малое время пребывания, из аппарата выходит много непрореагировавшего вещества. В частицах, которые находи­лись в зоне реакции больше среднего времени, степень превращения велика; но выигрыш из-за большого времени пребы­вания меньше, чем проигрыш из-за не­достаточного времени, поскольку ско­рость реакции уже упала и за это избы­точное время реагирует мало вещества.

В идеальном вытеснении равномерно распределены скорости и соответственно время пребывания. Поток движется не как жидкость, а как твердый поршень, вдвигаемый в аппарат: все частицы вме­сте. Иногда его так и называют — порш­невой поток. Но равномерности распре­деления концентраций в этом потоке нет. Например, если некоторое вещество А превращается в вещество R, то у входа будет много А и мало В, а затем кон­центрация А станет убывать, а R — возрастать.

В идеальном смешении, наоборот, равномерно распределены концентрации. В нем и поперечное, и продольное сме­шение полное. А как скорости частиц и время пребывания? О скоростях здесь говорить трудно, поскольку вряд ли мож­но представить себе идеально переме­шиваемую жидкость. Во всяком случае ясно, что хорошее смешение возможно лишь при очень сложной картине пото­ка: с многократной циркуляцией, с раз­витой турбулентностью. Что же касается времени пребывания, то оно разное у разных частиц.

И если для идеального вытеснения формула (11) определяет время пребы­вания любой из частиц, то для идеаль­ного смешения — это лишь среднее вре­мя пребывания; та или иная конкрет­ная частица может находиться в аппа­рате совсем иное время.

В идеальном вытеснении частицы дви­жутся, как солдаты на параде: каждый равняется на всех, никто не обгоняет и не отстает, и если один прошел пло­щадь за какое-то время, то и любой другой затратит на этот путь то же самое время. Идеальное смещение подобно на­родному гулянию на той же площади: каждый описывает замысловатую траек­торию; кто-то может войти на площадь и тут же уйти, а кто-то будет бродить по ней часами.

Встречаются ли на практике потоки, достаточно близкие к нашим схемам? Да, и довольно часто. Наиболее близок к идеальному вытеснению поток в аппа­ратах типа труб (или колонн). Правда, если поток ламинарен, то параболиче­ский профиль скоростей не позволяет рассматривать его как близкий к идеаль­ному. Но при росте турбулентности ско­рости выравниваются, и часто такой по ток мы можем считать «почти идеаль­ным». Особенно же близок к идеальному поток, если аппарат заполнен какими-либо неподвижными твердыми частица­ми, между которыми проходит (фильт­руется) жидкость. Это довольно часто встречающийся случай: частицы могут быть, например, гранулами катализатора или насадкой (телами, по которым рас­текается жидкость, чтобы увеличилась поверхность ее взаимодействия с газом). Слой частиц сильно выравнивает поток жидкости, и вытеснение в таком потоке очень близко к идеальному.

Аппараты, в которых поток близок к идеальному смешению, пожалуй, еще более разнообразны. Прежде всего, это резервуары с мешалками, через которые проходит поток жидкости. Но интенсивно перемешивать жидкость может не только мешалка. Один из лучших способов перемешива­ния — барботаж. В то же время барботаж создает большую поверхность, на которой газ (или пар) может взаимо­действовать с жидкостью, так что барботажные аппараты весьма широко рас­пространены в химической технологии. Движение жидкости через барботажный слой — часто почти идеальное смеше­ние; газ движется по-иному, и описа­ние потока для него будет другим. Да­лее, очень важный случай, когда осу­ществляется интенсивное перемешивание во всех направлениях,— это псевдоожи­жение. Оно возникает тогда, когда сквозь слой твердых частиц снизу подается по­ток газа (реже — жидкости). При этом в определенном диапазоне скоростей ча­стицы приходят в такое движение, когда они и не неподвижны, и не уносятся потоком, а циркулируют в объеме слоя, который напоминает по виду кипящую жидкость; такой слой называют псевдо-ожиженным или кипящим. Опять же дви­жение газа в этом слое далеко от идеаль­ного смешения (и от идеального вытес­нения часто тоже); но движение твердых частиц — практически идеальное сме­шение.

Зададимся вопросом: как различия между идеальными потоками сказывают­ся на протекающих в них химических реакциях? По сути дела, это вопрос и о том, стоит ли заниматься продольным перемешиванием. Если разница между идеальным вытеснением и идеальным смешением невелика, то скорее всего остальные случаи тоже не так уж сильно отличаются, и заниматься этим не очень интересно. Иное дело, если разница ве­лика. Тогда нужно внимательно анали­зировать реальные потоки, выяснять, на­сколько они близки к идеальным, и, по-видимому, разрабатывать способы опи­сания не только идеальных, но и реаль­ных потоков.

Сопоставление идеальных потоков начнем с качественного анализа. Пусть мы проводим некоторую реакцию А—> R. Естественно, наша цель — провести реак­цию как можно полнее. Полнота про­ведения реакции характеризуется сте­пенью превращения Х:

(12)

Здесь G_A,0 и G_A,K -— количество вещест­ва А в исходной жидкости и в жидко­сти после реакции. Где будет выше X — в аппарате вытеснения или смешения, если среднее время пребывания оди­наково?

Начнем наш анализ с обсуждения влияния равномерности (или неравно­мерности) распределения времени пребы­вания. Такой анализ мы уже провели (разбирая режимы работы 100 рабочих в цехе), пришли к выводу, что равно­мерное распределение времени благо­приятствует полноте протекания реак­ции, а следовательно, в аппарате идеаль­ного смешения степень превращения должна оказаться выше.

Попробуем подойти к этому вопросу с другой стороны. Выясним, как влияет на ход реакции выравнивание концен­траций, характеризующее поток идеаль­ного смешения. При этом сначала об­ратим внимание на следующее. Мы гово­рили, что в идеальном смешении кон­центрация любого вещества одна и та же во всех точках внутри аппарата. А что делается на входе потока и на его вы­ходе? Для нашего анализа очень важно понять, что на выходе концентрации всех веществ — такие же, как в объеме, т. е. состав жидкости на выходе и внут­ри аппарата один и тот же. А вот на входе концентрации (и температура) претерпевают скачок, поскольку входя­щая жидкость мгновенно смешивается с содержимым аппарата.

Изобразим графически изменение концентрации реагента А по длине ап­парата (рис. 6). Пусть начальная кон­центрация С_А,0 и конечная С_А,К заданы. На оси абсцисс отложены значения про­дольной кординаты /, причем l=0 в на­чале аппарата, l=L в его конце. Часть графика левее l=0 соответствует трубе, вводящей смесь в аппарат; правее l=L — трубе, отводящей прореагировав­шую смесь.

Рис. 5. Распределение концентрации по длине реактора: 1 - аппарат идеального вытеснения; 2- аппарат смешения.

Для случая потока идеального вытес­нения изменение концентрации по длине можно изобразить кривой 1: жидкость движется по аппарату, идет реакция, C_А уменьшается. В потоке идеального смешения (ломаная 2) концентрация па­дает от C_А,0 до C_А,K сразу, скачком, у входа. И дальше до выхода она неизменна.

Теперь сравним значения C_А в ка­ких-то поперечных сечениях обоих аппа­ратов. Какое бы сечение (кроме самого конца) мы ни взяли, концентрация C_А в аппарате вытеснения окажется выше, чем в аппарате смешения. А скорость реакции почти всегда тем больше, чем выше C_А. Поэтому в любом сечении потока вытеснения скорость реакции будет выше, чем в соответствующем сечении потока смешения, и, следовательно, что­бы степень превращения в этих аппа­ратах была одинаковой, объем аппарата смешения должен быть больше, при рав­ных же объемах величина X в аппарате смешения окажется ниже.

Но все приведенные рассуждения еще недостаточны. Да, действительно, при равных объемах данная реакция полнее пройдет в аппарате вытеснения. Но на­сколько? Если разница невелика, то не окажутся ли более вескими иные соображения? Например, такое. Благодаря интенсивному перемешиванию в аппара­те смешения выше коэффициенты тепло- и массоотдачи, поэтому отвод тепла в таком аппарате может быть организован проще. Для более основательного сужде­ния одних качественных оценок мало. Нужны оценки количественные, для чего необходимо привлечь математическое списание протекания реакции в том и другом потоке.

Как и при анализе реакции на поверх­ности катализатора, будем считать, что скорость реакции превращения А в В пропорциональна концентрации реаген­та А:

(13)

Отличие от формулы (7) незаметно. Но оно есть. Скорость реакции, прохо­дящей на поверхности катализатора, оп­ределяется как количество реагента, пре­вращающееся в единицу времени на еди­нице поверхности. Здесь же реакция идет в объеме, и величина ω в уравне­нии (13) относится не к единице по­верхности, а к единице объема. Заме­тим, что такую реакцию, скорость кото­рой пропорциональна концентрации ре­агента в 1-й степени, называют реак­цией первого порядка. Это во многих отношениях простейший тип реакций; но основные выводы, которые получаются при ее анализе, можно распространить на весьма широкий круг реакций.

Итак, реакция со скоростью, описы­ваемой формулой (13), проходит в по­ токе. В потоке идеального вытеснения протекающая реакция будет приводить к уменьшению концентрации вещества А (и, следовательно, росту концентрации R), как это показано на рис. 6. Изменение C_А -можно описать дифферен­циальным уравнением

(14)

Здесь в левой части — производная от концентрации; знак «минус» справа обу­словлен тем, что С_А убывает во времени. Решение уравнения (14) хорошо извест­но в математике:

(15)

Для конца аппарата получаем

(16)

где τ, находимое по формуле (11), в ап­парате идеального вытеснения — время пребывания частиц протекающей жидко­сти. График уравнения (15) и есть верх­няя кривая на рис. 6.

Описание реакции в аппарате идеаль­ного смешения приходится строить со­всем по-иному. Для этого аппарата за­писать уравнение в виде формулы (14) нельзя, поскольку нет единого времени, определяющего изменение концентрации для любой частицы. Перемешивание ве­дет к тому, что если мы будем дви­гаться от входа к выходу, никакого из­менения С_А не происходит. Но зато ско­рость реакции во всех точках объема одинакова, а это позволяет очень про­сто записать для такого аппарата урав­нение материального баланса.

Материальный баланс — один из важнейших методов описания и анализа химико-технологических процессов. Он выражает закон сохранения вещества; уравнение баланса соответствует ут­верждению: приход вещества равен рас­ходу вещества. При описании химиче­ских реакций в потоке обычно записы­вают отдельное уравнение баланса для каждого из веществ.

Изобразим материальные потоки в нашем аппарате (рис. 7). В аппарат объема V_Р входит жидкость в количест­ве V_С (в единицах м³/с) и выходит та­кое же количество (изменение объема жидкости в процессе реакции мы для простоты рассматривать не будем; часто оно бывает пренебрежимо малым). На входе С_А=С_А,0, С_R=0; на выходе концент­рации С_А и С_R ^:— такие же, как в лю­бой точке объема аппарата. В аппарате проходит реакция А—>R, скорость кото­рой определяется уравнением (13).

Составим баланс за единицу време­ни для вещества А. Приход А — это то количество, которое внесет в аппа­рат входящий поток; он равен

V_С С_А,0. Рас­ход же состоит из двух слагаемых. Во-первых, та часть А, которая не успела прореагировать, уходит с потоком нару­жу; ее количество составляет V_С С_А. Во-вторых, А расходуется в реакции; этот расход равен произведению скорости реакции на объем аппарата V_Р или, с учетом формулы (13), V_РС_А. Так как приход равен расходу, то

V_С С_А,0 = V_С С_А + V_РС_А (17)

Рис. 7. Схема материальных потоков в аппарате смешения

Чтобы легче было сопоставлять урав­нения (16) и (17), поделим обе части последнего на V и учтем, что V_Р / V_С =τ , а С_А=С_А,К :, откуда

. (18)

Для сравнения обоих типов потока нетрудно сделать следующий расчет. Пусть нам нужно обеспечить в аппарате некоторую степень превращения %. Из уравнений (16) и (18) с учетом (11) легко вывести необходимый объем аппа­ратов вытеснения

Vвыт= V_С ln(1-X)/k (19)

и смешения Vcм=X Vc/[k(1-X)] (20)

А теперь проведем такое сопоставле­ние. Заданную степень превращения можно получить и в аппарате вытеснения объемом Vвыт, и в аппарате сме­шения объемом Vсм Естественно, что при разных значениях Х объемы и их соот­ношение будут неодинаковыми. Посмот­рим, как меняется отношение Vсм/ Vвыт для различных Х:

X	0,5	0,7	0,9	0,95	0,99	0,999
Vсм/ Vвыт	1,5	2	4	6	22	140

Вот теперь можно сделать более обос­нованные выводы. Уже из наших качест­венных рассуждений следует, что требуе­мый объем аппарата вытеснения будет меньше. Но во сколько раз меньше — это зависит от того, какой степени пре­вращения нужно добиться. Если требуе­мая степень невысока, то различие в объемах идеальных потоков хотя и ощу­тимо, но не столь велико, чтобы цели­ком и полностью определять выбор типа аппарата. Может даже оказаться, что более выгодным будет аппарат, впятеро больший по объему, но зато устроен­ный проще и позволяющий легче отво­дить тепло реакции. Однако если тре­буется степень превращения порядка 0,99 и выше, то объем аппарата смешения становится нереально большим, особенно при возрастании количества перерабаты­ваемой жидкости (множитель V в урав­нении (20). Поэтому вопросы продоль­ного перемешивания стали особенно важ­ными на современном этапе развития хи­мической технологии.

Нынеш­нее химическое производство разительно отличается от прежнего. Важнейшими объектами современной химической тех­нологии стали агрегаты большой еди­ничной мощности, каждый из которых выпускает продукции больше, чем хим­комбинат 50-х годов. Эти агрегаты не могли бы работать, если бы при их про­ектировании самым тщательным образом не прорабатывались все особенности движения потоков в аппарате.

Необходимо отметить еще следующее обстоятельство. Степень превращения исходных реагентов — не единственная характеристика реакции, интересующая технолога. Не менее важно, во что пре­вратятся реагенты. Очень часто наряду с той реакцией, которая нам нужна (це­левая), идут и другие, побочные процес­сы, сопровождающиеся образованием лишних, а то и просто вредных продук­тов. Для того чтобы определить, в какой мере реакция прошла в нужном нам направлении, рассчитывается еще одна (кроме степени превращения) важная характеристика — селективность. Не вдаваясь в математические детали рас­чета, отметим лишь, что селективность определяет, сколько получилось целе­вого продукта по отношению к сумме всех получившихся. Селективность также может сильно зависеть от степени про­дольного перемешивания, но эта зависи­мость окажется неодинаковой для раз­ных типов реакций.

Рис. 8. Изменение концентрации вещества во времени

Вот случай последовательной побоч­ной реакции: исходный реагент превра­щается в целевой продукт, но тот, в свою очередь, может вступать в реакцию, да­вая уже побочные продукты. Например, мы хотим получить хлористый метил СН₃С1 при реакции метана с хлором. Но образующийся хлористый метил так­же может хлорироваться, давая СН₂С1₂, который в данном случае не нужен.

Пусть реакция протекает по схеме: А→ R → S где R — целевое вещество. Концентрации веществ во времени будут изменяться так, как показано на рис. 8. Исходное вещество все время расходует­ся; для продукта R сначала превали­рует накопление, но потом вещества R становится все меньше, и под конец оно целиком перейдет в S. Если проводить этот процесс в аппарате вытеснения, можно подобрать время реакции таким образом, чтобы концентрация R ока­залась максимальной, либо даже взять еще меньшее время пребывания, и хо­тя концентрация R в этом случае будет ниже максимальной, зато кон­центрация S снизится еще сильнее, т. е. селективность возрастет. А непрореагировавшее вещество А можно отде­лить от реакционной смеси и вернуть в начало процесса. Этот прием — цирку­ляцию реагента — применяют почти всег­да, если почему-либо не получается вы­сокая степень превращения.

Если ту же реакцию проводить в ап­парате смешения, то мы столкнемся со следующим обстоятельством. В этом по­токе, как уже говорилось, присутствуют частицы с малым временем пребывания. В них окажется сниженной степень пре­вращения, но зато высокой — селек­тивность. Но есть и такие частицы, время пребывания которых велико, значительно больше среднего. Вот в этих частицах образуется столько побочного продукта, что он загрязнит всю смесь и понизит селективность по сравнению с аппаратом вытеснения. Это подтверждается как рас­четами, так и богатым эксперименталь­ным материалом. К сожалению, и про­мышленные установки неоднократно да­вали резко сниженную селективность из-за влияния продольного перемешивания.

Не будем подробно обсуждать другой тип побочных реакций — параллельный, когда из одного и того же реагента может получиться либо основной про­дукт, либо побочный (например, при хло­рировании этилена может образоваться и хлорвинил СН₂=СНС1 и дихлорэтан

СН₂С1—СН₂С1). Здесь в зависимости от особенностей целевой и побочной реак­ции селективность может оказаться выше и в аппарате вытеснения, и в аппарате смешения, и одинаковой в обоих типах потоков.

Теперь поговорим вот о чем. Для очень многих химических процессов по­ток вытеснения является теоретически наилучшим, поэтому довольно многие (в том числе и некоторые специалисты) де­лают заключение: следовательно, поток смешения—наихудший. Это ошибка, при­чем ошибка не только фактическая, но и логическая. Почему? Каждый из нас интуитивно не может не чувствовать, что живет в мире, раз­вивающемся в борьбе противоположно­стей. И тогда в своих рассуждениях, доверяясь обыденному сознанию (а не научным истинам), мы невольно опи­раемся на стихийную диалектику: там, где есть свет, есть и тьма; где есть меньше, есть и больше; если есть наи­лучшее, есть и наихудшее. Именно с этим связана и ошибка в оценке достоинств и не­достатков идеальных потоков.

Во-первых, в тех случаях, когда по­ток идеального вытеснения — теорети­чески лучший, теоретически худшего просто не существует. Могут быть по­токи значительно худшие, чем идеальное смешение. Особенно плохо, если в потоке существуют застойные зоны — такие об­ласти, где жидкость практически непо­движна и не участвует в общем дви­жении.

Во-вторых, как уже упоминалось, ап­параты смешения обладают рядом до­стоинств: в них обычно сравнительно про­сто организовать отвод тепла, выделяю­щегося в реакции, их конструкция мо­жет оказаться проще, чем для других типов потока.

В-третьих, есть случаи (хотя и не частые), когда степень превращения в потоке смешения оказывается выше, чем в потоке вытеснения равного объема. Это вариант реакций с самоускорением, т. е. таких, скорость, которых сначала мала, затем растет и лишь к концу реак­ции снова падает. Явление самоускоре­ния связано с тем, что в процессе реакции вырабатывается некая субстан­ция, ускоряющая реакцию. Для примера рассмотрим процесс ферментации:— совокупность химических реакций, про­ходящих под воздействием микроорга­низмов. Пусть мы ввели в аппарат пи­тательную среду, в которой будет про­исходить процесс, и небольшую пор­цию микроорганизмов (порция чаще все­го невелика хотя бы потому, что пре­параты микроорганизмов дороги). Если это аппарат вытеснения, то вначале про­цесс будет идти медленно: мало микро­бов. Но по мере его протекания микробы размножаются, их число увеличивается, и в результате реакции ускоряются. Мно­гие, вероятно, наблюдали подобное яв­ление при приготовлении дрожжевого те­ста. Вначале, после того как смешают муку с водой и дрожжами и поставят тесто в теплое место, брожение идет не очень быстро, и на вид с тестом ничего не происходит. Но потом дрожжевых грибков становится все больше, броже­ние ускоряется, и, если недоглядеть, тесто «убежит» из квашни.

Но при таком проведении процесса объем аппарата используется очень пло­хо. Действительно, во всей его началь­ной части реакция идет с малой ско­ростью, и поэтому аппарат придется де­лать очень большим, Другое дело — ап­парат смешения, где во всем объеме можно поддерживать такой состав смеси (включая содержание в ней микробов), который отвечает максимуму скорости процесса.

Мы уже говорили о том, что в ряде случаев в аппарате смешения может по­лучиться и более высокая селективность, и тогда он превосходит своих конкурен­тов по всем статьям. Однако такие слу­чаи достаточно редки. Типичная ситуа­ция такова: с точки зрения продольного перемешивания аппарат вытеснения лучше, но слабое продольное смешение сопровождается слабым поперечным пе­реносом. В результате затруднен тепло­обмен, усложняется конструкция. Мож­но ли найти решение, объединяющее до­стоинства обоих идеальных аппаратов?

КАСКАД РЕАКТОРОВ СМЕШЕНИЯ

Что произойдет, если мы вместо од­ного большого аппарата смешения про­пустим реагирующий поток последовательно через несколько меньших по объ­ему, каждый из которых — тоже аппа­рат идеального смешения? Как будет вести себя такой каскад реакторов?

Вначале проведем качественный ана­лиз. Распределение времени пребывания в каскаде должно отличаться от рас­пределения в одном аппарате смешения. Действительно, рассмотрим какую-то ча­стицу, которая в первом аппарате каска­да пробыла очень мало времени, сразу попав на выход. Но вряд ли и во вто­ром аппарате она попадет в число са­мых быстроуходящих. А уж такое совпа­дение, чтобы эта частица уходила в числе первых из каждой ступени каскада, со­всем маловероятно. Таким образом, при прохождении ка­скада время пребывания отдельных ча­стиц выравнивается, приближаясь к среднему. Здесь проявляется очень об­щая закономерность, известная в теории вероятностей как закон больших чисел: если некоторое сложное событие скла­дывается из ряда элементарных, то, чем больше этих элементарных событий, тем слабее характеристики суммарного собы­тия колеблются относительно своих сред­них значений, тем менее вероятны силь­ные отклонения от среднего. Все это озна­чает, что чем больше в каскаде сту­пеней, тем ближе поток (по распреде­лению времени пребывания частиц) к идеальному вытеснению.

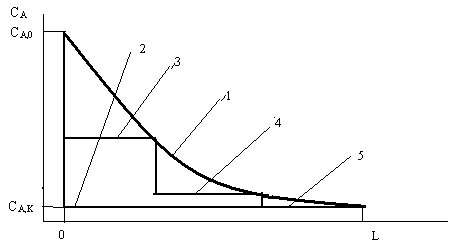
Рис. 9. Распределение концентрации реагента по длине реактора:

Теперь посмотрим, как замена одного аппарата смешения каскадом повлияет на распределение концентрации реаги­рующего вещества по длине (если считать весь каскад одним аппаратом).

Рис. 9 изображает изменение по длине аппарата концентрации реагента А, кото­рый расходуется в реакции А → R. Кри­вая / относится к аппарату вытесне­ния, горизонталь 2 — к -аппарату сме­шения; ход изменения концентраций в каскаде из трех аппаратов смешения ха­рактеризует ступенчатая линия, где циф­рой 3 обозначена первая ступень каска­да, 4 — вторая, 5 — третья. Для по­следней ступени концентрация А такая же, как в едином аппарате смешения. Но для всех предыдущих ступеней она больше, здесь соответственно выше и ско­рость реакции. С ростом числа ступе­ней каскада ломаная линия на рис. 9 будет приближаться к кривой /, и если ступеней достаточно много, то общий характер распределения концентраций приближается к идеальному вытес­нению.

Несложно получить и количественные оценки. Для этого рассматривают про­текание реакции сначала в первом ап­парате каскада; затем переходят ко вто­рому, учитывая при этом, что на входе во второй аппарат концентрации ве­ществ такие же, как на выходе из пер­вого; далее переходят к третьему и т. д. Для реакции первого порядка , длякоторой применительно к идеальным по­токам ранее получены уравнения (15) — (20), расчет для каскада аппаратов сме­шения приводит к следующей формуле:

, (21)

где -среднее время пребывания жидкости во всем каскаде (следователь­но, /п — среднее время пребывания в одной ступени); п — число ступеней. Естественно, при п=1 формула (21) сов­падает с (18); при п → ∞ формула (21) преобразуется в уравнение (16).

Для численного сопоставления нужно задаться определенным значением вели­чины к. Чем больше это произведение, тем больше объем аппарата либо быст­рее идет реакция. Сравним получаемые степени превращения при к=6: при п=1 Х=0,857 (один большой аппа­рат идеального смешения); при п =2 Х=0,938; при п =3 Х=0,963; при п=6 Х=0,984; при - п → ∞ Х=0,996 (аппарат идеального вытеснения).

Уже разделение единого потока сме­шения на две последовательные ступени позволяет резко повысить Х. Учтем, что при Х>0,9 каждая «дополнительная со­тая» — это уже немало. Для того чтобы получить в одном аппарате смешения значение х=0,938, его объем пришлось бы увеличить в 2,5 раза. Еще больший эффект дает дальнейший рост числа сту­пеней: для получения Х=0,963 объем ап­парата смешения должен увеличиться более чем в 4 раза, а для Х=0,984 — в 10 с лишним раз.

Поэтому в химической технологии ши­роко используется секционирование: ап­парат делят на секции поперечными пе­регородками с отверстиями. Эти отвер­стия служат для перетекания жидкости из одной секции в другую, причем цир­куляционные потоки, перемещающие жидкость навстречу основному потоку, на таких перегородках задерживаются. Поэтому продольное перемешивание происходит в основном только в преде­лах каждой ступени. Естественно, тот же эффект даст установка — на месте од­ного большого аппарата с мешалкой — нескольких маленьких, соединенных по­следовательно.

Секционирование влияет не только на степень превращения, но и на селек­тивность. Зачастую простейшее кон­структивное изменение — установка внутри аппарата нескольких перегородок с отверстиями — приводит к резкому улучшению всех основных показателей химического процесса.

ИЗУЧЕНИЕ РАСПРЕДЕЛЕНИЯ ВРЕМЕНИ ПРЕБЫВАНИЯ

Особенности структуры потока, свя­занные с продольным перемешиванием, одновременно связаны с неравномер­ностью времени пребывания. Поэтому один из лучших способов определить, какова структура данного потока,— это исследовать в нем распределение вре­мени пребывания.

Задача заключается в следующем. Через аппарат движется поток. В ка­кой-то момент мы отбираем на выходе пробу жидкости. И теперь хотим узнать, какая доля жидкости в этой пробе во­шла в аппарат секунду назад, какая — две, три, четыре и т. д. Но как это сделать? Ведь разные частицы пробы для нас неразличимы. Давайте сделаем их различными. Для этого выделим сре­ди всех частиц потока те, которые во­шли в аппарат в какой-то определен­ный момент. С этой целью мы их по­метим. Обычно это делается так. В опре­деленный момент (в дальнейшем будем принимать его за начало отсчета вре­мени, τ=0) в жидкость на входе ко­ротким импульсом добавляется малое ко­личество добавки-индикатора (ее назы­вают также «трассер»). Теперь, если на выходе появится меченая частица, нам будет точно известно, когда она вошла в аппарат и, следовательно, сколько вре­мени она в нем пробыла. Нам доста­точно получить лишь зависимость кон­центрации индикатора на выходе из ап­парата от времени (с_и от τ), поскольку она в определенном смысле представ­ляет собой портрет распределения време­ни пребывания.

Что можно использовать в качестве индикатора? Эта примесь должна обла­дать следующими свойствами. Во-пер­вых, она не должна влиять на движе­ние потока. Отсюда прежде всего сле­дует, что индикатора нужно добавлять очень мало. Во-вторых, с индикатором внутри аппарата ничего не должно про­исходить: он не должен вступать в реак­цию, оседать на стенках и внутренних деталях аппарата. Единственное его на­значение — двигаться вместе с мече­ными частицами. Наконец, в-третьих, он должен быть легко идентифицирован на выходе.

Если движущаяся в аппарате фаза — вода, то индикатором может быть рас­твор красителя (на выходе мы поста­вим колориметр) или раствор электро­лита (на выходе — измеритель элект­ропроводности, кондуктометр). Если дви­жется воздух, то в качестве примеси ча­ще всего используют газ, сильно отли­чающийся по теплопроводности: гелий (теплопроводность велика) или СО₂ (теплопроводность мала). На выходе — датчик теплопроводности.

Теперь подробнее исследуем зависи­мость С_и от τ. Рассмотрение этого вопроса существенно упрощается, если привести С_и и τ к безразмерному (приведенному) виду. Операция приведения очень широ­ко распространена в физике, и сейчас мы немного отвлечемся, чтобы поговорить об этом.

Что значит измерить какую-то вели­чину? Это — сравнить ее с неким эта­лоном. Измерить длину — сравнить дли­ну данного предмета с длиной платино­вой линейки, хранящейся в Севре (или, более современно, с длиной волны из­лучения, полученного в строго определен­ных условиях). Измерить массу — опять же сопоставить массу предмета с массой эталона килограмма и т. д. Каждый раз эталон — нечто совершенно чуждое данному конкретному измерению и зато об­щее всем измерениям данной величины.

Но можно поступать и иначе. Пред­положим, мы захотим определить размеры конкретной человеческой фигуры. И в качестве единицы (эталона) примем не метр, не сантиметр и даже не фут, а рост этого человека. Тогда , например, получится: ширина плеч — 0,276; окружность гру­ди — 0,596; длина руки — 0,447 и т. д.

Если теперь попытаться по этим дан­ным восстановить фигуру, то ока­жется, что полученный набор чисел оди­наково хорошо подходит и к самому человеку, и к статуэтке высотой 20 см, и к статуе в два человеческих роста. Эти числа определяют не размер пред­мета, а только его пропорции. При таком способе измерения все подобные пред­меты неразличимы.

Хорошо это или плохо? С одной сто­роны, описание внешности оказа­лось явно неполным. Вы так и не поняли, какого он роста (скрывать не станем — 180 см). Лишь после указания роста этот набор чисел оказался связанным с эталоном, а значит, и с остальными предметами окружающего мира. Но зато получена характеристика, обладающая общностью: ею описывается не только конкретный человек, но и ряд возмож­ных его изображений в разных масшта­бах.

Эти соображения оказались особенно важными после того, как понятие подо­бия удалось распространить на все фи­зические величины и явления. Можно говорить о подобии движения в потоках, подобии протекания химических реак­ций и т. д. Около века назад оформи­лась теория подобия, анализирующая яв­ления с позиций их подобия. Одна из важнейших возможностей, даваемых этой теорией, как раз и заключается в обобщенном характере описаний — описав поведение одного объекта, мы получаем характеристику любого объек­та, подобного данному; достаточно толь­ко учесть его размер (масштаб). Если наш первый объект — модель какого-то практически важного оригинала, то тео­рия подобия определяет правило пере­носа полученных зависимостей с моде­ли на оригинал и, таким образом, является одной из основ моделирования.

Одна из особенностей теории подо­бия — использование безразмерных ве­личин, т. е. величин, не связанных с об­щими эталонами, о которых говорилось вначале (размерность, по сути дела,— это и есть соотнесение с эталоном). Про­стейший способ получения безразмерной величины уже рассмотрен нами: сопо­ставление результатов измерения с при­нятым за единицу внутренним эталоном (в рассмотренном примере это был рост), характеризующим данную конкретную задачу. (Есть и более сложные способы: так, использованное нами при описании турбулентного потока число Рейнольдса, по сути, представляет собой безразмер­ную скорость.)

Теперь вернемся к распределению времени пребывания. Чтобы выразить τ и С_и в безразмерном виде, выберем внут­ренние эталоны (единицы). В качестве единицы времени естественно принять среднее время пребывания =V_P/V_C Без­размерное время т для любого момен­та / будет равно

τ=τ/. (22)

Единица концентрации Со определяет­ся следующим образом. Обозначим ко­личество индикатора, введенное на вхо­де, g₀, тогда

(23)

Для безразмерной концентрации С ин­дикатора на выходе имеем C=C_и/С₀

Переход от переменных τ, С_И к безраз­мерным τ и С сразу же позволяет рас­пространять полученные результаты на группу подобных друг другу случаев. Особенно ясно это преимущество в отно­шении величины с„. Ведь с_и пропорцио­нально g_о, т. е. чем больше мы введем индикатора, тем большую концентрацию получим; но g_о — величина, не имеющая отношения к характеру потока, связан­ная со случайными обстоятельствами опыта. В то же время С не зависит от этих обстоятельств. Использование τ так­же удобно: установив условия подобия (в ряде случаев это удается сделать), мы получаем одинаковое описание и не­большой лабораторной модели с малым средним временем пребывания, и боль­шого промышленного аппарата, где вре­мя велико. Есть и другое преимущество безразмерных переменных, но о нем мы поговорим немного позже.

Рис. 10. Зависимость безразмерной концентрации от безразмерного времени

Итак, наш опыт с вводом индикатора дал зависимость С от τ. Типичный (хотя далеко не единственно возможный) гра­фик функции С(τ) показан на рис. 10. Вначале на выходе нет индикатора. За­тем появляются первые его порции — те, которые метят частицы с наимень­шим временем пребывания. Потом С ста­новится больше, проходит через макси­мум и начинает убывать: основная мас­са индикатора прошла, и выходит то, что задержалось в зонах циркуляции и за­стоя. Через достаточно большое время концентрация С практически падает до нуля, хотя теоретически не исключается и асимптотический характер приближения кривой зависимости к нулю.

Дальнейшее выяснение физического смысла функции С(τ) связано с одним из фундаментальных понятий современ­ной математики — случайной величиной, о которой заранее нельзя точно сказать, какое значение примет она при нашем измерении. Мы не знаем, сколько зерны­шек окажется в арбузе, который соби­раемся разрезать; не знаем, каким будет время пребывания какой-то одной части­цы из числа тех, которые в данный момент входят в аппарат. И число зерны­шек, и время — случайные величины.

Но чтобы наша величина в качестве случайной стала предметом научного рассмотрения, необходимо, чтобы экспе­римент по ее измерению можно было проводить многократно, и каждый раз эта величина должна оставаться случай­ной. Например, мы заранее не знаем, сколько гор окажется на Титане — спут­нике Сатурна. Но это не случайная вели­чина: один раз сосчитаем и будем знать навсегда.

Важнейшая характеристика случай­ной величины — вероятность. Строго определить, что это такое, очень сложно. Нас удов­летворит приблизительное описание, не претендующее на строгость. Вероят­ность показывает, как часто в изме­рениях будет получаться данное значе­ние величины. Но ведь величина — слу­чайная, и в разных сериях измерений частота ее появления окажется различ­ной (иначе мы заранее бы знали, когда что получится). Это верно; но если числе измерений будет становиться все больше и больше, то эта частота окажется во ближе и ближе к вероятности. Вероятность и есть в некотором (не вполне строгом) смысле тот предел, к которому стремится частота при увеличении числа измерений и вокруг которого она колеблется в различных сериях.

Вероятность Р любого значения случайной величины заключена в предела от 0 до 1. Если Р=0, то данное значение практически никогда не появится в измерениях. Если Р=1, то во всех измерениях наверняка будет получаться именно данное значение. Например, если мы станем подсчитывать количество певчих птиц в ближайшей роще, вероятность того, что их число составит 10⁹ равна 0 (наверняка в роще не поместится миллиард птиц). Вероятность, равна 1, характеризует величины неслучайные. Так, сейчас у Земли с вероятностью имеется один крупный естественный спутник. В некоторых простых ситуациях определить вероятность можно исходя и числа возможных равновероятных результатов измерений. Скажем, при бросании игральной кости (кубика) вероятность того, что выпадет 5, равна 1/6. Для шести возможных вариантов вероятность того, что выпадет хотя бы один из них, равна 1, а вероятность любого конкретного варианта в 6 раз меньше. Все примеры, рассмотренные в преды­дущем абзаце, относятся к одному клас­су случайных величин, так называемым дискретным. У этих величин их возмож­ные значения — не любые, а отделены друг от друга каким-то интервалом. Число птиц, спутников, число очков при бросании кости — обязательно целые числа. Не может быть у планеты, скажем, 2,3 спутника. Есть дискретные величины, где интервал и не целый. Например, суммарный спин систем электронов мо­жет принимать значения, отделенные друг от друга интервалами, кратными ½. Но в любом случае у дискретных величин эти интервалы есть.

Другой случай — непрерывные слу­чайные величины, к ним относятся мас­са, время, скорость и т. п. Здесь в неко­торой области может получиться любое значение. Время может составить 1 с, 2 с, но может и 1,08356 с, и какое угодно другое значение.

Для непрерывных случайных величин вероятности приходится задавать по-осо­бому. Дело вот в чем. Вероятность того, что непрерывная случайная величина примет какое-то точно заданное значе­ние, всегда равна 0. Как же так? Ведь какое-то значение обязательно получит­ся. Да, но это будет не то значение, которое мы заранее задали. Мы задали 1,5, а получилось 1,5000001. И даже если получили 1,5000000, никогда нельзя ру­чаться, что еще через 200 знаков не поя­вится какой-то, отличный от нуля. Беско­нечный диапазон возможных значений, как угодно близких к заданному, и при­водит к тому, что для заданного значе­ния получаем Р=0.

Но нельзя же сказать, что все значе­ния непрерывной случайной величины равновероятны. Вероятность того, что масса яблока, сорванного с дерева, ока­жется равной точно 200 г, равна 0. Веро­ятность того, что эта масса окажется рав­ной точно 200 кг, тоже равна 0. Но ясно, что это в каком-то смысле разные нули: яблоко в 200 г нас не удивит, яблоко в 200 кг совершенно невероятно.

Для того чтобы определить вероят­ность значения непрерывной случайной величины, это значение надо задать не точно, а с каким-то интервалом. Вероятность того, что масса яблока окажется в пределах от 200 до 200,1 г уже не равна нулю, хотя и мала (потому что мал интер­вал в 0,1 г).

Записывается этот способ определе­ния вероятности так:

P(x≤ X ≤x+dx)=f(x)dx 25

Смысл формулы (25) таков. Здесь X —. случайная величина; х — какое-то ее зна­чение; dx — бесконечно малое прираще­ние (дифференциал) значения х. Левая часть обозначает вероятность того, что величина х окажется в интервале от х до х+ dx. Теперь обратимся к правой части. Множитель их введен сюда пото­му, что чем больше интервал, тем ско­рее «попадет» в него величина. Функция f(x) отражает то обстоятельство, что раз­ные значения х не равновероятны (точ­нее, что вероятность попасть в интервал шириной dx зависит от того, где на оси х расположен этот интервал). Эта функ­ция называется плотностью вероятности случайной величины.

Так вот, функция С(τ), оказывается, представляет собой плотность вероят­ности времени пребывания. Если выра­зить время не в приведенных, а в раз­мерных единицах, то

(26)

где С(τ) — та же самая безразмерная концентрация индикатора (делать ее раз­мерной нет смысла).

Как же можно использовать получен­ную плотность вероятности, т. е. функцию С(τ) или f(τ)? Прежде всего для ряда случаев знание этой функции позволяет непосредственно рассчитать ход химиче­ской реакции. Так, протекание реакции первого порядка (см. формулы 13, 16, 18) в потоке, где распределение времени пре­бывания характеризуется плотностью ве­роятности f(τ), дает на выходе такое значение концентрации реагента:

(27)

Рассчитать этот интеграл не так уж сложно, для чего, например, можно по­строить график функции от τ=0 до того значения τ, при котором эта функция для нас неотличима от нуля. Площадь под графиком приближенно равна искомому интегралу. В практиче­ских целях обычно пользуются более быстрыми и точными методами числен­ного интегрирования. Формула (27) по­казывает, что в этом простом случае для расчета процесса достаточно знать урав­нение скорости реакции (13) и функцию f(τ), которую можно получить из опыта с пропусканием индикатора.

В более сложных случаях не всегда можно получить аналогичную формулу. Тогда использование непосредственно функции C(τ) или f(τ) может быть затруднительно. Проще поступать по-другому: рассчитать на основе этой функ­ции некоторые характеристики времени пребывания как случайной величины и дальше пользоваться для анализа этими характеристиками.

Чаще всего рассчитывают две основ­ные характеристики. Первая характери­зует среднее значение случайной вели­чины. Раз величина случайная, то и получаемые для нее значения оказыва­ются разными. Но какова она в сред­нем? Около какого среднего колеблются отдельные ее значения? Оказывается, в теории вероятностей можно определить несколько разных средних. Но чаще все­го пользуются характеристикой, которая еще с XVII в. носит название мате­матическое ожидание. Название сегодня мало о чем говорит. Когда-то оно означа­ло ожидаемый средний выигрыш в азарт­ной игре. Азартные игры, особенно кос­ти, оказались прекрасной моделью, на которой изучали свойства вероятностей первые исследователи в этой области. Сейчас интересы математиков перемести­лись на совсем иные вопросы, а термин остался. По существу, математическое ожидание — то же самое, что среднее арифметическое, только записанное так, чтобы можно было рассчитать его через вероятности. Поэтому в дальнейшем бу­дущем будем называть его просто сред­ним и обозначать чертой над усредняе­мой величиной.

Среднее значение безразмерного вре­мени пребывания определяется формулой

(28)

Но эта формула практического интереса не представляет. Дело в том, что, приво­дя время к безразмерному виду, мы при­няли среднее время за единицу. И если дальше все правильно, то формула (28.) должна тождественно приводить к ре­зультату =1. Гораздо интереснее фор­мула, которую можно вывести из (28), позволяющая рассчитать Г из результа­тов опыта с вводом индикатора

(29)

Можно возразить — величину гораздо быстрее и про­ще рассчитать по формуле (11). Зачем такие сложности?»

Формула (29) сложна, это верно. Но зато ее можно использовать тогда, когда неизвестен объем, занимаемый потоком. А затем при помощи формулы (11) опре­делить этот самый неизвестный объем.

Работать таким методом первыми на­чали, по-видимому, спелеологи. Во мно­гих местах (например, на Южном берегу Крыма) важную роль играют речки, вы­текающие из подземных озер, спрятан­ных в пещерах. Такое озеро служит при­родным водохранилищем, и его объем важно знать для прогноза поведения реки. Но далеко не всегда удается об­мерить озеро непосредственно. Тогда к пещере отправляется экспедиция. Экспе­диция делится на два отряда. Один оста­навливается наверху, в том месте, где река выбивается из-под земли. Замерив расход воды в реке, он ждет. Другой от­ряд спускается в пещеру. И в заранее обусловленное время (например, ровно в полночь) спелеологи выливают в устье той подземной речки, которая впадает в озеро, бутылку индикатора. Чаще всего используют флюоресцеин. Даже очень разбавленные его растворы ярко флюо­ресцируют — светятся красивым зеле­ным светом. Начиная с момента ввода индикатора, наземный отряд каждые полчаса (или час, или 10 минут в за­висимости от ожидаемых размеров озера и от расхода воды) отбирает пробы воды для анализа на индикатор. Нужно сказать, зрелище это очень красивое и немного жуткое:

вся вода в реке све­тится изумрудным сиянием. Говорят, жители глухих уголков Пиренеев, где та­кие опыты проводил знаменитый фран­цузский спелеолог Н. Кастере, никак не могли решить, кто же эти странные люди, заставляющие светиться реки: посланцы сил добрых или дьявольских.

В химической технологии и, близких к ней отраслях объем аппарата всегда известен. Поэтому здесь такая задача встает лишь тогда, когда поток зани­мает не весь объем. Так, часто через аппарат движутся два потока: сверху — жидкость, а снизу — газ или пар. При этом скорость газа велика, и его вре­мя пребывания мало. А вот жидкость находится в аппарате значительно доль­ше, и если обрабатываемые вещества способны разлагаться, то желательно сделать время пребывания минималь­ным. Поэтому стоит подобрать такой режим работы, когда объем, занимаемый стекающей жидкостью, невелик и в со­ответствии с уравнением (11) мало вре­мя пребывания. При отладке такого ре­жима эксперимент с вводом индикатора может сослужить неоценимую службу.

Другой пример, когда, наоборот, ма­лое значение I является грозным призна­ком — это случай образования козла в шахтных печах.. Название звучит не­сколько комично, но в самом явлении ве­селого мало. Козел в печи — это при­липший к стенке или к деталям конст­рукции материал, на который налипают еще и еще порции; постепенно образует­ся большой ком, давящий на стенку, перегораживающий путь материалу. Ес­ли вовремя не принять меры, козел может стать таким большим, что при­ведет, к аварии с весьма тяжелыми по­следствиями. В домне, например, козел может весить много тонн. Такая махина способна обрушить футеровку печи, что потребует остановки на капитальный ре­монт и причинит громадные убытки.

Самый простой способ обнаружить зарождающийся козел, основан на том, что он, перегораживая путь части дви­жущейся в печи шихты, образует застой­ную зону, а это ведет к уменьшению ра­бочего объема и соответственно .

Теперь еще об одной характеристике случайной величины, очень важной для анализа структуры потока. Это характе­ристика разброса относительно среднего. Если трехкилограммовый пакет с кар­тофелем содержит 30 клубней, то средняя масса клубня составит 100 г. Но для нас не все равно, будут ли все 30 клубней при­близительно по 100 г (скажем, колебать­ся от 80 до 120 г) или в пакете будут лежать два гигантских клубня по 1,2 кг, а остальные 28 клубней — мелочь примерно по 20 г. В первом случае все зна­чения массы близки к среднему, во вто­ром наблюдается сильный разброс во­круг него. Наиболее принятая в теории веро­ятностей мера разброса — дисперсия, представляющая собой среднее значение квадрата отклонения случайной величи­ны от ее математического ожидания (оказалось удобнее изучать квадраты от­клонений, чем сами отклонения). Если нам нужно оценить не квадрат, а само отклонение, то достаточно извлечь из дисперсии корень квадратный и получим среднее квадратичное отклонение.

Рис. 9.Плотность вероятности времени пребывания для идеальных потоков: 1 - вытеснение; 2 - смешение

Формула для расчета дисперсии без­размерного времени пребывания имеет вид

(30)

В подавляющем большинстве случа­ев, чем больше дисперсия, тем дальше поток от идеального вытеснения. Для того чтобы яснее представить себе это, рассмотрим плотности вероятности для тех типов потока, которые были рассмот­рены раньше.

Для идеальных потоков графики С(т) показаны на рис. 9. Для идеаль­ного вытеснения, строго говоря, график построить нельзя. Действительно, опи­шем поведение индикатора, движущегося с потоком в аппарате идеального вытес­нения. При этом нам придется учесть од­но свойство плотности вероятности (фи­зически достаточно очевидное), согласно которому всегда

(31)

Левая часть выражения (31) задает вероятность того, что время пребывания частицы в интервале от 0 до ∞ примет какое-то значение, что будет в любом слу­чае, поэтому соответствующая вероят­ность и равна единице.

Теперь рассмотрим движение индика­тора. Для любого τ <1 на выходе нет ин­дикатора: с_и=0, С=0. Все частицы, по­меченные индикатором, движутся вместе, и ни одна из них еще не появилась на выходе. То же верно и для любого т>1; все меченые частицы уже вышли. При τ= 1 все частицы выходят одно­временно. На графике должен быть скачок вверх-вниз (пик), причем ширина этого пика равна нулю. Но мы уже гово­рили, что интеграл равен площади под кривой. Уравнение (31) требует, чтобы эта площадь была равна 1; тогда высоту пика придется считать бесконечной. Очень странная получается функция: всюду, кроме одной точки, она равна нулю; а в этой точке — бесконечный пик с площадью, равной 1. До начала нашего века такое, пожалуй, и функцией бы не назвали. Потом эта функция остро понадобилась физикам, и один из вели­чайших физиков XX в. П. Дирак ее ввел и назвал дельта-функцией. То, что по­казано на рис. 11, лишь весьма отдален­ное подобие дельта-функции, которую точно изоб­разить невозможно.

Для идеального смешения функции С(т) совсем другая. Она описывается формулой

С=ехр[-τ] (32)

Тоже довольно необычная зависимость. В этом потоке наиболее вероятно, что время пребывания частицы окажется очень близким к нулю: не успеет она войти в аппарат, как идеальная мешалка перекинет ее к выходу, и частица покидает аппарат, не успев принять учас­тие в реакции (об этом мы уже гово­рили). Наряду с такими частицами есть и другие, хотя и в гораздо мень­шем количестве. Они долго странствуют по аппарату, перемешиваемые по всему объему, и теоретически на выходе могут найтись частицы, вошедшие в аппарат как угодно давно.

Дисперсия времени пребывания для потока идеального вытеснения равна нулю, здесь никакого разброса вокруг среднего нет. Для потока идеального смешения а²(т) = 1. Расчет легко провес­ти по формулам (30) и (32).

Для очень многих реальных потоков величина σ²(τ) лежит между 0 и 1. Их в первом приближении можно рассматри­вать как промежуточные случаи между обоими идеальными потоками. Но воз­можны иные случаи, и об этом мы уже говорили. Разумеется, исключен вариант, когда σ²(τ) <0, но больше единицы дис­персия может быть, и теоретически мо­жет встретиться сколь угодно большое значение σ²(τ). Правда, если σ²(τ) >1, то это означает, как правило, чрезвы­чайно плохую организацию потока; обыч­но так получается, когда в аппарате имеется очень большая застойная зона, а движущийся поток проходит малой частью объема и поэтому весьма быстро. Другой вариант, приводящий к большим значениям σ²(τ) , напоминает предыду­щий: это случай резкой неравномерности потока по поперечному сечению, когда нет настоящей застойной зоны, но в од­них частях сечения скорость в несколько раз больше, чем в других. К сожалению, этот вариант довольно часто встречается в аппаратах большого поперечного сече­ния, и создание агрегатов большой единичной мощности ставит перед иссле­дователями непростую задачу: добивать­ся равномерности потока в крупномер­ных аппаратах. Наконец, проследим поведение функ­ции С(τ) для каскада аппаратов смеше­ния

Рис. 10. Плотность вероятности времени пребывания для каскада аппаратов смешения

. Графики на рис. 10 построены с учетом того, что — среднее время пребывания во всем каскаде, рассмат­риваемом как один аппарат. Уже при п=2 график непохож на идеальное сме­шение (п=1):С=0 при τ=0, а затем кривая проходит через максимум. Чем больше п, тем круче и выше пик; как мы уже отмечали, предел n → ∞­ coответствует переходу к дельта-функции. Интересно выражение для дисперсии:

(33)

Довольно часто понятие каскада ис­пользуют в качестве схемы, с той или иной степенью приближения описываю­щей реальный поток, отличающийся от обоих идеальных типов. Тогда один аппарат каскада рассматривают как участок аппарата (ячейку). Такую схему называют ячеечной моделью потока. Экс­перимент с вводом индикатора позво­ляет по формуле (33) легко определить параметр модели — число ячеек, при ко­тором схема лучше всего соответствует нашему потоку.

Химические реакторы с неидеальной структурой потока.

При составлении математической модели реакторов идеального смешения и вытеснения был сделан ряд допущений, облегчающих как построение моделей, так и расчеты на их основе. Однако эти допущения не всегда близки к реальным условиям. Рассмотрим сначала основные причины отклонений от идеальности.

1. Причина отклонения в непрерывно действующих (проточных) реакторах можно охарактеризовать следующим образом: в аппарат поступает реакционная смесь и каким-то образом перемещается от входного отверстия до выходного

. При этом предполагается, что все элементы реакционного потока находятся в реакторе некоторое время, в течение которого может протекать химическая реакция. В общем случае время протекания отдельных элементов потока в проточном аппарате – это непрерывная случайная величина, значение которой может меняться от 0 до бесконечности. Может оказаться так, что какой-то элемент потока в реакции не участвует, так как он попадает в реакторе в так называемую застойную зону. Здесь реакционная смесь задерживается и скорость химической реакции если не равна 0, то существенно отличается от скорости реакции в основном потоке. Возможные варианты застойных зон:

2) Второй причиной, по которой часть реакционного потока может не применять участие в реакции, является наличие байпасов.

Образование внутренних байпасных линий

Особенно часто байпасы возникают при недостаточно продуманном конструктивном решении в аппарате, где реакционным пространством является поверхность зернистого катализатора.

Наилучшие результаты могли бы быть получены, если бы все элементы реакционного потока находились в зоне реакции строго одинаковое время. Это возможно в аппарате идеального вытеснения, характеризующимся плоским профилем линейных скоростей потока. Однако в реальных реакторах, даже близких к идеальному вытеснению, все-таки существует какое-то распределение элементов потока во времени пребывания, возможно вследствие частичного перемешивания элементов потока в осевом направлении. Такое перемешивание может возникнуть в результате молекулярной диффузии в двух соседних точках потока по длине реактора вытеснения концентрации участников реакции будут разными, разность концентрации ΔС является движущей силой диффузии. Наличие продольной диффузии приводит к нарушению поршневого течения потока – произойдет размывание поршня, если рассматривать некоторый элемент потока как поршень.

Наряду с молекулярной диффузией происходит турбулентная диффузия. Турбулентный поток отличается наличием направленных во все стороны хаотических пульсаций скорости относительно ее среднего значения. При этом пульсации в радиальном направлении приводят к выравниванию условий (концентраций, температуры) по поперечному значению и следовательно необходимы для реактора идеального вытеснения. Пульсации в продольном направлении, наоборот, приводят к тому, что одни элементы потока обгоняют основную массу, другие отстают от нее, т.е. происходит перемешивание или диффузия. Диффузия в осевом направлении происходит не только в турбулентном течении потока. Продольное перемешивание может быть следствием неравномерности поля скоростей, например при ламинарном течении жидкости. В этом случае элементы потока движутся в центре канала быстрее, чем у стенки. Если в какой-то момент времени τ поместить частицы, находящиеся в каком-то сечении потока, то в более поздние моменты τ₂, τ₃ помеченные частицы окажутся на поверхности параболоида, те из них, которые движутся по оси трубы, уйдут дальше всех, т.е. у самой стенки не сдвинутся с места – их скорость равна 0. И хотя характер движения не хаотический (в любой момент времени можно предсказать положение выбранной частицы), результат будет тот же, что и в случае молекулярной диффузии - размывание поршня. Такой вид диффузии носит название – тейлоровская диффузия.

τ₁ τ₂ τ₃ τ₄