Биофизика 02

нянь, що описують даний процес. У нашому випадку рівняння запишуться у вигляді:

Інактивація і виведення препарату

Рис. 2.14. Схема переміщення лікарського препарату в організмі.

де с1, с2, с3 — концентрація речовини в першому, другому і третьому блоці.

На наступному етапі побудови математичної моделі потрібно вирішити отримані рівняння, що не завжди можливо в загальному вигляді. У такому випадку їх вирішують за допомогою обчислювальної техніки.

Іноді число отриманих рівнянь можна скоротити. Всі процеси умовно розділяють на швидкі, середні та повільні. Припустимо, ми спостерігаємо за процесом протягом кількох годин. У такому випадку, процеси, які здійснюються протягом кількох хвилин, будуть швидкими, кілька годин — середніми, кілька діб — повільними. Тоді виходить, що, спостерігаючи за процесом кілька годин, ми не встигаємо простежити за повільними реакціями, і змінні, які входять до цих рівнянь, залишаються постійними протягом періоду спостереження. У той же час швидкі процеси встигають пройти на самому початку періоду спостереження і далі також залишаються постійними. Тому перемінні, що входять до складу рівнянь швидких процесів, можна замінити початковими значеннями, а перемінні, що входять до складу рівнянь повільних процесів — стаціонарними. Даний метод дозволяє скоротити число диференціальних рівнянь і число змінних. Наприклад, у вищенаведеній системі рівнянь концентрацію с2 можна вважати постійною.

При введенні якогось лікарського препарату часто потрібно знати часовий характер (кінетику) його розподілу в організмі. Якщо ліки було введено в недостатній дозі або вони дуже швидко розкладаються (або виводяться) з організму, то їх лікувального ефекту не буде досягнуто. З іншого боку, зайва доза може викликати небажані побічні ефекти. Модель, що буде розглянута нижче, дозволяє вибрати оптимальні дозу і періодичність введення препарату.

41

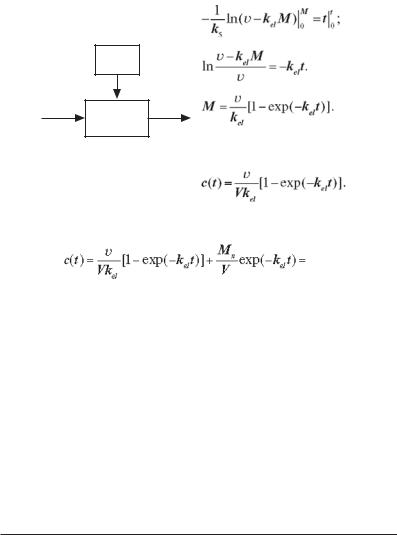
На практиці часто доводиться зустрічатися з проблемою підтримки постійної концентрації лікарського препарату в організмі. Для цього потрібно безупинно з постійною швидкістю уводити внутрішньовенно або внутрішньоартеріально препарат (рис. 2.15). При введенні (інфузії) препарату зі швидкістю v його кількість M у крові буде змінюватися відповідно до рівняння

dМ/dt = v – kelМ, де kel — константа швидкості виведення препарату з крові.

Проінтегруємо це рівняння в межах часу від 0 до t і кількості препарату від 0 до М:

Mn

Далі перейдемо від кількості препарату до його концентрації, для чого розділимо рівняння на уявний об’єм V:

(2.16) Як видно з рівняння (2.16), концентрація речовини з часом зростає й асимптотично наближається при t→∞ до постійного значення кон-

центрації

(рис. 2.16, крива 2). З (2.17) можна одержати значення швидкості, із якою варто вводити препарат для того, щоб його концентрація в крові дорівнювала необхідній (с*):

v = c*Vkel.

Для того, щоб якнайшвидше досягти бажаного ефекту потрібно в початковий момент часу ввести деяку дозу препарату (так звану навантажувальну, рис. 2.15), а після цього безупинно вводити препарат із

швидкістю v. Тоді в рівняння зміни концентрації в часі (2.16) додасться доданок, обумовлений навантажувальною дозою (Mn):

42

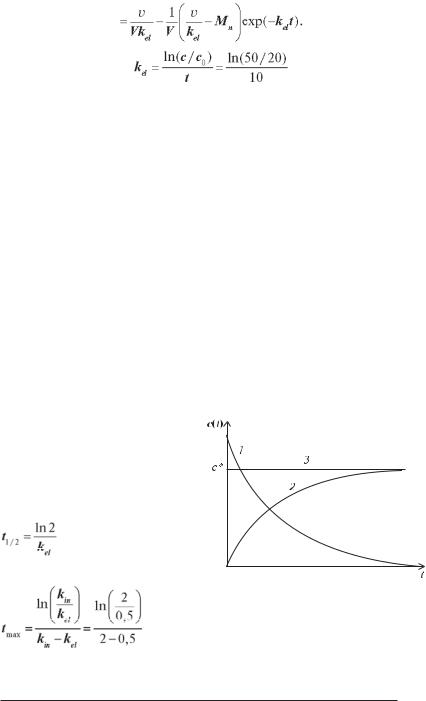
(2.18) Так як при t→∞ множник exp(–kelt)→0, то кінцева концентрація препарату буде як і раніше дорівнювати с* = v/Vkel, тобто не буде залежати від Мn. Концентрація наблизиться до с*, якщо другий доданок у рівнянні (2.18) буде дорівнювати нулю, а це, у свою чер-

(рис. 2.16, крива 3). Звідси можна одержати вираз для навантажувальної

дози (M*), при введенні якої необхідний рівень концентрації препарату

n

буде досягнутий миттєво:

M*= v/k = c*V.

n el

Таким чином, дана модель дозволила визначити миттєву наван-

тажувальну дозу ліків M * і швидкість його введення v в організм. Ці

n

результати були підтверджені експериментально.

Приклади розв’язання задач

Задача 2.1. Початкова концентрація в крові деякого препарату дорівнювала 50 мкг/мл, а через 10 годин зменшилася до 20 мкг/мл. Вважаючи, що даний процес описується однокамерною моделлю, розрахувати константу елімінації цього препарату і час його напіввиведення.

Розв’язання. Константу елімінації обчислимо з лінеаризованого рівняння для концентрації (lnc

= lnc0 – kelt):

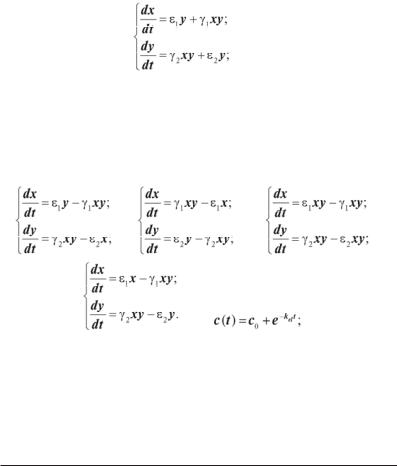
дено внутрішньом’язово 220 мг препарату. Обчислити час, протягом якого концентрація цього препарату в крові досягне свого максимального значення, а також концентрацію препарату в крові через 3 години після введення. Константи всмоктування і виведення рівні відповідно 2 1/год і 0,5 1/год. Уявний об’єм крові прийняти рівним 4,5 л.

Розв’язання. Так як препарат вводиться не безпосередньо в кров, а в іншу тканину, то даний процес буде описуватися моделлю з підкамерою. Час досягнення максимальної концентрації обчислимо з рівняння (2.15):

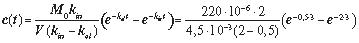= 0,92 год. = 55 хв.

Для обчислення концентрації препарату в довільний момент часу скористаємося рівнянням (2.13):

=

= 14,4·10–3 кг/м3 = 14,4 мкг/мл.

Питання тестового контролю

2.1. Модель хижак — жертва описується такою системою диференціальних рівнянь:

2.2.У моделі хижак — жертва особливі точки відносяться до виду: а) сідло і нестійкий фокус; б) стійкий і нестійкий фокуси; в) стійкий вузол і центр; г) стійкий і нестійкий вузли; д) центр і сідло.

2.3.Зміна концентрації препарату в крові описується рівнянням:

44

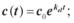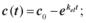а) б) в)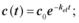

г)

д)

2.4. Час напіввиведення препарату складає:

а)

б)

в)

г)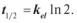

д)

2.5. Препарат вводиться внутрішньом’язово, звідки всмоктується в кров із константою k1, а виводиться з кровоносного русла з константою k2. Складіть диференціальні рівняння, що описують концентрацію препарату в м’язовій тканині (с1) і крові (с2):

2.6. Препарат вводився внутрішньом’язово. Його концентрація в крові в часі t описується таким рівнянням

а)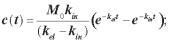

45

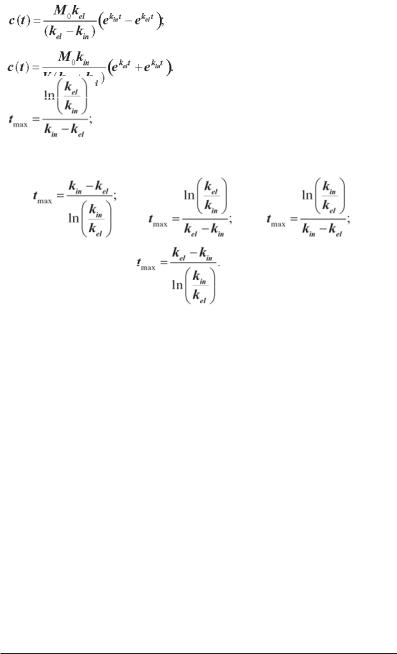
б)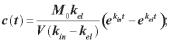

в)

г)

д)

2.7. Препарат вводиться внутрішньом’язово. Час досягнення його максимальної концентрації в крові складає:

2.8. Швидкість, із якою варто вводити препарат, для того, щоб його концентрація в крові була постійною і дорівнювала с складає:

а) v = c 2Vkel ; б) v = cVkel ; в) v = –2cVkel ; г) v = cVkelkin ; д) v = cV 2kel .

2.9.Обчислити час напіввиведення нальбуфіну, якщо константа елімінації для нього складає 0,17 1/год.:

а) 4 год.; б) 0,12 год.; в) 3 доби; г) 20 год.; д) 3 хв.

2.10.Обчислити константу елімінації люміналу, якщо час напіввиведення для нього складає 3 доби:

а) 0,17 1/год.; б) 104 1/год.;

в) 9,6·10–3 1/год.; г) 4,2·10–2 1/год.;

46

д) 3,7·10–2 1/год.

47

Розділ 3. МОЛЕКУЛЯРНА БIОФIЗИКА

Молекулярна біофізика вивчає фізичну структуру біологічно важливих молекул, фізичні процеси, що лежать в основі їхнього функціонування, зв’язок структури і властивостей молекул з їхньою біологічною функцією. Об’єктами дослідження молекулярної біофізики є білки і нуклеїнові кислоти, що формують основу всього живого.

Молекулярна маса білків і нуклеїнових кислот складає від 103 до 1010 а.о.м. Тому їх називають макромолекулами. Білки і нуклеїнові кислоти складаються з великого числа однотипних ланок, білки — з амінокислот, нуклеїнові кислоти — із нуклеотидів.

Всі біологічні макромолекули є динамічними системами. Завдяки можливості поворотів навколо одиничних зв’язків і великої кількості ступенів свободи, кожна молекула має величезну кількість конформацій, однак не усі вони є рівноімовірними через виникаючі невигідні взаємодії атомів, що накладає обмеження на кількість можливих в даних умовах конформацій.

Для дослідження макромолекул використовують безліч фізичних методів: рентгеноструктурний аналіз, ядерноFмагнітний резонанс, спектрофотометрію, ІЧFспектроскопію та ін. Останнім часом, завдяки появі потужної обчислювальної техніки, для вивчення структури макромолекул широко використовуються машинні методи дослідження, які дозволяють розрахувати найбільше вигідні в даних умовах конформації, що відповідають мінімуму потенційної енергії молекули.

§ 14. Види взаємодій у макромолекулах

Зв’язки, що стабілізують біологічні макромолекули, можна умовно розділити на сильні і слабкі. До сильних взаємодій відносяться ковалентні зв’язки, що утворюються при взаємному перекриванні електронних хмар двох сусідніх атомів. Енергія ковалентних зв’язків складає 200–800 кДж/моль, наприклад, енергія С–СFзв’язку дорівнює 348,6 кДж/моль, С–NFзв’язку — 336 кДж/моль.

Однак, як ми побачимо далі, макромолекули не являють собою жорстку застиглу структуру. Навпаки, виконання їхньої біологічної функції неможливе без наявності молекулярної рухливості. Тому, крім сильних ковалентних зв’язків, макромолекули стабілізовані і взаємодіють одні з одними або з надмолекулярними структурами (наприклад, із мембранами) і за допомогою слабких зв’язків, до яких відносяться іонні,

48

іонFдипольні, ванFдерFваальсові, водневі і гідрофобні.

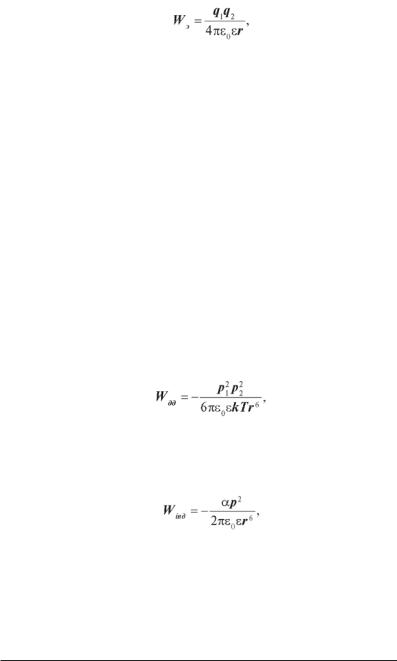
Іонні зв’язки утворюються між зарядженими атомами. Енергія іонного зв’язку визначається за формулою:

де q1, q2 — заряди взаємодіючих іонів; ε0 = 8,85·10–12 Ф/м — електрична стала; ε — відносна діелектрична проникність середовища; r — відстань між іонами.

Багато бічних груп амінокислот, що входять до складу білків, заряджені. Між протилежно зарядженими групами виникають іонні зв’язки, або сольові містки, наприклад, між NH3+Fгрупою лізину і СОО–Fгрупою глутамінової кислоти. Іонні зв’язки також утворюються між позитивно зарядженими фосфатними групами нуклеїнових кислот і катіонами.

Енергія іонного зв’язку залежить від діелектричної проникності середовища. Так у воді (ε = 80) зв’язок буде менш міцним, ніж усередині білкової глобули (ε = 2 ÷ 5). Енергія іонного зв’язку складає від 40 до 400 кДж/моль.

ІонFдипольні взаємодії виникають між іонами і молекулами або атомними групами, що володіють дипольним моментом, наприклад, між іонами і молекулами води. Енергія іонFдипольних взаємодій складає від 4 до 40 кДж/моль.

Атоми, що знаходяться на невеликій відстані один від одного, взаємодіють за рахунок ванFдерFваальсових зв’язків, які включають орієнтаційні, індукційні і дисперсійні взаємодії.

Орієнтаційнізв’язкивиникаютьміжмолекулами,щоволодіютьдипольним моментом. Енергія дипольFдипольної взаємодії має вигляд

(3.1)

де р1, р2 — дипольні моменти взаємодіючих молекул;

k = 1,38·10–23 Дж/К — стала Больцмана; Т — температура.

Молекула,щомаєпостійнийдипольниймомент,здатнаіндукуватийого в сусідній молекулі. Енергія індукційної взаємодії дорівнює

(3.2)

де α — поляризованість молекули або атомної групи.

Енергія орієнтаційних та індукційних зв’язків складає 0,4 — 4 кДж/моль. Формули (3.1) і (3.2) справедливі тільки для точкових диполів.

Дисперсійні взаємодії виникають між нейтральними або неполярними групами і мають квантовомеханічну природу. Їхня енергія визначається в такий спосіб:

49

(3.3) де I1, I2 — потенціали іонізації груп; α1, α2 — поляризованості груп. Енергія дисперсійних зв’язків дорівнює 4–40 кДж/моль.

Водневі зв’язки утворюються між групами, що містять атом водню (О–Н, N–H, F–H, Cl–H і іноді S–H) і атомами O, N, F, S за рахунок електростатичних і ванFдерFваальсових взаємодій. Водневий зв’язок є направленим й утворюється тільки в тому випадку, якщо всі три атоми, що беруть участь у його формуванні, лежать на одній прямій. Енергія водневих зв’язків складає від 4 до 30 кДж/моль. Як ми побачимо далі, водневі зв’язки багато в чому визначають будову і властивості води, грають найважливішу роль у формуванні вторинної структури білків і ДНК.

Гідрофобні взаємодії сприяють відштовхуванню одна від одної неполярних незаряджених груп і молекул води. Ці сили визначають формування структури біологічних мембран і структури глобулярних білків. Докладніше про гідрофобні взаємодії буде розказано нижче.

§ 15. Структура води і гідрофобні взаємодії

Біологічні макромолекули функціонують у водяному середовищі, і їхня просторова будова багато в чому визначається водним оточенням. Тому однією з найважливіших проблем молекулярної біофізики є питання про структуру води.

Воду називають аномальною рідиною. На відміну від інших гідридів VI групи таблиці Менделєєва (H2Po, H2Te, H2Se, H2S) вода має занадто високі температури плавлення і кипіння, а також великий температурний діапазон між цими величинами (відповідно до теоретичних розрахунків, вода повинна плавитися при температурі –95 °С, а закипати при температурі –80 °С, тобто існувати в рідкому вигляді в діапазоні усього лише 15 °С).

При зниженні температури вода, як і всі рідини, стискується, однак цей процес продовжується тільки до 4 °С. Нижче цієї температури вода починає розширятися. Тому максимальна густина води досягається при 4 °С і складає 1·103 кг/м3 (для порівняння, при 0°С густина води вже 0,9167·103 кг/м3). Густина льоду виявляється менше густини води, завдяки чому лід не тоне у воді, а плаває на поверхні. Ця властивість води перешкоджає повному вимерзанню водоймищ взимку і зберігає життя в них. Навіть у найдужчі морози температура придонних шарів не опускається нижче 4 °С.

Вода має аномально високі теплоємність, питому теплоту плавлення і кипіння, діелектричну проникність. Остання величина для води дорівнює

50