
Биофизика 02
.pdf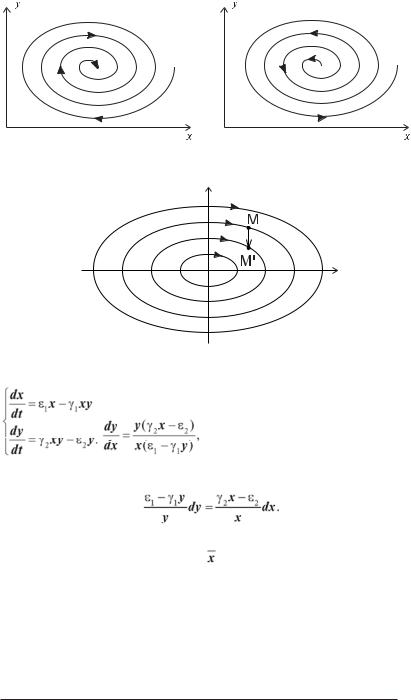
Рис. 2.4. Стійкий (а) та нестійкий (б) фокуси.
y
x
Рис. 2.5. Особлива точка типу “центр”.
Знайдемо рівняння фазових траєкторій, для чого поділимо друге рівняння системи на перше:
(2.5)
або після розділення змінних:
Проінтегрувавши дане рівняння, одержимо:
γ2 x – ε2 ln x + γ1 y – ε1 lny = C, де С — стала інтегрування.
Отримане рівняння дозволяє нам, задаючи значення С, побудувати сімейство фазових траєкторій, але їхній вигляд важко передбачити заздалегідь. Дана задача спроститься, якщо ми знайдемо рівняння ізоклін,
31

координати особливих точок і визначимо їхній тип.
З(2.5) випливають рівняння ізоклін:
x = 0; у = ε /γ ; = 0; х = ε12 /γ12 .у
Для визначення координат особливих точок прирівнюємо чисельник
ізнаменник рівняння (2.5) нулю:
x (ε1 – γ1 y) = 0, γ2 x – ε2) = 0,y (
звідки одержимо:
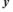 1 = 0,
1 = 0, 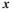 1 = 0;
1 = 0; 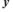 2 = ε2 /γ2,
2 = ε2 /γ2, 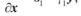 2 = ε1 /γ1.
2 = ε1 /γ1.
Визначимо тип особливих точок, для чого знайдемо наступні часткові похідні:
Тоді для першої особливої точки
З даного рівняння видно, що λ1 > 0, λ2 < 0, що відповідає особливій точці «сідло».
Для другої особливої точки
що відповідає особливій точці типу «центр» (дійсні частини λ дорівнюють нулю).
Тепер можна представити загальну картину розташування фазових траєкторій (рис. 2.6,а). Насправді всі реальні фазові траєкторії розташовуються лише в першому квадранті. Реальний фазовий портрет моделі хижак — жертва наведений на рисунку 2.6,б.
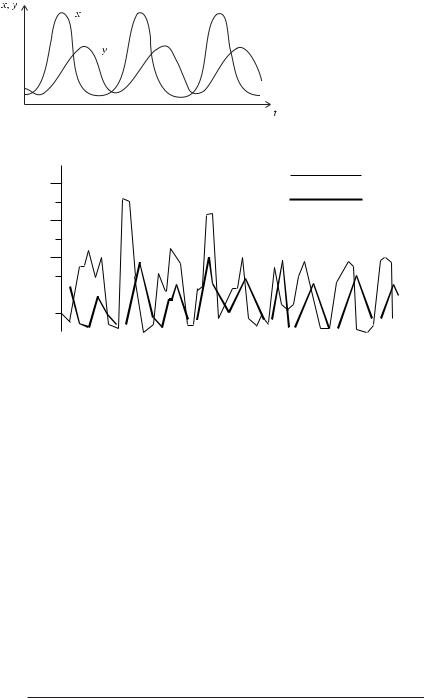
Кожну фазову траєкторію можна розділити на чотири частини, що відповідають різним стадіям взаємодії між хижаками і жертвами (рис.
32
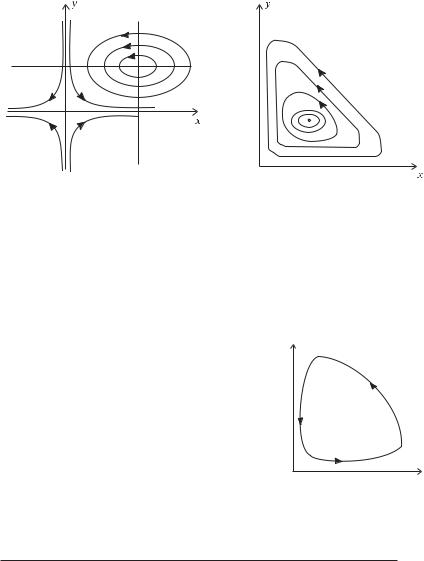
2.7). Як видно з рисунка, на першій стадії кількість жертв зменшується, а кількість хижаків збільшується. Ця стадія називається стадією виїдання жертви. На другому етапі кількість їжі зменшується настільки, що починає зменшуватися популяція хижаків. Це стадія вимирання хижака. На третьому етапі кількість як хижаків, так і жертв така мала, що імовірність їхньої зустрічі вкрай низька. Кількість жертв починає поступово збільшуватися. Це стадія виходу жертв зFпід контролю хижака. На четвертій стадії кількість жертв починає інтенсивно збільшуватися, що викликає
y = ε1 /γ1
х = ε2 /γ2
а |
б |
Рис. 2.6. Фазовий портрет моделі хижак – жертва (пояснення в тексті).
також збільшення, але більш повільне, популяції хижаків. Картина зміни в часі популяцій хижаків і жертв подана на рисунку 2.8.
Модель Вольтерра більшFменш відповідає даним, узятим із статистики чисельностей рисей і зайців у Канаді за різні роки (рис. 2.9), однак для більш точної відповідності в модель уводять ряд поправок.
§ 12. Особливості моделювання фармакокінетичних процесів
Методи математичного моделювання широко застосовують у фармації. При побудові деякої математичної моделі неможливо враховувати всі фактори системи. Математичне моделювання припускає деяке спрощення системи і зневагу деталями, що незначно впливають на процес. Предметом розгляду фармакокінетики є зміна в часі концентрації речовини в клітині, органі, тканині або цілому
y
2
1
3 |
4 |
x
Рис. 2.7. Різні стадії взаємодії хижаків і жертв між собою.
33
Шкурки (тис.)
Рис. 2.8. Залежність чисельності хижаків у і жертв х від часу.
160
120
80
40 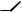
організмі. При цьому звичайно не розглядаються причини зменшення або збільшення концентрації препарату, тобто молекулярні механізми мембранного транспорту, зв’язування і руйнації речовини.
При розгляді цілого
Заєць
Рись
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1845 |
|
|
1865 |
|
|
1885 |
|
|
1905 |
1925 |
|
|
|
Роки |
|||||||||||||||
Рис. 2.9. Криві чисельності зайця і рисі в Канаді.
організму або якогось органа в якості одиниці системи було б розумно вибрати клітину. Однак кількість клітин в організмі і навіть в окремому органі така велика, що розглядати кожну з них неможливо. У фармакокінетиці звичайно за одиницю системи приймається камера. Фармакокінетичною камерою називається частина системи, у якій розподіл препарату можна вважати рівномірним. У залежності від задачі, що розв’язується, за камеру може виступати клітина, орган, тканина і навіть весь організм.
Припущення про рівномірний розподіл препарату в камері з погляду фізіології неприпустиме. Однак якщо перевірка показала адекватність моделі даному процесу, то додаткове введення нових одиниць у розглянуту систему, тобто розбивка фармакокінетичної камери на кілька камер, не буде сприяти підвищенню точності результатів. Введення нових камер може бути обумовлено тільки невідповідністю математичної моделі реальній системі. У залежності від кількості камер фармакокінетичні моделі розділяють на однокамерні, двокамерні та багатокамерні моделі.
34

§ 13. Деякі фармакокінетичні моделі
Припустимо, в організм було введено деякий препарат. Розглянемо модель його виведення з організму. Організм представимо у вигляді посудини А, а навколишнє середовище — у вигляді посудини В (рис. 2.10). Посудина В має нескінченно великий об’єм, тому імовірність проникнення введеного препарату обернено в посудину А мала і з часом увесь препарат переміститься в посудину В. Дана модель є однокамерною, тому що весь організм поданий у вигляді однієї камери.
Можна показати, що зміна кількості препарату в організмі описується наступним експоненціальним рівнянням:
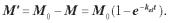 (2.6) де М0 — кількість введеного в організм препарату в початковий момент часу t = 0; М — кількість препарату в організмі в довільний момент часу t; kel — константа швидкості елімінації.
(2.6) де М0 — кількість введеного в організм препарату в початковий момент часу t = 0; М — кількість препарату в організмі в довільний момент часу t; kel — константа швидкості елімінації.
Елімінацією називається сукупність |
|
|
|
|
|
|
|
процесів, що сприяють зменшенню |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
концентрації препарату в організмі. До |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
таких процесів відносяться виведення |
|
|
|
|
|
|
|
|
А |
|
|
|
В |
||
препарату нирками, кишечником, леге- |
|
|
|
|
|||
|
|
|
|
|
|
|
|
нями (у випадку летучих речовин), хімічні |
|
|
|
|
|
|
|
перетворення і необоротне зв’язування, що |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
приводять до втрати біологічної активності. |
Рис. 2.10 (пояснення в тексті). |
Так як М зменшується в часі, то показник |
|
експоненти має знак “мінус”. З (2.6) видно, що на початку процесу препарат буде виводитися швидко, але поступово швидкість цього процесу зменшиться. Сумарна кількість препарату в обох посудинах залишається незмінною, тобто
М + М’ = М0, де М’ — кількість препарату в навколишньому середовищі.
Тоді
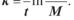 (2.7) З (2.6) і (2.7) випливає, що при t = 0, М = М0, М’ = 0, а при t →∞, навпаки, М = 0, а М’ = М0. Графіки функцій (2.6) і (2.7) приведені на
(2.7) З (2.6) і (2.7) випливає, що при t = 0, М = М0, М’ = 0, а при t →∞, навпаки, М = 0, а М’ = М0. Графіки функцій (2.6) і (2.7) приведені на
рис. 2.11. |
|
Прологарифмувавши (2.6), дістанемо наступне: |
|
ln M = lnM0 – kelt. |
(2.8) |
Дане рівняння дозволяє перейти від експоненціальної залежності до лінійної (рис. 2.12) і обчислити константу швидкості елімінації (або будьFякого іншого процесу), якщо відома початкова кількість речовини
35
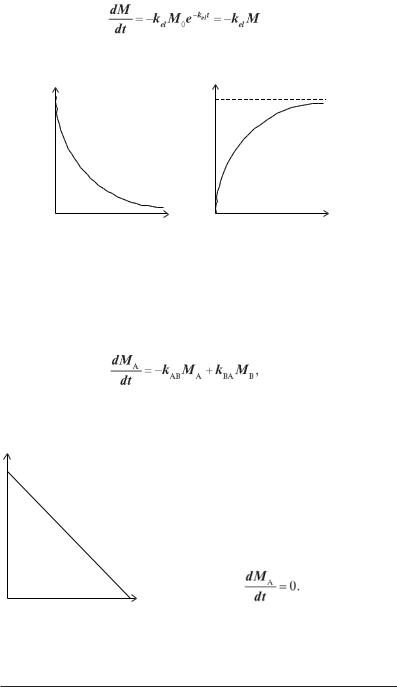
і кількість речовини в деякий момент часу t
Обчислимо миттєву швидкість зміни кількості препарату, для чого продиференціюємо вирази (2.6) і (2.7) за часом. Тоді для деякого моменту
M |
M’ |
M0 |
M0 |
|
а |
t |
б |
t |
Рис. 2.11. Зміна кількості препарату в посудинах А (рис. а) і В (рис. б) у часі.
часу швидкість виведення препарату з однієї камери дорівнює
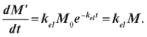 (2.9) і швидкість його накопичення в другий
(2.9) і швидкість його накопичення в другий
Розв’язком отриманих диференціальних рівнянь є вирази (2.6) і (2.7).
Припустимо, що перегородка між камерами А і В пропускає препарат в обидві сторони, але з різною швидкістю (за посудини А і В тут виступають не організм і навколишнє середовище, а, наприклад, орган і кров). У цьому випадку кількість препарату в камері А не буде дорівнювати кількості цього препарату в камері В. Рівняння язміни кількості препарату в камері А прийме вигляд:
t
Рис. 2.12. Залежність кількості препарату в посудині А від часу в
напівлогарифмічних координатах.
де М А і М В — в і д п о в і д н о , к і л ь - кості препарату у камерах А та В;
kАВ — константа швидкості переносу препарату з камери А в камеру В; kВА — конс-
36

танта швидкості переносу препарату з камери В в камеру А.
Через деякий проміжок часу між камерами встановиться рівновага, тобто концентрація препарату не буде змінюватися в часі:
З цієї умови випливає рівність
де  і — кількості речовини в камері А і В, відповідно, після настання рівноваги. З останнього рівняння можна одержати вираз для константи рівноваги К:
і — кількості речовини в камері А і В, відповідно, після настання рівноваги. З останнього рівняння можна одержати вираз для константи рівноваги К:
Від кількості препарату М зручніше перейти до його концентрації
с: |
|
M(t) = Vс(t), |
(2.10) |
де V — уявний об’єм розподілу препарату. Уявний об’єм не відповідає реальному об’єму тканини, а є лише коефіцієнтом пропорційності між кількістю препарату і його концентрацією в тестFтканині 1 . Величину V можна обчислити, розділивши кількість препарату в будьFякий момент часу на концентрацію в цей же момент. Зручніше V обчислювати при t = 0:
Якщо весь уведений препарат поступає у розглянуту камеру, то М0 дорівнює дозі препарату.
Підставимо (2.10) у (2.9):
Скоротивши на постійну величину V, отримаємо
Розв’язок цього рівняння
lnc = lnc – k t, |
(2.11) |
або
Важливим параметром процесу є період напіввиведення препарату t1/2, тобто час, протягом якого концентрація препарату в камері зни-
1 Тест[тканина – тканина, у якій визначається концентрація препарату в ході дослідження.
жується вдвічі. Підставимо в рівняння (2.11) замість концентрації c
Найчастіше тест[тканиною є кров.
37
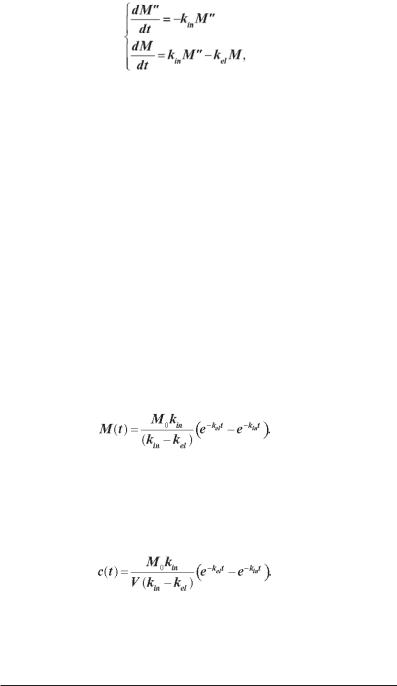
концентрацію c0 /2:
,
звідки отримаємо
Іншим параметром, що характеризує процес, є кліренс Cl, який дорівнює об’єму тестFтканини, що звільняється від препарату за одиницю часу. Ця величина дорівнює добутку уявного об’єму на константу елімінації
Cl = Vkel.
Критерієм застосовності одночастинної моделі для вивчення фармакокінетики препарату є можливість лінеаризації даних у координатах «lnc – t», «dc/dt – c» або «lndс/dt – t».
Лікарські препарати часто вводять не безпосередньо в кров, а в інші тканини. Але як тестFтканина, як і раніше використовується кров. У цьому випадку концентрація препарату в крові досягає максимального значення не відразу, а лише через деякий час. Тому графік залежності концентрації препарату від часу в напівлогарифмічних координатах має лінійний характер лише після досягнення максимальної концентрації (рис. 2.13).
Для таких процесів крім основної камери, що моделює кров та інші тканини, у які проникає препарат, вводять підкамеру, що моделює тканину — місце введення препарату. Для опису такого процесу вже потрібна система з двох рівнянь:
(2.12) де М’’ і М — кількість препарату в підкамері й основній камері відповідно; kin — константа усмоктування препарату з підкамери в основну камеру; kel — константа елімінації препарату з основної камери.
Проінтегрувавши (2.12) з урахуванням початкових умов (М’’(0) = М0, М(0) = 0), одержимо рівняння зміни кількості препарату в основній камері:
Так як M = cV,
де c — концентрація препарату в основній камері; а V — її уявний об’єм, то залежність концентрації від часу має наступний вигляд:
38

(2.13) Знаючи параметри kin, kel, V і М0, по рівнянню (2.13) можна розраху-
вати концентрацію препарату в будьFякий момент часу. Введемо позначення
Тоді рівняння (2.13) запишеться у вигляді:
(2.14)
Увипадку, коли усмоктування препарату відбувається набагато швидше його виведення (kin >>kel), при великих значеннях t членом рівняння ехр (–kint) можна зневажити. Тоді рівняння (2.14) спрощується:
Уцьому випадку низхідна частина залежності (рис. 2.13) характеризує в основному елімінацію препарату. Якщо ж, навпаки,
швидкість усмоктування набагато менша швидкості виведення (kin << kel), рівняння (2.14) зводиться до вигляду:
анизхідна частина кривої характеризує в основному процес усмоктування.
Якщо ж константи усмоктування і виведення мають однаковий порядок, то обидві частини кривої характеризують як елімінацію препарату, так і всмоктування його.
Знайдемо час tmax, протягом якого досягається максимальна концентрація сmax, для чого продиференціюємо вираз 2.14:
Щоб знайти максимальне значення функції, прирівняємо цей вираз нулю
звідки знайдемо tmax:
39

(2.15) З останнього рівняння видно, що час досягнення максимальної концентрації не залежить від дози введеного препарату, а цілком визначається
константами усмоктування і виведення. Підставивши (2.15) у (2.13), мож- |
|||||||||||||||
C, мкг/мл |
|
|
|
|
|
|
|
|
|
|
на визначити максимальну |
||||
|
|
|
|
|
|
|
|
|
|
концентрацію препарату в |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
основній камері. |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для багатокамерних мо- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
делей потрібно складати |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
систему з кількох диферен- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ціальних рівнянь. Концен- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
трація препарату в якомусь |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
органі залежить від швид- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
костей кількох процесів, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кожний із яких характери- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зується власною констан- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тою k: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) від швидкості всмок- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тування препарату з міс- |
0 1 |
2 |
3 |
4 |
5 |
t, год |
ця введення (наприклад, з |
|||||||||
Рис. 2.13. Апроксимація даних фармакокінетики це- |
кишечника) у кров, якщо |
||||||||||||||
фалексину в сироватці крові мишей, які одержували |
було відсутнє безпосереднє |
||||||||||||||
препарат усередину в дозі 400 мг/кг, однокамерною |
введення ліків в кровоносне |
||||||||||||||
|
|
моделлю з усмоктуванням (kin = |
|
русло (константа k12 ); |
|||||||||||
|
|
= 4,60 1/год., kel = 0,90 1/год.). |
|
||||||||||||
|
|
|
2)відшвидкостітранспор- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ту препарату з крові в орган
(константа k23 );
3)від швидкості зворотного процесу: транспорту препарату з органа
вкров (константа k32 );
4)від швидкості виведення препарату з організму видільною систе-
мою (константа k4 ).
Кожний орган, у якому може знаходитися препарат (кишечник, кров, органFмішень, видільні органи) представимо у вигляді окремих блоків (камер) (рис. 2.14), у кожному з яких розподіл препарату однорідний.
На даному етапі вже можна скласти систему диференціальних рів-
40
