Биофизика 02

моль.

Зміна електрохімічного потенціалу позитивна, тобто даний процес невигідний і може відбуватися тільки за рахунок притоку енергії, у даному випадку — за рахунок енергії АТФ.

Задача 1.2. Синтез сахарози здійснюється за наступною схемою: Глюкоза + фруктоза + АТФ →Сахароза + АДФ + Ф,

∆G 0 = –6,3 кДж/моль. Знайти константу рівноваги цієї реакції.

Розв’язання. Зміна вільної енергії в ході хімічної реакції зв’язана з константою хімічної рівноваги K цієї реакції в такий спосіб

∆G 0 = –RT lnK,

звідси

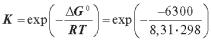= 12,7.

Задача 1.3. Обчислити ефективність спряження синтезу сахарози з реакцією гідролізу АТФ (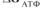 = –30,5 кДж/моль), використовуючи схему попередньої задачі.

Розв’язання. Ефективність спряження визначається як відношення корисної роботи даному випадку енергії, яку необхідно затратити на синтез сахарози 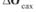) до витраченої роботи ():

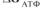= 0,79. Таким чином, ефективність спряження складає 79%.

Питання тестового контролю

1.1. Система знаходиться в стаціонарному стані. При цьому:

а) термодинамічні параметри постійні в часі й однакові у всіх частинах системи, система відкрита або закрита;

б) термодинамічні параметри не змінюються в часі, але можуть відрізнятися в різних частинах системи, система ізольована;

в) у системі підтримуються постійні градієнти параметрів, система відкрита або закрита;

г) термодинамічні параметри постійні в часі й однакові у всіх частинах системи, система ізольована;

д) термодинамічні параметри змінюються в часі, система відкрита. 1.2. Термодинамічний потенціал Гельмгольца визначає корисну

роботу процесу, що протікає при постійних: а) об’ємі й ентропії;

21

б) об’ємі і температурі; в) об’ємі і тиску; г) тиску і температурі; д) тиску й ентропії.

1.3.Термодинамічний потенціал Гіббса визначає корисну роботу процесу, що протікає при постійних:

а) об’ємі й ентропії; б) об’ємі і температурі; в) об’ємі і тиску; г) тиску і температурі; д) тиску й ентропії.

1.4.Осмотична робота, що робиться системою при зміні концентрації від с1 до с2, складає:

а) zF (c2 – c1); б) PV (c2 – c1); в) RT (c2 – c1); г) pV (c2 /c1); д) RТ ln(c2 /c1).

1.5. Електрична робота, що робиться системою при переносі речовини з області з електричним потенціалом ϕ1 в область із потенціалом ϕ2, складає:

а) zF (ϕ2 – ϕ1); б) RT ln(ϕ2/ϕ1);

в) PV (ϕ2 – ϕ1); г) RT ln(ϕ2 – ϕ1);

д) PV (ϕ2/ϕ1).

1.6.Зміна стандартної вільної енергії в ході хімічної реакції зв’язана

зконстантою хімічної рівноваги K цієї реакції в такий спосіб:

а) ∆G 0 = cRK 3;

б) ∆G 0 = –RT lnК; в) ∆G 0 = –RT∆K; г) ∆G 0 = mRK 2; д) ∆G 0 = RK∆T.

1.7. Для хімічних реакцій швидкість продукції ентропії складає:

а)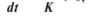

б)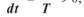

в)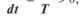

22

г)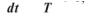

д)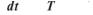

де А — спорідненість хімічної реакції; v — її швидкість; К — константа хімічної рівноваги.

1.8. Критерієм можливості спряження двох і більше процесів є наступна умова:

а)

б)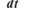

в)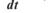

г)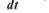

д)

1.9.Зміна стандартної вільної енергії в процесі гідролізу АТФ скла-

дає:

а) –17,3 кДж/моль; б) 60,5 кДж/моль; в) –3 кДж/моль; г) 12,3 кДж/моль; д) –30,5 кДж/моль.

1.10.Зміна вільної енергії в процесі переносу двох електронів від відновленого нікотинамідаденіндинуклеотиду на кисень складає –220 кДж/моль. Цей процес спряжений із синтезом трьох молекул АТФ. Обчислити ефективність спряження:

а) 42%; б) 65%; в) 87%; г) 100%;

д) ці процеси взагалі не можуть бути спряжені.

23

Розділ 2. МАТЕМАТИЧНА БIОФIЗИКА

Математична біофізика вивчає біологічні системи, використовуючи для цього математичні методи. Багато процесів у біології та хімії можна описати за допомогою диференціальних рівнянь або їхніх систем, причому опис як хімічних, так і біологічних процесів вимагає використання подібних математичних методів. Нижче будуть розглянуті випадки застосування методів математики в біології і хімії на прикладі взаємодії біологічних видів між собою і кінетики розподілу лікарського препарату в організмі.

§8. Модель хижак — жертва

У1931 р. італійський математик В. Вольтерра побудував математичну модель взаємодії видів, так звану модель хижак — жертва.

Припустимо, що в одному районі живуть зайці (жертви) і рисі (хижаки). Позначимо чисельність зайців x, а чисельність рисей — y. Зайці харчуються рослинною їжею, наявною в достатку, тому швидкість їхнього розмноження залежить тільки від їхнього числа:

vрозм = ε1x,

де ε1 — коефіцієнт пропорційності.

Необмежене розмноження зайців неможливе, тому що в них є природні вороги. Дана модель припускає, що з безлічі імовірних хижаків є тільки один, наприклад, рисі. Зменшення кількості зайців буде тим скоріше, чим більше імовірність їхньої зустрічі з рисями, а ця імовірність, у свою чергу, пропорційна чисельності як рисей, так і зайців. Тоді швидкість зменшення кількості зайців описується наступним рівнянням:

vзмен = γ1xy,

де γ1 — коефіцієнт пропорційності. Таким чином, рівняння загальної швидкості зміни чисельності зайців має наступний вигляд:

dx/dt = ε1x – γ1xy.

Природною смертю зайців ми зневажаємо, вважаючи такі випадки дуже рідкими.

Швидкість розмноження рисей залежить від наявності їжі (зайців), тобто також визначається імовірністю їхньої зустрічі (константа γ2). Зменшення чисельності рисей пояснюється їхньою природною смерт-

25

ністю і пропорційне їхній чисельності (константа ε2). Тоді для швидкості зміни чисельності рисей можна записати:

∂y/ ∂t = γ2xy – ε2y.

Розглядаються дві перемінні, тому зручно ввести систему координат і на координатній площині відзначати точки, що відповідають певним значенням х та у. Кожна така точка М(х, y) відповідає певному стану системи і називається зображуючою або представляючою, а координатна площина — фазовою площиною. Значення х та у змінюються в часі, і, отже, змінюється положення зображуючої точки. Її рух по фазовій площині називається фазовою траєкторією, або інтегральною кривою.

Значення х та у мають певний біологічний або хімічний зміст (чисельність осіб, концентрація речовини). Як правило, вони не можуть приймати негативні значення, тому область їхніх значень лежить у першій координатній чверті.

Кожному набору параметрів відповідає своя фазова траєкторія, тобто кожна фазова траєкторія описує всі можливі стани системи при постійних значеннях параметрів (констант). По теоремі Коші, через кожну точку фазової площини може проходити тільки одна фазова траєкторія. Фазова площина є сукупністю усіх фазових траєкторій. Для реальних систем значення параметрів коливаються у вузькому діапазоні, і фазові траєкторії займають тільки частину фазової площини. Зображення реальних фазових траєкторій на фазовій площині називається фазовим портретом системи.

Отриману раніше систему диференціальних рівнянь у загальному вигляді можна записати як

(2.1) Так як праві частини обох рівнянь не залежать явно від часу, то, розділивши одне рівняння на інше, ми одержимо диференціальне рівняння,

що не містить час t у явному вигляді

(2.2) Розв’язок цього рівняння має вигляд у = f ( x, C ), де С — стала інтегрування. Вирішивши рівняння, ми одержали б сімейство інтегральних кривих. Однак це вдається дуже рідко, тому що в загальному вигляді дане рівняння розв’язку не має. Для побудови фазового портрета звичайно

застосовують якісні методи. Одним із них є метод ізоклін.

26

§ 9. Метод ізоклін

Ізоклінами називаються лінії, що перетинаються інтегральними кривими під тим самим кутом. Так як існує нескінченна безліч кутів, то існує нескінченна безліч ізоклін.

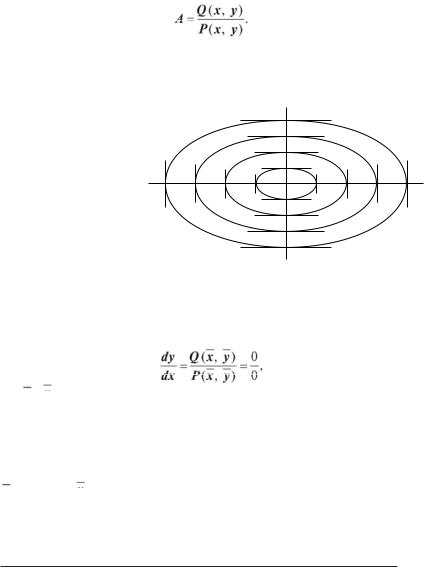
Для одержання рівнянь ізоклін використовують рівняння (2.2). Якщо dy/dx = A, де А — певна постійна величина, то А буде тангенсом кута нахилу дотичної до фазової траєкторії. Тоді рівняння ізокліни буде мати вигляд:

Для одержання фазового портрета потрібно побудувати щонайменше дві ізокліни. Звичайно вибираються так звані головні ізокліни: вони перетинають інтегральні криві в точках, дотичні в яких нахилені під кутом 0° і 90° до координатних осей (рис.

2.1). У випадку, коли dy/dx = 0 (tg α = 0, α = 0°), отримана ізокліна

є ізокліною горизонтальних дотичних до фазових траєкторій,

її рівняння Q(x, y) = 0. Якщо dy/dx = ∞ (tg α = ∞, α=90°), то ми маємо ізокліну вертикальних дотичних, рівняння якої Р (x, y) = 0.

Існує точка, у якій одночасно перетворюються в нуль похідні по х і по у. Ця точка називається особливою. Для неї виконується умова:

де (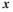, 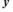) — координати особливої точки.

З рівняння (2.2) можна визначити єдину дотичну до даної інтегральної кривої. Але так як в особливій точці похідна не визначена, то в ній неможливо визначити напрямок дотичної. Тому в особливій точці перетинаються всі ізокліни.

У випадку, коли dx/dt =dy/dt =0, х та у приймають постійні значення, 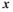(t) =const, 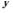(t) =const. Такий стан системи називається стаціонарним або станом рівноваги. Кількість стаціонарних станів визначається чис-

лом перетинань головних ізоклін або двох будьFяких інших ізоклін.

27

§ 10. Стійкість стаціонарного стану та види особливих точок

Стаціонарні стани й відображаючі їх графічно особливі точки бувають стійкими і нестійкими. Якщо система, виведена зі стаціонарного стану, самочинно повертається в нього, то такий стан називається стійким, якщо ж при відхиленні від стаціонарного стану виникають сили, що ще більш відхиляють точку від рівноваги, то — нестійким.

Розглянемо метод Пуанкаре і Ляпунова для дослідження стійкості стаціонарного стану. Припустимо, що система вийшла зі стану рівноваги. Її нове положення на фазовій площині буде визначатися координатами

х = 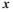+ ξ; у = 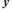+ η,

де ξі η— зсув зображуючої точки від положення рівноваги, координати якого ( x , y ). Підставивши нові координати в систему рівнянь (2.1), одержимо наступні рівняння:

де d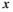/dt = d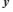/dt = 0, тому що і — постійні величини. Розкладемо праві частини отриманих рівнянь у ряд Тейлора за змін-

ними ξ і η і відкинемо нелінійні члени. Тоді система прийме вигляд:

(2.3)

де

Ми одержали так звану лінеаризовану систему або систему першого наближення.

Дана система називається “грубою”, тому що для неї при малих змінах вигляду вихідних рівнянь не змінюється характер фазових траєкторій. Для таких систем досить досліджувати лінеаризовані рівняння, щоб довідатися, чи буде даний стан рівноваги стійким. Крім того, дослідження цих рівнянь дозволяє визначити характер фазового портрета в окрузі особливої точки.

Загальний розв’язок системи (2.3) знаходять у вигляді:

28

Для того, щоб система рівнянь була невиродженою, тобто мала ненульовий розв’язок, її визначник повинен дорівнювати нулю:

або

λ2 – (a + d)λ + (ad – bc) = 0 .

Отримане в такий спосіб рівняння називається характеристичним. Розв’язок його має наступний вигляд:

(2.4)

Зурахуванням (2.4) загальний розв’язок системи (2.3) буде записано

увигляді:

поблизу положення рівноваги, і, отже, про характер і напрямок фазової траєкторії. У залежності від значень λ1 і λ2, що визначають ξ і η, існує кілька видів особливих точок.

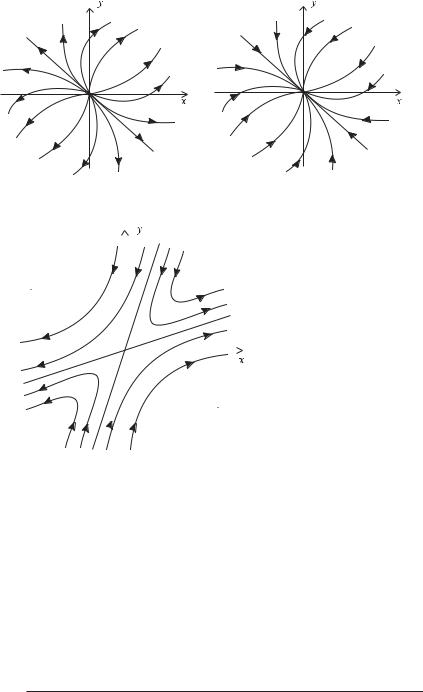
У випадку коли λ1 і λ2 дійсні і додатні, особлива точка називається хитливим вузлом (рис. 2.2,а). Фазові траєкторії в цьому випадку виходять із неї. Така рівновага є нестійкою, тому що, якщо з якоїсь причини система була виведена з рівноваги, то вона вже не може самочинно повернутися в неї. Якщо ж λ1 і λ2 дійсні і від’ємні, то маємо стійкий вузол (рис. 2.2,б), у якому фазові траєкторії сходяться. Такий стан стійкий і, якщо система, виведена з рівноваги, не вийшла з області впливу даної особливої точки, то, надана самій собі, вона знову повернеться до рівноваги.

Якщо корені характеристичного рівняння дійсні, але різних знаків, то особлива точка зветься “сідлом” (рис. 2.3). Такий стан завжди нестійкий.

Якщо підкореневий вираз в рівнянні (2.4) від’ємний, то λ1 і λ2 є комплексними числами. У цьому випадку особлива точка називається фокусом, а фазові траєкторії мають форму спіралей. Стійкість або нестійкість фокуса визначається знаком дійсної частини λ1 і λ2: якщо вони від’ємні, то фокус стійкий, якщо додатні — нестійкий (рис. 2.4, а і б).

Тип особливих точок, називаний центром, зустрічається, коли дійсна частина λ дорівнює нулю. Інтегральні криві в цьому випадку мають

29

Рис. 2.2. Стійкий (а) та нестійкий (б) вузли.

коливання з декілька меншою амплітудою, але самочинно наближатися до особливої точки не буде.

§ 11. Аналіз моделі хижак — жертва

Дослідимо за допомогою вищеописаних методів модель хижак — жертва, що описується системою рівнянь

30