Биофизика 02

кооперативний характер, тобто, чим більше ліпідів зробило фазовий перехід, тим легше це буде зробити іншим. В ідеалі, якщо на якійсь ділянці одна молекула ліпіду перейшла з твердого в рідиннокристалічний стан, то відразу ж здійсниться фазовий перехід усіх ліпідів цієї ділянки (закон «усе або нічого»). Таку ділянку називають кооперативною одиницею, а число молекул, що входять до неї — розміром кооперативної одиниці. Для ліпідних мембран ця величина може досягати декількох десятків. Розмір кооперативної одиниці тим більший, чим більший однорідний хімічний склад мембран. Для зменшення одноманітності ліпідного складу мембрани тваринних клітин містять велику кількість холестерину, наприклад, в еритроцитах ссавців його питома частка від усіх ліпідів складає від 40 до 60%. Це значно зменшує розмір кооперативної одиниці і знижує різницю між твердою і рідкою фазами.

Одним з найбільш поширених методів вивчення фазових переходів у мембранах є метод мікрокалориметрії, який дозволяє визначити кількість теплоти ∆Q, поглинену при плавленні речовини, що містить ν молей молекул. Знаючи ∆Q, можна розрахувати питому ентальпію плавлення:

(4.4)

Ця величина приблизно однакова для кожної групи СН2 і складає 4,8·10–24 Дж/К, тоді для моля СН2Fгрупи вона дорівнює 2,9 Дж/К. Таким чином, чим довші вуглеводневі ланцюги жирнокислотних залишків, тим більша зміна ентропії, що приходиться на один моль молекул.

Відомо, що

де k — стала Больцмана; W — термодинамічна імовірність, або кількість можливих мікростанів системи, що відповідають тому самому макростану. Це рівняння дозволяє знайти зміну кількості мікростанів однієї СН2Fгрупи при фазовому переході. Якщо в рідиннокристалічному стані кількість мікростанів рівнялась W1, а в гельFстані — W2, то зміна ентропії при фазовому переході складе

звідки

91

(4.9) Тут ∆S <0, тому що при переході в більш упорядкований твердокристалічний стан ентропія зменшується. Таким чином, під час кристалізації число можливих мікростанів СН2Fгрупи зменшується майже в півтора

рази.

Приклади розв’язання задач

Задача 4.1. Розрахувати товщину мембрани, якщо її ділянка площею 1 мкм2 має електричну ємність, рівну 0,7·10–14 Ф. Діелектрична проникність ліпідів дорівнює 2.

Розв’язання. З формули для ємності електричного конденсатора

знайдемо товщину мембрани d

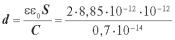= 5·10–9 м = 5 нм.

Задача 4.2. Розрахувати коефіцієнт латеральної дифузії фосфоліпідів, якщо середній час їхнього осілого життя складає 3,3·10–8 с. Площа, що займається одною молекулою на мембрані, складає 7·10–19 м2.

Розв’язання. Час осілого життя обернено пропорційний частоті перескоків молекул на мембрані внаслідок латеральної дифузії

звідки одержуємо D

= 6,1·10–12 м2/с.

Питання тестового контролю

4.1.Товщина біологічних мембран складає порядку: а) 0,01 нм; б) 0,1 нм; в) 10 нм; г) 100 нм; д) 1 мкм.

4.2.Відповідно до рідинноFмозаїчної моделі, біологічна мембрана складається з:

92

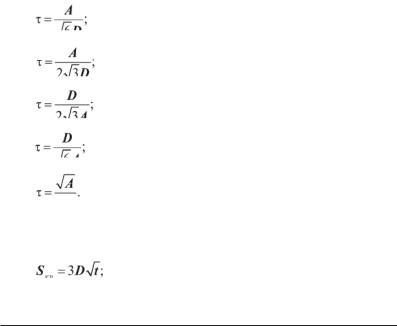
а) біліпідного шару; б) двох шарів ліпідів із білковим шаром між ними;

в) двох шарів ліпідів, оточених зверху і знизу двома суцільними білковими шарами;

г) біліпідного шару, білків і мікрофіламентів; д) шару ліпідів із украпленнями білків і вуглеводів. 4.3. Латеральною дифузією називається:

а) дифузія ліпідів та білкових молекул з одного ліпідного шару в інший;

б) дифузія ліпідів та білкових молекул через біомембрану; в) дифузія ліпідів та білкових молекул у мембрані в межах одного

шару; г) дифузія білкових молекул з одного білкового шару в інший;

д) дифузія іонів через бішарову мембрану. 4.4. “ФліпFфлоп”Fпереходом називається:

а) дифузія ліпідів та білкових молекул з одного ліпідного шару в інший;

б) дифузія ліпідів та білкових молекул через біомембрану; в) дифузія ліпідів та білкових молекул у мембрані в межах одного

шару; г) дифузія білкових молекул з одного білкового шару в інший;

д) дифузія іонів через бішарову мембрану.

4.5. Час осілого життя молекули в одному положенні складає:

а)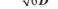

б)

в)

г)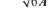

д)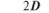

4.6. Середнє квадратичне переміщення молекул за час t складає: а)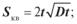

б)

93

в)

г)

д)

4.7. Ліпосомами називаються:

а) мономолекулярні шари на межі поділу гідрофобної і гідрофільної фази;

б) плоскі бішарові ліпідні мембрани; в) біліпідні замкнуті структури;

г) шари ліпідів і білків, нанесені на поверхню води; д) те ж саме, що і міцели.

4.8.Ліпіди в складі біологічних мембран знаходяться в: а) твердому аморфному стані; б) твердокристалічному; в) рідкому аморфному стані;

г) рідиннокристалічному стані.

4.9.При фазовому переході мембрани з рідкого в гельFстан площа мембрани, що приходиться на одну молекулу ліпіду:

а) зменшується; б) збільшується; в) не змінюється.

4.10.При фазовому переході мембрани з рідкого в гельFстан товщина мембрани:

а) зменшується; б) збільшується; в) не змінюється.

4.11.Чим більше в хвостах ліпідів подвійних зв’язків, тим температура фазового переходу:

а) вища; б) нижча;

в) не залежить від цього.

4.12.Температура плавлення мембрани зв’язана зі зміною ентальпії

йентропії в цьому процесі в такий спосіб:

а)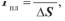

б)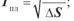

в)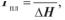

94

г)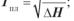

д)

4.13.Розрахувати діелектричну проникність мембранних ліпідів, якщо товщина мембрани складає 10 нм, питома електрична ємність дорівнює 1,7·10–3 Ф/м2:

а) 10; б) 80; в) 0,78; г) 54; д) 2.

4.14.Розрахувати середнє квадратичне переміщення молекул білків за 1 с, якщо коефіцієнт латеральної дифузії для них складає приблизно 10–14 м2/с.

а) 2,8·10–7 м; б) 0,2 мкм; в) 0,8 мкм; г) 3·10–14 м; д) 5 мкм.

95

Розділ 5. ТРАНСПОРТ РЕЧОВИН КРIЗЬ БIОЛОГIЧНI МЕМБРАНИ

Більшість процесів життєдіяльності, таких як всмоктування, виділення, проведення нервового імпульсу, м’язове скорочення, синтез АТФ зв’язані з перенесенням речовин через мембрани. Цей процес у біологічних системах одержав назву транспорту.

Якщо перенесення речовини відбувається зі зменшенням градієнта електрохімічного потенціалу, тобто не вимагає витрат енергії, то такий транспорт називається пасивним. Його різновидами є дифузія (переміщення речовин убік меншої концентрації) і фільтрація (просочування речовин через пори убік менших значень тиску). За допомогою дифузії в клітину проникають вода, розчинені молекули кисню і вуглекислого газу, а також не властиві організму сполуки, наприклад, лікарські препарати і отрути. Фільтрація забезпечує перенесення води через стінки кровоносних судин, видавлювання плазми крові в ниркові канальці.

Транспорт речовин через ліпідний бішар за допомогою простої дифузії відбувається з малою швидкістю, особливо у випадку заряджених частинок, і майже не контролюється. Тому в процесі еволюції для деяких речовин з’явилися специфічні мембранні канали і мембранні переносники, що сприяють підвищенню швидкості перенесення і крім того здійснюють селективний (виборчий) транспорт. Пасивний транспорт речовин за допомогою переносників називається полегшеною дифузією.

Іноді потрібно перенести речовину з області з меншим значенням електрохімічного потенціалу в область із більшим його значенням. Цей процес не може протікати спонтанно і вимагає витрат енергії. Такий вид транспорту називається активним. У бік більших значень електрохімічного потенціалу переносяться, наприклад, іони натрію через мембрану клітини. Якщо енергія, необхідна для здійснення активного транспорту, береться за рахунок гідролізу АТФ або окислювальноFвідновлювальних реакцій, то такий транспорт називається первинноFактивним, якщо за рахунок градієнта концентрацій інших іонів, то — вторинноFактивним або спряженим.

Через мембрану можуть переноситися не тільки окремі молекули, але і тверді тіла (фагоцитоз), розчини (піноцитоз). Якщо речовина транспортується усередину клітини, то такий вид транспорту називається ендоцитозом, якщо назовні, то — екзоцитозом. У першому випадку мембрана утворює впячування, що поступово перетворюєть-

96

ся в пухирець, який відривається від мембрани усередині клітини. Такий пухирець (фагоF або піносома) містить усередині речовину, що транспортується, оточену біліпідною оболонкою (везикулою). Надалі везикула зливається з якоюFнебудь клітинною органелою (наприклад, лізосомою) і випускає туди свій вміст. У випадку екзоцитозу процес відбувається в зворотній послідовності: везикула підходить до мембрани з внутрішньої сторони клітини, зливається з нею і викидає свій вміст у міжклітинний простір.

Ефективність більшості ліків залежить від їхньої спроможності перебороти мембранний бар’єр. Цей фактор необхідно враховувати при синтезі нових лікарських сполук.

§ 23. Пасивний транспорт нейтральних частинок

Якщо в двох різних областях простору концентрації тієї самої речовини не рівні (існує градієнт концентрації), то в цьому випадку буде відбуватися дифузія (або пасивний транспорт) цієї речовини з області з більшою концентрацією в область з меншою концентрацією. Це явище буде відбуватися спонтанно (без витрат енергії) доти, поки концентрації речовини не вирівняються і сумарний потік речовини не стане рівним нулю (у випадку живих клітин таке вирівнювання може і не наступити, якщо речовини безупинно синтезуються або, навпаки, затрачуються з якогось боку мембрани).

Дифузія може відбуватися в усіх напрямках у просторі й у кожному напрямку швидкість її може бути різною. Щоб спростити обчислення, виберемо лише один напрямок. Пасивне перенесення речовини уздовж осі х описується рівнянням Фіка:

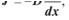(5.1) де J — густина потоку речовини; D — коефіцієнт дифузії; dс/dx — градієнт концентрації в напрямку х. Знак “—“ означає, що потік направлений вбік зниження концентрації, тобто приводить до зменшення концентраційного градієнта.

Густина потоку чисельно дорівнює кількості перенесеної речовини за одиницю часу через одиницю площі поверхні, перпендикулярної напрямку перенесення

де dМ — кількість перенесеної речовини за час dt через площадку площею S. Так як dМ/dt — це швидкість перенесення речовини, то густина потоку прямо пропорційна цій величині. Надалі для спрощення замість

97

терміна «густина потоку» будемо вживати просто «потік».

Розглянемо пасивний транспорт незаряджених частинок через мембрану. Якщо концентрація частинок зовні менша концентрації всередині клітини або навпаки, то на мембрані створюється градієнт концентрацій. У даному випадку його можна вважати постійною величиною, тобто

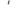де і — концентрація речовини в мембрані біля її меж зовні та всередині1 , відповідно, l — товщина мембрани (рис. 5.1). Підставивши цей вираз в рівняння Фіка (5.1), одержимо:

(5.2 ) Введемо поняття коефіцієнта розподілу речовини між мембраною і

навколишнім середовищем:

(5.3) де сo і сi — концентрація речовини зовні й усередині клітини, відповідно (рис. 5.1). Різниця між і сo, і сi пояснюється різною розчинністю речовини в полярних і неполярних розчинниках. Висловимо і з (5.3):

1 Індекси “i” та “o” походять від англ. inside — усередині та outside — зовні.

98

де см — концентрація речовини в ліпофільному середовищі (олії); св — концентрація цієї ж речовини в гідрофільному середовищі (воді). Чим більше значення К, тим краще речовина розчиняється в мембрані і з тим більшою швидкістю переноситься через неї.

Для нейтральних речовин із приблизно однаковими молекулярними масами і діаметром, але з різним значенням коефіцієнта розподілу це доведено експериментально. Наприклад, коефіцієнт проникності мембрани бичачих еритроцитів для 1,2Fдігідроксіпропану, що має К = 570, у 235 разів вище, ніж для гліцерину, коефіцієнт розподілу якого дорівнює 7. Нагадаємо, що гліцерин відрізняється від 1,2Fдігідроксіпропану наявністю третьої гідроксильної групи, здатної утворювати водневі зв’язки з молекулами води, що значно зменшує ліпофільність і підвищує гідрофільність гліцерину. Швидкість проникнення в клітину ліків також прямо залежить від їхнього коефіцієнта розподілу в неполярному і полярному розчиннику.

При перенесенні одного моля речовини з області, де концентрація цієї речовини дорівнює с1, в область, де її концентрація с2, змінюється вільна осмотична енергія

∆G = RT (ln c2 – ln c1).

Для малих змін концентрацій можна записати:

Розділимо цей вираз на dx:

Висловивши звідси dc/dx і підставивши його в рівняння Фіка (5.1), одержимо:

де — рухливість частинки. Потік, таким чином, прямо пропорційний концентрації і градієнту вільної енергії, а рухливість відіграє роль коефіцієнта пропорційності між цими величинами.

§ 24. Пасивний транспорт іонів

Усе вищевикладене відносилося до незаряджених частинок. Потік частинок, що володіють зарядом q, при наявності градієнта електричного потенціалу dϕ/dx дорівнює

99

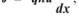(5.4) де n — кількість частинок в одиниці об’єму, u — рухливість частинки.

Вільна електрична енергія одного моля заряджених частинок складає:

∆G = zF (ϕ2 – ϕ1) = zeNA(ϕ2 – ϕ1) = qNA(ϕ2 – ϕ1),

де z — заряд іона в одиницях елементарного заряду; F = NAe — число Фарадея; e — заряд електрона; NA = 6,023·1023 1/моль — число Авогадро. Перейшовши від різниць до диференціалів і розділивши цей вираз на dx, одержимо:

Висловимо звідси dϕ/dx і підставимо його в рівняння (5.4):

де с = n/NA — молярна концентрація.

Таким чином, рівняння для потоків як незаряджених, так і заряджених частинок подібні. У тому випадку, коли змінюється не тільки концентрація речовини та електричний потенціал, але і стандартний хімічний потенціал (µ0), рівняння для потоку речовини записується в такому вигляді (рівняння Теорелла):

Підставивши в це рівняння вираз для електрохімічного потенціалу, отримаємо:

Стандартний хімічний потенціал µ0 залежить від природи розчинника. Якщо у всій розглянутій області дифузії розчинник однаковий, та з речовиною, що транспортується, не відбувається хімічних змін, то dµ0/dx =0. У цьому випадку рівняння Теорелла зводиться до електродифузійного рівняння Нернста — Планка:

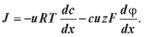(5.5) Це рівняння описує пасивне перенесення частинок в умовах існування градієнтів концентрації речовини й електричного потенціалу в

розчині або в однорідній незарядженій мембрані.

Один зі способів рішення рівняння Нернста — Планка припускає

100