4. Шляхи реалізації цілей заняття:

Для реалізації цілей заняття Вам необхідні такі вихідні знання:

1. сталі та змінні величини;

2. аргумент та функція;

3. означення та інтерпре­тацію похідної функції;

4. таблицю похідних елементар­них функцій;

5. похідні алгебраїчної суми, добутку, частки функцій та похідну складеної функції.

Вам необхідні також вміти обчислювати похід­ні елементарних функцій за допомо­гою таблиці похід­них та відповідних правил.

5. Завдання для перевірки студентами свого вихідного рівня знань.

1. Доведіть рівність .

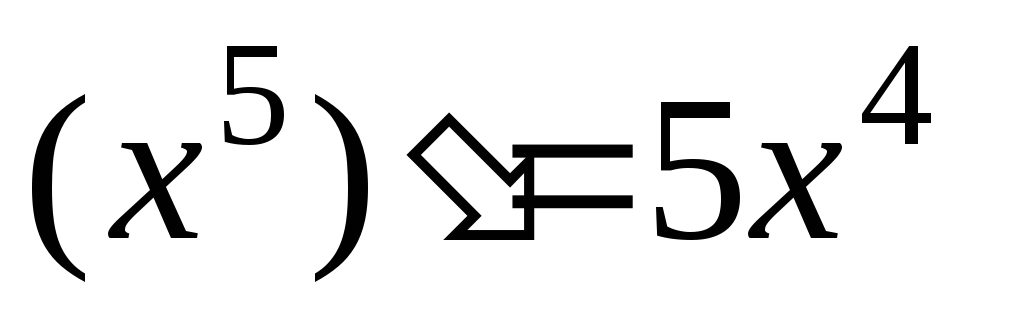2 Знайдіть похідну функції .

(Правильна відповідь ).

3 Знайдіть похідну функції .

(Правильна відповідь ).

4 Знайдіть похідну функції .

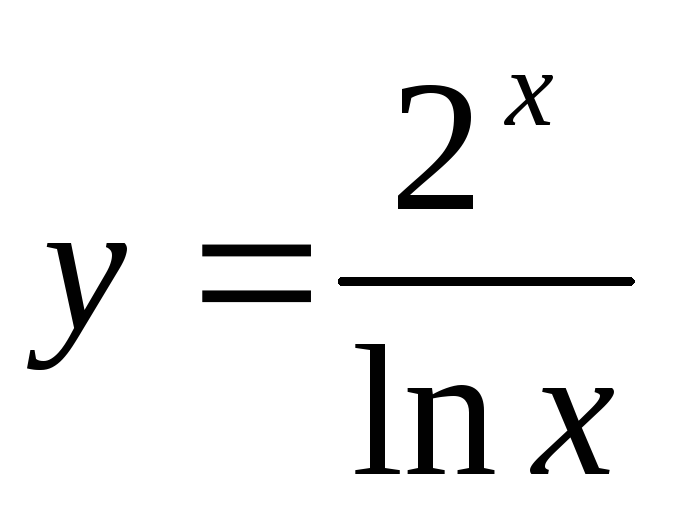(Правильна відповідь ).

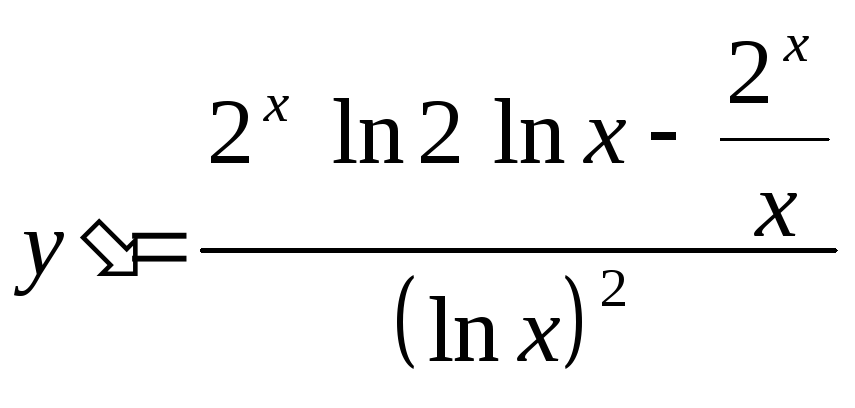5 Знайдіть похідну функції .

(Правильна відповідь ).

6. Інформацію для закріплення вихідних знань-вмінь можна знайти у посібниках:

1. Жуматій П.Г. “Математична обробка медико-біологічних даних. Задачі та приклади”. Одеса, 2009.

2. Жуматій П.Г. “Основи диференціального числення”. Одеса, 2009.

3. Жуматій П.Г. Сеницька Я.Р. Елементи вищої математики. Методичні вказівки для студентів медичного інститута. Одеса, 1981.

7. Зміст навчального матеріалу з даної теми з виділенням основних вузлових питань.

Первісна та невизначений інтеграл

Функція називається первісною для функції, якщоє похідною для.

Сукупність первісних для даної функціїназивається невизначеним інтегралом

,

(читається: " невизначений інтеграл еф від ікс де ікс ").

Термінологія:

•  - знак інтеграла

• x - змінна інтегрування

• - підінтегральна функція

• dx - підінтегральний вираз

• С - стала інтегрування.

Геометрично невизначений інтеграл представляє собою сім’ю кривих, рівняння яких відрізняються одне від одного сталим доданком С, і одержати їх можна паралельним перенесенням вздовж осі ординат.

Основні невизначені інтеграли:

.

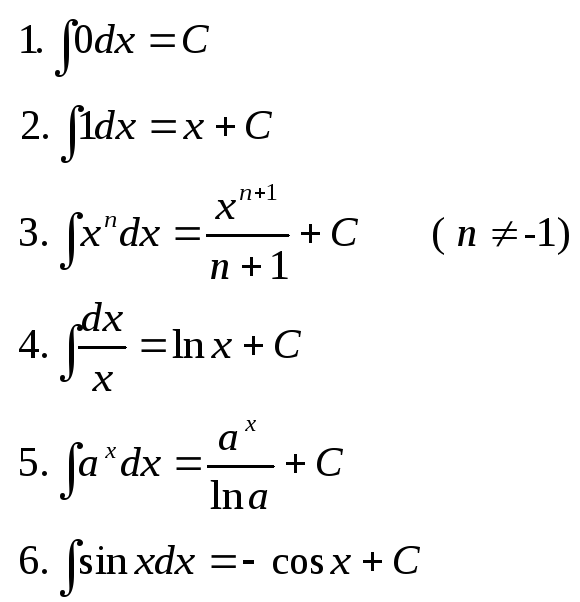
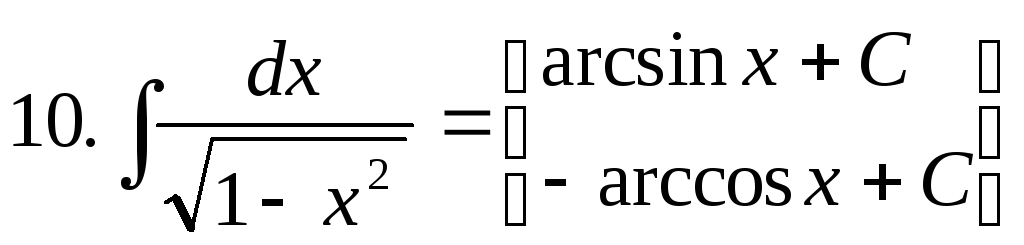
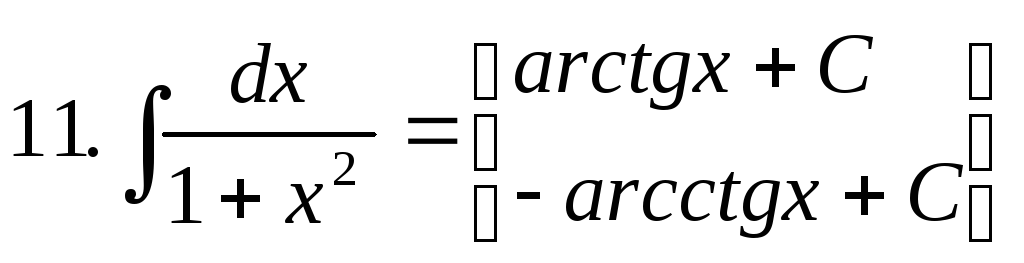
Лінійні властивості операції інтегрування можна виразити однією формулою

,

де a та b - довільні сталі множники.

Визначений інтеграл

y = f(x)

Y B

A

a b X

До необхідності обчисляти визначений інтеграл приводять багато практичних задач, наприклад, обчислення площі S криволінійної трапеції аАВb, обмеженої зверху ділянкою графіка АВ функції (x), а внизу інтервалом [a,b] осі Х. З урахування позначень меж інтервалу (нижньої a та верхньої b) і функції (x), визначений інтеграл записують так

S = ,

( читається: " визначений інтеграл від a до b еф від ікс де ікс").

Термінологія, введена для невизначеного інтеграла, залишається у силі та доповнюється:

• a - нижня межа інтегрування

• b - верхня межа інтегрування

• [a,b] - область інтегрування.

У загальному випадку для обчислення визначених інтегралів застосовують спеціальні методи численного інтегрування. Проте, якщо для підінтегральної функції (x) відома первісна функція , то можна скористатись формулою Ньютона - Лейбніца:

.

Визначений інтеграл застосовують, зокрема, для обчислення середнього значення функції (x) на інтервалі [a,b]:

.