ЭД / Новая папка (2) / DOC / ЛК 2 ТЭД_и_РРВ_ч_2

ЭД и РРВ (ЛК 2)

РАСПРОСТРАНЕНИЕ РАДИОВОЛН

В СВОБОДНОМ ПРОСТРАНСТВЕ

• Поле излучателя, находящегося в свободном пространстве;

• понятие коэффициента направленного действия (КНД);

• поле излучателя, находящегося в свободном пространстве

с учетом КНД передающей антенны;

• поле излучателя, находящегося в свободном пространстве

с учетом КНД приемной антенны;

• множитель ослабления;

• основное уравнение радиолинии (первое уравнение передачи)

Поле излучателя, находящегося в свободном пространстве

Свободное пространство представляет собой однородную безграничную непоглощающую среду, относительная диэлектрическая и магнитная прони­цаемости которой равны единице. Реально таких сред не существует, однако выражения, описывающие условия распространения радиоволн в этом случае, являются фундаментальными. Распространение радиоволн в более сложных случаях характеризуется такими же выражениями с внесением в них множителей, учитывающих влияние конкретных условий распространения.

Предположим, что в свободном пространстве помещен изотропный излу­чатель — воображаемый точечный излучатель, равномерно излучающий радио­волны во всех направлениях.

Плотность потока мощности (модуль вектора Пойнтинга) на расстоянии r от источника равна

где — излучаемая источником мощность, которая равномерно распределя­ется по поверхности сферы радиуса r.

Поле излучателя, находящегося в свободном пространстве

Среднее за период численное значение вектора Пойнтинга выражается формулой

где индекс «д» означает действующее значение.

Напряженность электрического и магнитного полей связаны между собой соотношением

где знаменатель представляет собой волновое сопротивление свободного про­странства (≈377 Ом).

Подставляя второе выражение в первое, получаем

Поле излучателя, находящегося в свободном пространстве

Следовательно вектор Пойнтинга можно вычислить двумя способами:

Приравняв эти два выражения, определим

Реально изотропные излучатели не существуют, а используются антенны, обладающие направленным излучением. Степень направленности антенны ха­рактеризуется ее коэффициентом направленного действия (КНД) по отно­шению к изотропному излучателю.

Понятие коэффициента направленного действия (КНД)

На рисунке показаны диаграммы направленности направленной антенны (А) и изотропного излучателя (В). Если обе антенны излучают одинаковые мощно­сти , то ясно, что в пункте приема, кото­рый достаточно удален от антенны, и на ко­торый ориентирована направленная антен­на, большая напряженность поля создается от направленной антенны, так как она кон­центрирует излучаемую энергию в желае­мом направлении. Будем постепенно увели­чивать подводимую к изотропной антенне В мощность до тех пор, пока она не создаст такое же поле, что и направленная антенна А.

Множитель , показывающий, во сколько раз следует увеличить мощность, подводимую к изотропной антенне, чтобы она создавала такую же на­пряженность поля, что и направленная, носит название коэффициента на­правленного действия.

Поле излучателя, находящегося в свободном пространстве

с учетом КНД передающей антенны

Таким образом, направленная антенна по создаваемой ею в месте приема напряженности поля эквивалентна изотропной антенне, ко­торая излучает в раз большую мощность. Это позволяет представить фор­мулу для действующего значения напряженности поля, создаваемой в свобод­ном пространстве направленной антенной, в следующем виде

Амплитудное значение напряженности поля выражается формулой

Выражение для мгновенного значения напряженности электрического по­ля радиоволн можно записать в форме

Поле излучателя, находящегося в свободном пространстве

с учетом КНД передающей антенны

либо в символической записи

где — волновое число.

Чувствительность современных приемных устройств часто характеризуют значением мощности на входе, требуемой для уверенного приема сигналов. Для того, чтобы определить мощность, подводимую к входу приемного устройства, достаточно умножить плотность потока энергии в месте расположения прием­ной антенны на эффективную площадь этой антенны , которая определяется формулой

Поле излучателя, находящегося в свободном пространстве

с учетом КНД приемной антенны

где — коэффициент направленного действия приемной антенны.

В случае направленной антенны значение вектора Пойнтинга П₂ определяется с учетом КНД по следующему выражению:

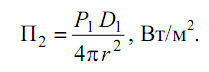
Умножая это значение на , получаем

Поле излучателя, находящегося в свободном пространстве

Отметим, что в диапазонах длинных, средних и ко­ротких волн иногда более удобно характеризовать передающую антенну с помощью силы, протекающего по ней тока. В основу расчета можно положить представление о находящемся в сво­бодном пространстве элементарном излучателе.

Обозначая через действую­щее значение силы тока и через — угол между осью излучателя и направле­нием на пункт приема, для напряженности поля на удалении , полу­чаем выражение:

где — действующая длина антенны.

Напряженность достигает максимума в экваториальной плоскости, ко­гда , при этом:

Множитель ослабления

Процесс распространения радиоволн над поверхностью Земли неразрывно связан с явлением поглощения энергии и со всякого рода потерями энергии. При распространении волн энергия теряется из-за проникновения радиоволн в толщу Земли, и вследствие поглощения в тропосфере и в ионосфере.

Ослабление поля радиоволны при распространении в реальных условиях по сравнению со значением этой величины, которое имело бы место при рас­пространении в свободном пространстве, принято характеризовать множите­лем или функцией ослабления . Если тем или иным способом определен множитель ослабления, то напряженность поля вычисляется но формуле

Мощность на входе приемника определится как

Множитель ослабления

Множитель ослабления радиоволн зависит от типа системы радиосвязи, диапазона частот, параметров Земли и атмосферы. Расчет множителя ослабления производится по формулам, приведенным либо в справочной литературе, либо в рекомендациях Международного Союза Электросвязи.

Например, величина множителя ослабления в случае, когда антенна расположена над плоской поверхностью (модель плоской Земли) в однородной изотропной среде, может быть рассчитана по следующей интерференционной формуле:

,

где R и θ – модуль и аргумент комплексного коэффициента отражения (зависит от поляризации поля, излучаемого антенной); – высота передающей антенны; – высота приемной антенны.

Основное уравнение радиолинии (первое уравнение передачи)

Основное уравнение радиолинии (первое уравнение передачи)

Мощность сигнала на входе приемника системы находится из, так называемого, основного уравнения радиолинии, которое имеет следующий вид:

,

где Р₁ – мощность передатчика; G₁ и G₂  коэффициенты усиления передающей и приемной антенн (, где  КНД антенны,  КПД антенны); ₁ и ₂  коэффициенты полезного действия фидера передающей и приемной антенн;   рабочая длина волны; r  длина линии радиосвязи; F  множитель ослабления.

Эта формула широко используется при анализе существующих и разработке новых систем радиосвязи.

Основное уравнение радиолинии (в логарифмическом виде)

Разделим обе части равенства на , возьмем от обеих частей и умножим на 10 каждое слагаемое полученного равенства. Тогда основное уравнение радиолинии в логарифмическом виде примет следующий вид:

или

.