ЭД / Новая папка (2) / DOC / ЛК 3 ТЭД_и_РРВ_ч_2

ЭД и РРВ (ЛК 3)

ОБЛАСТЬ ПРОСТРАНСТВА, СУЩЕСТВЕННАЯ ДЛЯ

РАСПРОСТРАНЕНИЯ РАДИОВОЛН.

ЗОНЫ ФРЕНЕЛЯ

• Область пространства, существенная для распространения радиоволн;

• принцип Гюйгенса;

• зоны Френеля;

• радиус зон Френеля;

• экспериментальное подтверждение существования зон Френеля;

• учет зон Френеля при проектировании радиолиний.

Область пространства, существенная для

распространения радиоволн

В большинстве практических задач распространения радиоволн расстояние между антеннами велико по сравнению с длиной волны. В этом случае для анализа распространения радиоволн широко используется метод геометрической оптики. В свободном пространстве согласно геометрической оптике электромагнитное поле распространяется по прямой, соединяющей точки передачи и приема.

Для выяснения границ применимости метода геометрической оптики и качественного анализа условий распространения радиоволн над земной  поверхностью оказывается полезным понятие области, существенной для распространения радиоволн.

  Областью пространства, существенной для распространения радиоволн, назовем область, в которой распространяется основная часть мощности от передающей к приемной антенне.

Принцип Гюйгенса

Пусть в точке А свободного пространства расположена передающая, а в точке В ― приемная антенна.

Определим область пространства, существенную для распространения радиоволн, формирующую сигнал в точке приёма. Размер и конфигурация такой области определяются принципом Гюйгенса  Френеля, согласно которому каждая точка фронта распространяющейся волны, созданной каким-то первичным источником А, сама является источником новой сферической волны. Полное поле в точке приема В может быть определено либо непосредственно как поле первичных источников, либо путем суммирования элементарных полей, создаваемых вторичными источниками, распределенными по замкнутой поверхности, охватывающей первичные источники. В теории такой вторичный источник называется элементарным источником Гюйгенса.

Зоны Френеля

Рассмотрим построение области пространства, существенной для распространения радиоволн, предложенное Френелем. Пусть в т. А помещён излучатель, а в т. В ― приёмная антенна.

Источник создаёт сферическую волну, т. е. волну, поверхностью равных фаз которой является сфера с центром в т. A. Построим конические поверхности с вершиной в т. В и осью АВ такие, чтобы образующие конусов отличались между собой на величину (n = 1, 2,…).

Зоны Френеля

Пересечение конусов с фронтом волны образует на сферической поверхности семейство коаксиальных окружностей. Участки поверхности сферы, заключённые между смежными окружностями, называются зонами Френеля. Первая, или главная, зона Френеля ― часть сферы, ограниченная окружностью N₁, зоны высших порядков представляют собой кольцевые области. При этом следует понимать, что образующие конусов отличаются между собой на величину , т.е. фазы радиоволн, излучаемых виртуальными источниками смежных зон, отличаются в среднем на .

Зоны Френеля

Из рисунка видно, что в поперечном сечении пространства между точками А и В зоны Френеля представляют собой семейство окружностей, а в продольном сечении семейство эллипсов с фокусами в точках А и В. Зная запись выражения уравнения эллипса и тот факт, что образующие конусов зон Френеля отличаются между собой на величину , можно записать следующее выражение

. (1)

Зоны Френеля могут быть построены на поверхности произвольной формы, например, на плоской поверхности S.

Радиус зон Френеля

Н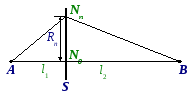айдём радиус n-й зоны Френеля на плоскости S, перпендикулярной

направлению распространения, в предположении, что распространяется плоская радиоволна. Согласно обозначениям на рисунке при условии, что l₁, l₂ >> , из прямоугольных треугольников АN_nN₀ и ВN_nN₀ можно записать следующие выражения:

, .

Подставив данные выражения в уравнение (1), после несложных преобразований получим выражение для определения радиуса зон Френеля следующего вида: .

Экспериментальное подтверждение существования зон Френеля

Экспериментально существование зон Френеля подтверждается, например, изменчивостью в точке приёма B напряжённости поля, создаваемого источником в т. A, при изменении радиуса R отверстия в условно бесконечном экране. В полном соответствии с принципом Гюйгенса сложение сигналов от не перекрытых еще зон Френеля приводит к колебаниям сигнала.

На рисунке приведен график зависимости отношения напряженности поля Е в точке наблюдения  к полю свободного пространства Е₀ от числа зон Френеля n = S/S₁, помещающихся в отверстии радиуса R.

Учет зон Френеля при проектировании радиолиний

Р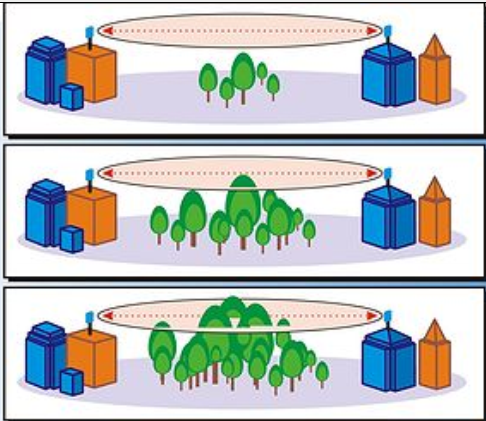адиоволна в процессе распространения в пространстве занимает объем в виде эллипсоида вращения с максимальным радиусом в середине пролета, который называют зоной Френеля. Естественные (земля, холмы, деревья) и искусственные (здания, столбы) преграды, попадающие в это пространство ослабляют сигнал.

Обычно блокирование 20% 1-й зоны Френеля вносит незначительное затухание в канал. Блокирование свыше 40% 1-й зоны Френеля вносит значительное затухание сигнала, этот факт указывает на то, что для сохранения работоспособности радиолинии следует избегать попадания препятствий в 1-ю зону Френеля.

Учет зон Френеля при проектировании радиолиний

Таким образом, при проектировании радиолиний рассматривают до 6 ― 8 зон Френеля, что позволяет обеспечить чистоту первой зоны Френеля с учетом изменения пространства между передающей и приемной антенной в длительный период времени. Высоту подвеса антенн следует определять с учетом величины радиуса 6 ― 8 зоны Френеля (высота подвеса антенн ).