
- •157 Техническая электродинамика
- •Введение
- •Раздел 1 теоретические основы электродинамики
- •1.1. Источники электромагнитного поля
- •1.2. Векторы электромагнитного поля
- •1.3. Материальные уравнения. Классификация сред
- •1.4. Уравнения Максвелла в дифференциальной и интегральной
- •1.5. Граничные условия для векторов электромагнитного поля
- •1.6. Метод комплексных амплитуд
- •1.7. Уравнения Максвелла для комплексных векторов
- •1.8. Комплексная диэлектрическая и магнитная
- •1.9. Энергия электромагнитного поля
- •Раздел 2 распространение электромагнитных волн в свободном пространстве
- •2.1. Решение уравнений Максвелла для комплексных амплитуд
- •2.2. Плоские электромагнитные волны в среде без потерь
- •2.3. Плоские электромагнитные волны в среде с тепловыми потерями
- •2.4. Поляризация электромагнитных волн
- •2.5. Распространение волн в анизотропных средах
- •Раздел 3 электромагнитные волны в направляющих системах
- •3.1. Типы направляющих систем
- •3.2. Классификация направляемых волн
- •3.3. Особенности распространения волн в направляющих системах
- •3.4. Волны в прямоугольном волноводе
- •3.5. Волны в круглом волноводе
- •3.6. Волны в коаксиальном кабеле
- •3.7. Волны в двухпроводной и полосковой линиях
- •3.8. Диэлектрический волновод. Световод
- •3.9 Направляющие системы с медленными волнами
- •3.10. Затухание волн в направляющих системах
- •Раздел 4 излучение электромагнитных волн
- •4.1. Понятие элементарного электрического излучателя
- •4.2. Поле элементарного электрического излучателя в дальней зоне
- •4.3. Мощность и сопротивление излучения элементарного электрического излучателя
- •4.4. Диаграмма направленности элементарного электрического излучателя
- •4.5. Перестановочная двойственность уравнений Максвелла
- •4.6. Элементарный магнитный излучатель и его поле излучения
- •4.7. Принцип эквивалентности. Принцип Гюйгенса
- •4.8. Принцип взаимности
- •4.9. Параметры антенн
- •4.10. Симметричный электрический вибратор
- •4.11. Директорные антенны
- •4.12. Зеркальные антенны
- •Раздел 5 распространение электромагнитных волн
- •5.1. Законы Снеллиуса. Коэффициенты Френеля
- •5.2. Явление полного прохождения волны через границу двух сред
- •5.3. Явление полного отражения от плоской границы раздела
- •5.4. Структура электромагнитного поля при полном
- •5.5. Поле вблизи поверхности хорошего проводника. Приближенные
- •5.6. Дифракция электромагнитных волн
- •5.7. Параметры Земли. Учет рельефа земной поверхности
- •5.8. Параметры тропосферы. Влияние тропосферы на распространение радиоволн. Тропосферная рефракция
- •5.9. Строение ионосферы. Понятие критической и максимально
- •5.10. Классификация радиоволн по способам распространения
- •5.11. Классификация радиоволн по диапазонам
- •5.12. Расчет действующего значения напряженности поля. Понятие
- •5.13. Особенности распространения радиоволн различных диапазонов
- •Литература
- •Приложение а вывод уравнений максвелла в дифференциальной форме
- •Приложение в вывод граничных условий для векторов электромагнитного поля
- •Приложение с волноводные устройства
- •Режимы работы линий передачи конечной длины. Согласование линии с нагрузкой
- •Приложение е математический аппарат электродинамики
Раздел 1 теоретические основы электродинамики
1.1. Источники электромагнитного поля
Принято считать, что источниками электромагнитного поля являются электрические заряды и токи. Рассмотрим кратко эти понятия.
Величина электрического заряда имеет размерность Кулон (Кл) и обозначается буквами q либо Q. Электрический заряд – одно из свойств элементарных частиц. Различают два вида зарядов: положительные и отрицательные. Электрические заряды обуславливают силовые взаимодействия между заряженными телами и частицами. Если одна из заряженных частиц меняет свое местоположение, сила ее воздействия на другие частицы меняется лишь спустя некоторый промежуток времени, пропорциональный расстоянию между частицами: воздействие одного заряженного тела передается на другое с конечной скоростью. Для объяснения такого рода явлений вводится новый физический объект – электромагнитное поле. Таким образом, взаимодействие между заряженными частицами осуществляется через электромагнитной поле.
Электромагнитное поле определяется как особый вид материи, характеризующийся способностью распространяться в вакууме со скоростью, близкой к 300 Мм/с, и оказывающий силовое воздействие на заряженные частицы.
Электромагнитное поле представляет собой единство двух своих составляющих – электрического и магнитного полей. Считают, что макроскопическое электромагнитное поле определено, если в каждой точке пространства известны величины и направления четырех векторов:
![]() –напряженности
электрического поля;
–напряженности
электрического поля;
![]() –электрического
смещения (электрической индукции);
–электрического
смещения (электрической индукции);
![]() –магнитной
индукции;
–магнитной
индукции;
![]() –напряженности
магнитного поля.
–напряженности
магнитного поля.
Пусть в некотором произвольном объеме V заключен заряд величиной q. В рамках макроскопической электродинамики для каждой точки M этого объема можно ввести понятие объемной плотности заряда с помощью следующей формулы:
![]() ,
,
![]() ,
,
где
q
– величина заряда, сосредоточенного в
объеме V
окрестности точки M
с радиус-вектором
![]() .
.
Очевидно,
что для равномерно распределенного
заряда
![]() .
.
Пусть на поверхности S распределен заряд величиной q. Тогда для каждой точки этой поверхности можно ввести понятие поверхностной плотности заряда s с помощью следующей формулы:
![]() ,
,
![]() ,
,
где q – величина заряда, распределенного на поверхности S в окрестности точки M.
Для
равномерного распределения заряда
![]() .
.
Зная плотности заряда, можно найти величину заряда в объеме или на поверхности с помощью следующих объемного или поверхностного интегралов:
![]() ,
,
![]() .
(1.1)
.
(1.1)
Заряды
могут быть покоящиеся и движущиеся.
Если объемный заряд движется со скоростью
![]() ,
то в каждой точке поля можно определитьвектор
объемной плотности тока проводимости
,
то в каждой точке поля можно определитьвектор
объемной плотности тока проводимости
![]() ,
,
равный
по величине пределу отношения заряда
![]() ,
проходящего за время
,
проходящего за время![]() через площадку
через площадку![]() ,
перпендикулярную направлению движения
зарядов, к произведению
,
перпендикулярную направлению движения
зарядов, к произведению![]() при
при![]() и
и![]() :
:
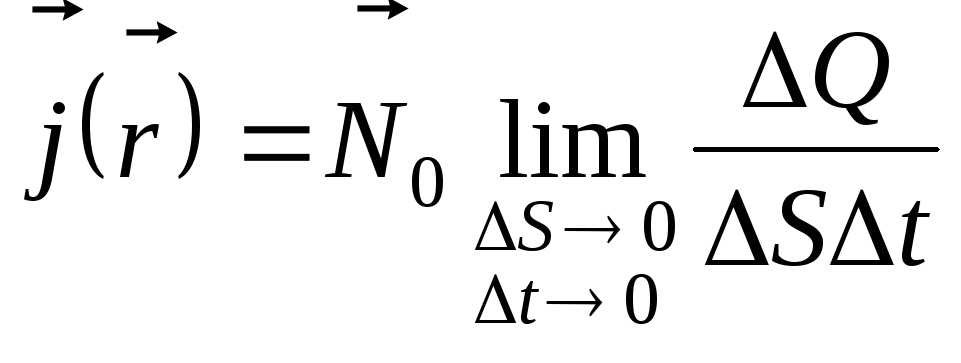 ,
,
где
![]() – орт, направление которого совпадает
с направлением движения зарядов.
– орт, направление которого совпадает
с направлением движения зарядов.
Нетрудно видеть, что вектор объемной плотности тока проводимости имеет размерность А/м2.
Пусть
в каждой точке некоторой поверхности
S
вектор
![]() известен. Тогда величина тока, протекающего
через всю поверхность S,
может быть найдена по следующей формуле:
известен. Тогда величина тока, протекающего
через всю поверхность S,
может быть найдена по следующей формуле:
![]() ,
(1.2)
,
(1.2)
где
вектор
![]() называют векторным дифференциалом
поверхности, а вектор
называют векторным дифференциалом
поверхности, а вектор![]() определяет орт нормали к поверхностиS.
определяет орт нормали к поверхностиS.
Аналогично
вводится понятие
вектора поверхностной плотности тока
проводимости.
Вектор поверхностной плотности тока
проводимости обозначается через
![]() и имеет размерность А/м.
и имеет размерность А/м.
Отметим, что поверхностные плотности (заряда и тока) могут быть сосредоточены только на поверхности идеального проводника.
