
- •157 Техническая электродинамика
- •Введение
- •Раздел 1 теоретические основы электродинамики
- •1.1. Источники электромагнитного поля
- •1.2. Векторы электромагнитного поля
- •1.3. Материальные уравнения. Классификация сред
- •1.4. Уравнения Максвелла в дифференциальной и интегральной
- •1.5. Граничные условия для векторов электромагнитного поля
- •1.6. Метод комплексных амплитуд
- •1.7. Уравнения Максвелла для комплексных векторов
- •1.8. Комплексная диэлектрическая и магнитная
- •1.9. Энергия электромагнитного поля
- •Раздел 2 распространение электромагнитных волн в свободном пространстве
- •2.1. Решение уравнений Максвелла для комплексных амплитуд
- •2.2. Плоские электромагнитные волны в среде без потерь
- •2.3. Плоские электромагнитные волны в среде с тепловыми потерями
- •2.4. Поляризация электромагнитных волн
- •2.5. Распространение волн в анизотропных средах
- •Раздел 3 электромагнитные волны в направляющих системах
- •3.1. Типы направляющих систем
- •3.2. Классификация направляемых волн
- •3.3. Особенности распространения волн в направляющих системах
- •3.4. Волны в прямоугольном волноводе
- •3.5. Волны в круглом волноводе
- •3.6. Волны в коаксиальном кабеле
- •3.7. Волны в двухпроводной и полосковой линиях
- •3.8. Диэлектрический волновод. Световод
- •3.9 Направляющие системы с медленными волнами
- •3.10. Затухание волн в направляющих системах
- •Раздел 4 излучение электромагнитных волн
- •4.1. Понятие элементарного электрического излучателя
- •4.2. Поле элементарного электрического излучателя в дальней зоне
- •4.3. Мощность и сопротивление излучения элементарного электрического излучателя
- •4.4. Диаграмма направленности элементарного электрического излучателя
- •4.5. Перестановочная двойственность уравнений Максвелла
- •4.6. Элементарный магнитный излучатель и его поле излучения
- •4.7. Принцип эквивалентности. Принцип Гюйгенса
- •4.8. Принцип взаимности
- •4.9. Параметры антенн
- •4.10. Симметричный электрический вибратор
- •4.11. Директорные антенны
- •4.12. Зеркальные антенны
- •Раздел 5 распространение электромагнитных волн
- •5.1. Законы Снеллиуса. Коэффициенты Френеля
- •5.2. Явление полного прохождения волны через границу двух сред
- •5.3. Явление полного отражения от плоской границы раздела
- •5.4. Структура электромагнитного поля при полном
- •5.5. Поле вблизи поверхности хорошего проводника. Приближенные
- •5.6. Дифракция электромагнитных волн
- •5.7. Параметры Земли. Учет рельефа земной поверхности
- •5.8. Параметры тропосферы. Влияние тропосферы на распространение радиоволн. Тропосферная рефракция
- •5.9. Строение ионосферы. Понятие критической и максимально
- •5.10. Классификация радиоволн по способам распространения
- •5.11. Классификация радиоволн по диапазонам
- •5.12. Расчет действующего значения напряженности поля. Понятие
- •5.13. Особенности распространения радиоволн различных диапазонов
- •Литература
- •Приложение а вывод уравнений максвелла в дифференциальной форме
- •Приложение в вывод граничных условий для векторов электромагнитного поля
- •Приложение с волноводные устройства
- •Режимы работы линий передачи конечной длины. Согласование линии с нагрузкой
- •Приложение е математический аппарат электродинамики
2.3. Плоские электромагнитные волны в среде с тепловыми потерями
Рассмотрим
случай когда в среде имеются только
тепловые потери, т.е. когда
0,
![]() ,
а
,
а![]() .
.
В этом случае комплексные амплитуды векторов плоской волны описываются формулами (2.1) и (2.2). Найдем для рассматриваемого случая комплексное волновое число и комплексное волновое сопротивление среды. Для дальнейшего удобно комплексное волновое число представить в алгебраической, а комплексное волновое сопротивление в показательной форме.
Используя формулы (2.4), получаем:
![]() , (2.14)
, (2.14)
![]() , (2.15)
, (2.15)
где
![]() ,
(2.16)
,
(2.16)
![]() , (2.17)
, (2.17)
![]() . (2.18)
. (2.18)
Величина , определяемая формулой (2.16), называется коэффициентом фазы или постоянной распространения волны, а величина – коэффициентом затухания волны. Из формулы (2.15) следует, что комплексное волновое сопротивление среды имеет индуктивный характер.
Перейдем во временную область, т.е. найдем действительные векторы монохроматического поля, соответствующие комплексным амплитудам (2.1) и (2.2). Используя формулы (2.14), (2.15) и (2.18), получаем следующие выражения:
![]() , (2.19)
, (2.19)
 .
(2.20)
.
(2.20)
Выражения (2.19) и (2.20) описывают плоскую электромагнитную волну в свободном пространстве с тепловыми потерями. Анализ этих формул проводиться так же, как и формул (2.7) и (2.8). Из сравнения формул (2.19) и (2.20) с аналогичными для среды без потерь следует:
– роль волнового числа в среде с потерями играет величина – постоянная распространения волны или коэффициент фазы;
– в
среде с потерями векторы
![]() и
и![]() имеют
сдвиг фаз, равный
имеют
сдвиг фаз, равный![]() ;
;
– амплитуды векторов по мере движения волны убывают по экспоненте с коэффициентом затухания .
Приведем без вывода некоторые свойства и основные параметры плоской волны в среде с потерями.
Длина волны:
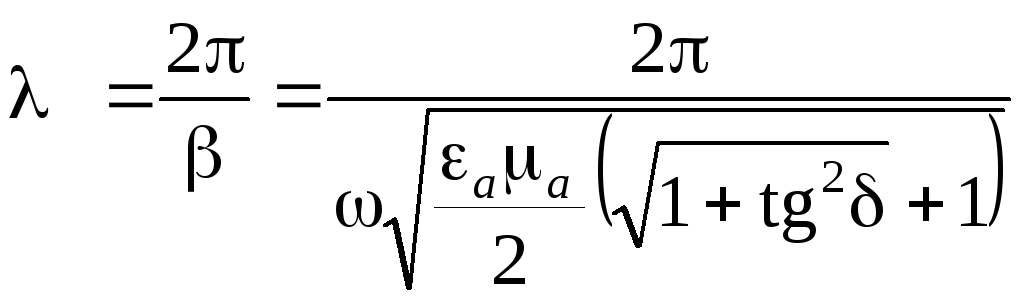 . (2.21)
. (2.21)
Фазовая скорость:
 . (2.22)
. (2.22)
Из
формулы (2.22) следует, что в среде с
потерями фазовая скорость зависит от
частоты
![]() .
Это явление называютдисперсией
волн, а среды, в которых фазовая скорость
плоской волны зависит от частоты,
называются диспергирующими.
Наличие дисперсии приводит к искажению
сигналов, так как при передаче сигналов
различные составляющие спектра сигнала
распространяются с разными скоростями.
Это приводит к изменению спектра сигнала,
а значит к искажениям во временной
области.
.
Это явление называютдисперсией
волн, а среды, в которых фазовая скорость
плоской волны зависит от частоты,
называются диспергирующими.
Наличие дисперсии приводит к искажению
сигналов, так как при передаче сигналов
различные составляющие спектра сигнала
распространяются с разными скоростями.
Это приводит к изменению спектра сигнала,
а значит к искажениям во временной
области.
Сравнивая формулы (2.21) и (2.22), видим, что
![]() ,
,
где Т – перид.
Последнюю формулу часто принимают за определение длины волны. Именно, длина волны равна расстоянию, которое проходит волна (фронт волны) за перид.
Отметим
следующее. При рассмотрении электромагнитных
волн, распространяющихся в однородных
средах длину волны принято обозначать
через
![]() ,
как это сделано в этом и предыдущем
разделах. При рассмотрении электромагнитных
волн в направляющих системах, вблизи
границы раздела двух сред используется
обозначение
,
как это сделано в этом и предыдущем
разделах. При рассмотрении электромагнитных
волн в направляющих системах, вблизи
границы раздела двух сред используется
обозначение![]() .
Величину, равную отношению скорости
света в вакууме к частоте генератора,
называютдлиной
волны
генератора
и обозначают через
.
Величину, равную отношению скорости
света в вакууме к частоте генератора,
называютдлиной
волны
генератора
и обозначают через
![]() .
.
3.
Сдвиг фаз
![]() между векторами
между векторами![]() и
и![]() приводит к появлению мнимой части в
комплексном векторе Пойнтинга:
приводит к появлению мнимой части в
комплексном векторе Пойнтинга:
![]() .
.
Действительная часть, т.е. средняя за период плотность потока энергии, равна
![]() .
.
Отметим, что реактивная составляющая вектора Пойнтинга соответствует колеблющемуся потоку энергии, периодически (четыре раза за период) изменяющему направление своего движения.
4. Для характеристики скорости распространения сигнала в среде с потерями вводят понятие групповой скорости. Под групповой скоростью (vгр) понимают скорость распространения огибающей спектра двух гармонических волн с близкими частотами. Групповая скорость также зависит от частоты и может быть рассчитана по следующей формуле:
![]() . (2.23)
. (2.23)
5.
Глубина проникновения поля в
среду
определяется как расстояние, при
прохождении которого амплитуды векторов
убывают в
![]() раз и обозначается через0.
При этом
раз и обозначается через0.
При этом
![]() .
.
Ниже приведены некоторые формулы для двух частных случаев.
Среда близкая к диэлектрической или слабо диспергирующая среда (tg << 1):
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;![]() .
.
Среда близкая к проводящей или сильно диспергирующая среда (tg >> 1):
![]() ,
,
![]() ,
,
![]() ;
; ![]() ,
,![]() .
.
