Додаток А. Деякі відомості з математики

А1. Елементи векторної алгебри

В геометрії вектором (в вузькому сенсі) зветься будь-який направлений відрізок, який має початок та кінець. Кінець вектора позначається стрілкою.

Модулем вектора зветься його довжина (звичайні позначки чи ).

Два ненульових вектора вважаються рівними, коли вони мають однакову довжину (модуль) та однаковий напрям (повністю співпадають при паралельному переносі - дивись рис. 1, на якому , , ). Всі нульові вектори вважаються рівними. У всіх інших випадках вектори не рівні. Кутом між векторами є кут між їх напрямами.

Вираз „проекція вектора на вісь” має два тлумачення:

а) Геометрична проекція вектора на вісь – вектор, початок якого є проекція початку вектора на вісь, а кінець – проекція кінця вектора на вісь (наприклад, та на рис. 2). Модуль вектора може бути визначено за його проекціями в прямокутній системі координат

= .

б) Алгебраїчна проекція вектора на вісь – число, яке дорівнює різниці координат кінця і початку вектора (наприклад, для вектора , рис. 2, маємо: > 0, < 0).

Складання векторів (операція однозначна) – сумою векторів і зветься вектор , який побудовано за будь-яким з наступних правил:

- Правило трикутника – вектор переноситься паралельно самому собі таким чином, щоб його початок був розташований в кінці вектора . Сумою векторів буде вектор , який проведено з початку вектора в кінець вектора (дивись рис. 3).

- Правило паралелограма - вектор переноситься паралельно самому себе таким чином, щоб його початок був розташований в початку вектора . Сумою векторів буде вектор - діагональ паралелограма, яка проведена з початку вектора у протилежний кут паралелограма побудованого на сторонах і (дивись рис. 4).

Якщо відомі проекції векторів (, , ) і (, , ), то

= + , = + , = + .

Добуток вектора і скаляра

Добутком вектора на скалярну величину є вектор , який в ‌‌‌ разів довший, ніж вектор . Цей вектор спрямований у той же бік, що і вектор , якщо додатна і в протилежний, якщо від’ємна.

Скалярний добуток векторів

Скалярний добуток векторів ( і ) – це число , яке визначається за наступними правилами: = = , де – кут між векторами і . Скалярний добуток дорівнює нулю, якщо модуль одного чи обох векторів дорівнює нулю, або коли вектори взаємно перпендикулярні.

Якщо відомі проекції векторів (, , ) та (, , ),то в декартовій системі координат

= · +· + ·.

Зауважимо, що · = ·.

Векторний добуток векторів

Векторний добуток векторів і – це вектор , модуль якого визначається як , де – кут між векторами і . Результуючий вектор розташовано перпендикулярно до векторів і , а його напрям визначається за правилом правого свердлика: якщо обертати перший вектор так, щоб найкоротшим поворотом сумістити його з другим, то поступальний рух свердлика вкаже напрям добутку векторів. Векторний добуток дорівнює нулю, якщо модуль одного чи обох векторів дорівнює нулю, чи вектори паралельні.

Якщо відомі проекції векторів (, , ) і (, , ) в декартовій системі координат, то

.

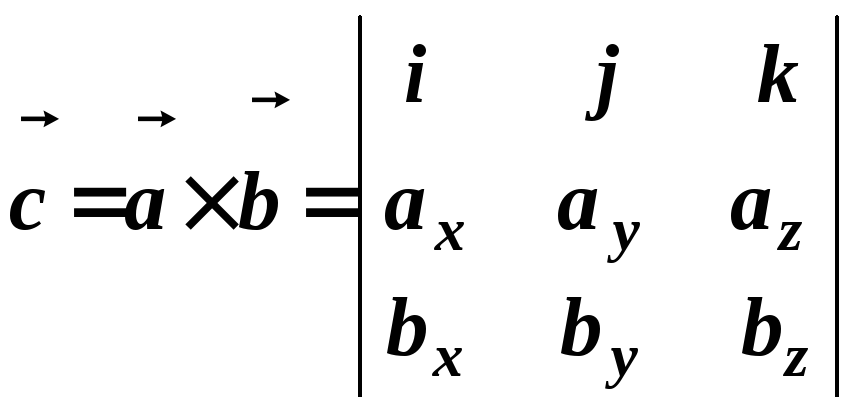Тут , , - орти декартової системи координат. Тоді:

,

,

.

Зауважимо, що .

А2. Властивості трикутників

Для будь-якого трикутника (рис. 4) виконується:

а) Теорема синусів: .

б) Теорема косинусів:

,

,

.

А3. Елементи аналітичної геометрії

Рівняння прямої, що проходить через точку ( та –декартові координати точки), під кутом до осі

,

тут .

Відстань від довільної точки до цієї прямої

.

Рівняння кола радіуса з центром у точці

.

Рівняння еліпса з півосями і з центром у точці

.

А4. Основи диференціального числення

Таблиця елементарних похідних ().

Функція	Похідна		Функція	Похідна
	0
				–

Основні правила заходження похідних:

1) Похідна суми:

2) Похідна добутку:

3) Похідна дробу:

4) Похідна складної функції:

А5. Таблиця елементарних інтегралів

А6. Властивості визначених інтегралів

,

,

.

Тут - первісна підінтегральної функції .

Додаток Б. Моменти інерції однорідних тіл

Диск у площині
Прямокутник у площині
Куля
Тонкий стрижень		= 0

Додаток В. Правила оформлення

розрахунково-графічних робіт (РГР)

В ряді ВНЗ (згідно з навчальним планом дисципліни) студенти виконують та захищають розрахунково-графічні роботи (РГР).

Перелік задач, що входять до РГР, та їх кількість визначається навчальною програмою дисципліни.

При виконанні РГР та її оформленні слід дотримуватися наступних правил:

1. Робота виконується на стандартних аркушах паперу формату А4 та оформляється лише з однієї сторони аркуша.

2. Титульний аркуш містить:

• назву навчального закладу;

• назву факультету;

• назву кафедри, на якій виконується робота;

• назву розрахунково-графічної роботи;

• номер варіанту;

• назви задач, які входять до даної РГР;

• прізвище та ім’я студента (курсанта);

• прізвище та ініціали викладача, який приймає РГР;

• рік виконання роботи.

Зразок титульного аркуша наведений на наступній сторінці.

3. На другій сторінці наводяться повні і скорочені умови задачі.

4. На наступних сторінках наводяться схеми механізмів (конструкцій) і послідовно (зверху вниз) записується хід розв’язання завдання з коментарями, відповідними перетвореннями та розрахунками.

5. Якщо треба розв’язати задачу графічно, то графічний розв’язок виконується на окремому аркуші міліметрівки. При цьому вказуються масштаби величин, які потрібно визначити та результати вимірювань.

6. Рисунки та графіки виконуються з дотримуванням вимог креслення або у графічному редакторі, яким студент (курсант) володіє.

7. Розрахунки проводяться з точністю до 3-4-х значущих цифр. У відповіді вказуються отримані результати та одиниці їх вимірювання.

Якщо робота не відповідає наведеним вимогам, вона не допускається до захисту і вважається такою, що не виконана.

На захисті кожної задачі з РГР студент (курсант) повинен довести, що в достатньої мірі засвоїв матеріал та отримав навики розв’язання задачі.

Одеська національна морська академія

Факультет морського судноводіння

Кафедра теоретичної механіки

Розрахунково-графічна робота

з теоретичної механіки

Задачі:

1. Визначення реакцій опор плоскої конструкції

2. Визначення центра ваги просторових однорідних тіл

3. Знаходження швидкостей та прискорень точок тіла, яке здійснює плоский рух

4. Знаходження абсолютної швидкості та абсолютного прискорення точки, яка здійснює складний рух

Варіант № 10

Виконав курсант

Козаченко Дмитро

група 1117

Робота захищена

(оцінка)

доцент Петренко О. І.

Одеса 2013

Література

Основна

1. Павловський М. А. Теоретична механіка: Підручник. – Київ: Техніка, 2002. – 512 с.: іл.

2. Макарова Т. В. Курс теоретичної механіки: Кінематика. Статика: Навчальний посібник. – Одеса: Астропринт, 2003. – 232 с.

3. Цасюк В. В. Теоретична механіка: Навчальний посібник. –Київ: Центр навчальної літератури, 2004. – 402 с.

4. Козицький С. В., Латиш О. М., Швець О. І. Теоретична механіка. Задачі і приклади їх розв’язування. Навчальний посібник з грифом МОНУ. Видання друге, виправлене. – Одеса: ОНМА, 2009. – 260 с.

5. Козицький С. В. Теоретична механіка: Стислий курс. Навчальний посібник. – Одеса: ОНМА, 2004. – 122 с.

6. Козицький С. В. Стислий курс теоретичної механіки: (частина 2). Динаміка системи матеріальних точок та твердого тіла. Навчальний посібник. – Одеса: ОНМА, 2005. – 116 с.

Додаткова

1. Тарг С. М. Краткий курс теоретической механики. Учебник для втузов – М.: Высш. шк., 2007. – 416 с.: ил.

2. Сборник заданий для курсовых работ по теоретической механике: Учеб. пособие для техн. вузов; Под ред. А. А. Яблонского. – 4-е изд. М.: Высшая школа, 1985. – 367 с.

3. Бать М.И., Джапаридзе Г. Ю, Кельзон А.С., Теоретическая механика в примерах и задачах. – М.: Наука, 1984. т.1. – 602 с; – М.: Наука, 1985. т.2. – 558 с.

4. Козицький С. В., Поліщук Д. І. Механіка. Підручник . - Одеса: Астропринт, 2011. – 472 с.

5. Выгодский М.Я. Справочник по высшей математике – М.: Наука, 1977. – 871 с.

112