Для сукупності паралельних осей обертання момент інерції твердого тіла має мінімальне значення для осі, яка проходить через центр маси твердого тіла. Тоді для будь-якої іншої осі, паралельної до неї, момент інерції можна визначити за теоремою Гюйгенса-Штейнера

, (3.11)

де – маса тіла, а – відстань між осями (рис. 3.2).

Моменти інерції більшості однорідних тіл правильної форми відносно їх центру мас можна знайти у довідниках з фізики чи математики.

Похідна за часом від вектора моменту кількості руху механічної системи відносно даного центра дорівнює головному моментузовнішніх сил відносно того ж центра

. (3.12)

Формула (3.12) є математичним записом теореми про зміну моменту кількості руху механічної системи у диференціальній формі і називається такожосновним рівнянням обертального руху.

Векторне рівняння в проекціях на нерухомі вісі декартової системи координат еквівалентне трьом скалярним рівнянням

,,. (3.13)

З рівняння (3.12) отримуємо

. (3.14)

Після інтегрування (3.14) в межах від початкового моменту часу до поточного, отримуємо

, (3.15)

де – момент кількості руху механічної системи на поточний час, а– в момент часу. Таким чином,зміна моменту кількості руху механічної системи відносно нерухомого центру за проміжок часу віддодорівнює інтегралу від головного моменту зовнішніх сил по часу за той самий проміжок часу.

Формула (3.15) є математичним записом теореми про зміну моменту кількості руху механічної системи у інтегральній формі.

З наведеної теореми випливають наступні наслідки:

1) внутрішні сили безпосередньо не впливають на зміну моменту кількості руху механічної системи (вони можуть здійснювати опосередкований вплив через зовнішні сили);

2) якщо головний момент зовнішніх сил відносно деякого нерухомого центру дорівнює нулю, то момент кількості руху механічної системивідносно того ж центра не змінюється. Дійсно, якщо, то з рівняння (3.12) матимемо

=, (3.16)

де – початкове значення вектора. Формула (3.14) є першим інтегралом рівняння руху системи і математичним записом закону збереження моменту кількості руху механічної системи;

3) якщо головний момент всіх зовнішніх сил не дорівнює нулю, але його момент відносно деякої вісі (наприклад, ) дорівнює нулю, то момент кількості руху механічної системи відносно цієї вісі не змінюється з часом. Дійсно з рівняння (3.15) випливає, що коли, наприклад,, то

, (3.17)

тобто зберігається відповідна проекція моменту кількості руху механічної системи.

Зауважимо, що формули (3.12) та (3.15) отримані на підставі закону Ньютона, які виконуються в інерціальній системі відліку. У випадку складного руху окремих частин системи потрібний імпульс в рівнянні (3.7) визначається як сума імпульсів відносного та переносного рухів

. (3.18)

Контрольні запитання

1. Що характеризує момент кількості руху матеріальної точки?

2. Як знайти момент кількості руху матеріальної точки?

3. В яких випадках момент кількості руху матеріальної точки дорівнює нулю?

4. Як знайти момент кількості руху механічної системи?

5. Як знайти момент кількості руху твердого тіла відносно заданої осі?

6. Що таке момент інерції твердого тіла? Що він характеризує? В яких одиницях вимірюється?

7. Як формулюється теорема Гюйгенса-Штейнера?

8. Чи можуть внутрішні сили змінити момент кількості руху механічної системи? Чому?

9. Сформулюйте теорему про зміну моменту кількості руху механічної системи у диференціальній та інтегральній формах.

10. Сформулюйте теорему про збереження моменту кількості руху механічної системи.

11. Сформулюйте теорему про збереження проекції моменту кількості руху механічної системи.

Методика розв’язання задач

Розглянемо два типи задач, коли на тілі (платформі), що обертається, розташовані тіла, які вважаємо матеріальними точками:

Тип 1) розташування тіл у механічній системі не змінюється при дії на неї моменту зовнішніх сил:

1. Суміщаємо вісь з віссю обертання платформи.

2. Знаходимо проекції моменту кількості руху механічної системи для початкового та кінцевого станів, коли тіла нерухомі відносно платформи

, (1)

, (2)

де – момент інерції платформи відносно осі(якщо вісь не проходить через центр маси, то потрібно скористатися теоремою Гюйгенса-Штейнера),,–початкова та кінцева кутові швидкості платформи,та– маси та віддалі тіл (які вважаємо матеріальними точками) від осі().

2. Обчислюємо зміну моменту кількості руху за рахунок моменту зовнішніх сил протягом заданого часу

. (3)

3. На підставі теореми про зміну моменту кількості руху записуємо рівняння

, (4)

з якого знаходимо кінцеву кутову швидкість системи.

Тип 2) на систему не діє момент зовнішніх тіл, але в системі відбувається рух тіл, які входять у систему:

1. Суміщаємо вісь з віссю обертання платформи.

2. Знаходимо проекцію моменту кількості руху механічної системи для початкового стану, коли тіла нерухомі відносно платформи

, (4)

де – момент інерції платформи відносно осі,– початкова кутова швидкість,та– маси та віддалі тіл (які вважаємо матеріальними точками) від осі().

3. Знаходимо момент кількості руху механічної системи для моменту часу , коли точки системи рухаються відносно платформи. В цьому випадку швидкість кожної точки системи знаходимо за формулою складання швидкостей складного руху, тобто

. (5)

Тому для моменту кількості руху рухомої матеріальної точки записуємо

+.

Вважаючи, що напрям обертання не змінюється, для кінцевого значення проекції моменту кількості руху механічної системи отримуємо

, (6)

де – віддаль від осі обертання до лінії, вздовж якої напрямлений вектор переносної швидкості;– віддаль від осі обертання до лінії, вздовж якої напрямлений вектор відносної швидкості. При цьому знак «+» в дужках ставимо у випадку, коли напрями векторних добутківтаспівпадають, а знак «–» - коли ці напрями протилежні.

Оскільки для переносної швидкості точки , де– відстань точки від осі обертання для моменту часу, тоді з рівняння (6) отримуємо

. (7)

4. Прирівнюючи вирази (4) та (7) отримаємо рівняння

,

звідки знаходимо кінцеву кутову швидкість обертання .

Приклад 1.Однорідний диск маса якого= 400 кг і радіус= 5 м обертається навколо вертикальної фіксованої осі, яка проходить через його центр перпендикулярно до його площини з початковою кутовою швидкістю= 4 рад/с (рис. 3.3). На відстанім від осі обертання в стані спокою знаходиться механізм масою= 150 кг. В момент часу= 0 на систему починає діяти момент зовнішніх сил. Визначити кутову швидкістьобертання диска в момент часу= 2 с.

Далі диск обертається за інерцією з досягнутим значенням кутової швидкості. В деякий новий момент часу самохідний механізм переміщується в нове положення на відстань= 2 м від центру диску та зупиняється. Вважаючи механізм матеріальною точкою, знайти кутову швидкість диску на цей момент, нехтуючи тертям у підшипниках.

Розв’язання. Розглянемо рух механічної системи, сумістивши вісьсистеми відліку з віссю обертання диску. Скористаємося теоремою про зміну проекції моменту кількості руху механічної системи у інтегральній формі

,

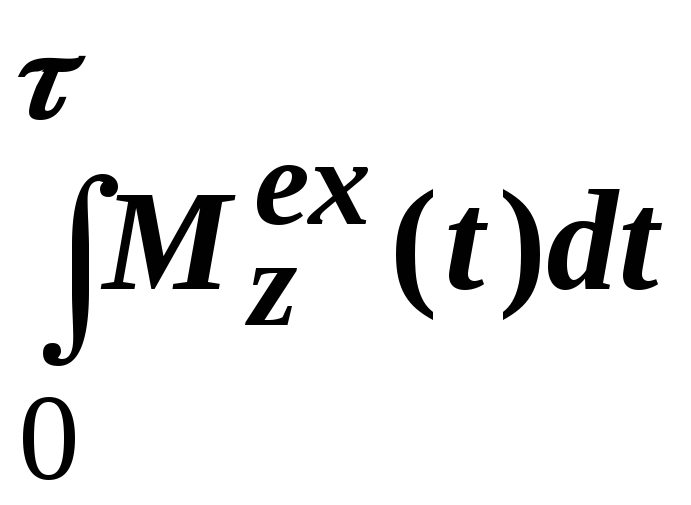де –- проекція моменту кількості руху системи, який складається з диска та механізму;- головний момент зовнішніх сил, прикладений до системи, відносно осі.

Сили, які діють на систему - це сили тяжіння та, реакції підп’ятниката підшипникаі момент зовнішніх сил. Сили тяжіння спрямовані паралельно осі обертання і, відповідно, їхні моменти відносно цієї осі дорівнюють нулю. Не створюють моменту і сили реакції, бо вони перетинають вісь. Отже, головний момент зовнішніх сил дорівнює моменту=.

Момент кількості руху системи є сумою моментів імпульсів її елементів. Момент кількості руху диску, який має момент інерції відносно осіта обертається навколо неї з кутовою швидкістювизначається за формулою

,

в якій - момент інерції диску відносно осі обертання.

Для матеріальної точки, згідно з визначенням (3.1) запишемо проекцію її моменту кількості руху на вісь як

,

де - радіус-вектор, який проведено від осі обертання до точки, а- абсолютна швидкість точки. Якщо точка не рухається відносно диску (), то абсолютна швидкістьточки, дорівнює її переносній швидкості, яка визначається за формулою Ейлера

,

отже

.

Таким чином проекція моменту кількості руху системи на вісь може бути записана у вигляді

,

а рівняння зміни моменту кількості руху під дією зовнішнього моменту сил приймає вигляд

.

Звідки отримуємо

.

Підставляючи чисельні значення, знаходимо

рад/c.

Після того, як перестав діяти момент зовнішніх сил , диск обертається у відсутності сил тертя за інерцією. Така ситуація дає можливість скористатись теоремою про збереження проекції моменту кількості руху на цю вісь

,

де та- відповідно- проекції початкового і кінцевого моменту кількості руху системи. Прирівнюючи отримані вирази для моменту кількості руху системи у початковий та кінцевий моменти часу маємо

=,

що дозволяє отримати вираз для розрахунку кінцевої кутової швидкості обертання диску

.

Підставляючи чисельні значення, знаходимо

рад/c.

Відповідь:= 4,6 рад/с.

Приклад 2.Однорідний диск маса якого= 300 кг і радіус= 8 м обертається навколо вертикальної фіксованої осі, яка проходить через його центр перпендикулярно до його площини з кутовою швидкістю= 5 рад/с. На відстані= 7 м від центру диску в стані спокою знаходиться механізм масою= 100 кг. В момент часу= 0 механізм починає рухатись вздовж кола незмінного радіусаза закономв напрямі обертання диску (відстань в метрах, час в секундах). Вважаючи механізм матеріальною точкою, знайти кутову швидкість диску як функцію часута її значення на момент часу= 2 с.

Розв’язання.Сумістимо вісьсистеми відліку з віссю обертання диску та позначимо сили, які діють на систему - це сили тяжіння диската механізму, реакції підп’ятниката підшипника(рис. 3.4). Ці сили не створюють моментів відносно осі, тому скористуємось теоремою про збереження проекції моменту кількості руху на цю вісь

,

де тапочаткова і кінцева- проекції моменту кількості руху системи відповідно. Вираз для початкової проекції моменту кількості руху знайдено у попередньому прикладі

.

Коли механізм почне рухатися, абсолютна швидкість точки складається зі швидкості відносного тапереносного рухів, яку має будь-яка точка диску завдяки обертанню диска, тому для моменту кількості руху точки маємо

,

де - радіус-вектор, який проведено від осі обертання до точки. Швидкість переносного руху точки у довільний момент часу

,

модуль відносної швидкості визначимо як першу похідну відносного переміщення точки за часом

,

і спрямована вона по дотичній до траєкторії відносного руху.

Беручи до уваги напрям руху точки та, вважаючи, що напрям обертання диску не змінився, для абсолютної швидкості точки отримаємо

.

Записуємо кінцеве значення - проекції моменту кількості руху точки

,

і остаточно для кінцевого значення - проекціїмоменту кількості руху системи знайдемо

,

де - кінцева кутова швидкість обертання диску.

Тоді з умови збереження - проекції моменту кількості руху механічної системи отримуємо вираз для знаходження кінцевої кутової швидкості диску

.

Підставимо дані задачі та обчислимо значення для кінцевої кутової швидкості диску на момент часу = 2 с

= 4,03 рад/с.

Відповідь:= 4,03 рад/с.

Самостійнопроаналізуйте задачу, для випадку коли відносна швидкість механізму протилежна переносній швидкості точок диска.

Приклад 3. Квадратна однорідна платформа маса якої= 300 кг і розмір= 3 м обертається навколо вертикальної фіксованої осі, що проходить через центр платформи перпендикулярно до її площини з кутовою швидкістю=5рад/с (рис. 3.5). Механізм масою=50кг знаходиться в точців стані спокою. В момент часу= 0 починає діяти момент зовнішніх сил(Н^.м) і діє протягом часу. Визначити кутову швидкістьобертання тіла та її значення при=4с.

Після цього дія зовнішнього моменту припиняється і в новий момент часу = 0 механізм починає рухатись вздовж прямоїза законом(відстань в метрах, час в секундах). Вважаючи механізм матеріальною точкою, знайти кутову швидкість платформи на момент часуТ = 1 с.

Розв’язання. Сумістимо вісьсистеми відліку з віссю обертання платформи та позначимо сили, які діють на систему - це сили тяжіння диската механізму, реакції підп’ятниката підшипниката момент зовнішніх сил(рис. 3.6). Головний момент зовнішніх сил визначається тільки моментом, оскільки усі вказані сили не створюють моментів відносно осі.

Запишемо теорему про зміну - проекції моменту кількості руху механічної системи

, (1)

де та- початкова і кінцева- проекції моменти кількості руху системи відповідно.

Знайдемо вираз для моменту кількості руху механічної системи у довільний момент часу. Він складається з моментів імпульсів платформи та нерухомого відносно платформи механізму, отже отримуємо , (2)

де - момент інерції плат форми відносно заданої осі обертання.

Оскільки в початковий момент механізм нерухомий, то його абсолютна швидкість дорівнює переносній

,

тому отримуємо

. (3)

Підставляючи дані задачі послідовно знаходимо

_z= 300∙(3²+ 3²)/3 = 1800 кг∙м²,

= 50∙2∙3²∙= 900∙кг∙м²/c,

.

Після цього обчислюємо інтеграл.

кг∙м²/c.

Підставляючи отримані результати у формулу (1), отримуємо

,

звідки знаходимо значення кутової швидкості у заданий момент часу з врахуванням умов задачі

рад/с.

Після цього моменту, згідно з умовами задачі, дія моменту зовнішніх сил припиняється і далі обертання платформи здійснюється у відсутності сил тертя. Це дає можливість скористатися теоремою про збереження проекції моменту кількості руху на вісь z

, (4)

де –- проекція моменту кількості руху у довільний момент часу.

Вираз для згідно (3) має вигляд

=. (5)

Коли механізм рухається, його абсолютна швидкість дорівнює, тому вираз для- проекції моменту кількості руху системи у довільний момент часу прийме вигляд

(6)

де – кутова швидкість обертання платформи,та- віддалі від точкидо ліній, вздовж яких напрямлені швидкості переносного рухута відносного руху, відповідно.

Для обчислення виразу (6) в момент часу Т = 1 с. визначаємо:

1) положення механізму на траєкторії відносного руху

м.

Оскільки (м), то механізм знаходиться в точці(рис. 3.7), тобто

2) швидкість переносного руху механізму ;

3) величину . Для цього визначаємо кут(см. рис. 3.5) з геометричних міркувань:= 0,447, тоді= 3·0,447 = 1,34 (м)

4) швидкість відносного руху = 6,71 (м/с).

Таким чином, вираз для кінцевого значення - проекції моменту кількості руху, з урахуванням напрямів векторівта, запишемо в вигляді

. (7)

Прирівнюючи вирази в (4) (5) та (7) отримуємо рівняння для визначення кутової швидкості

,

звідки знаходимо

= 1,4 рад/с.

Відповідь:= 1 рад/с,=1,4 рад/с.

Приклад 4. Тіло утворено стрижнем довжиною= 0,5 м та масою= 37 кг, до кінця якого приєднано однорідний диск масою= 290 кг, радіус якого0,8 м. (рис. 3.8). Тіло обертається з кутовою швидкістю = 2 рад/с навколо вертикальної фіксованої осі, яка перпендикулярна до площини, в який лежить стрижень та диск. Механізм масою= 10 кг знаходиться в точців стані спокою. В момент часу= 0 починає діяти момент зовнішніх сил(Н^.м) і діє протягом часу. Нехтуючи силами тертя у підшипнику та підп’ятнику, визначити кутову швидкість обертання тіла при=4с.

Після цього в новий момент часу = 0 тіло продовжує обертання за інерцією, а механізм починає рухатись вздовж дугиза законом(відстань в метрах, час в секундах). Вважаючи механізм матеріальною точкою, знайти кутову швидкість диску на момент часуТ= 1 с.

Розв’язання. Сумістимо вісьсистеми відліку з віссю обертання платформи. Запишемо теорему про зміну- проекції моменту кількості руху механічної системи

, (1)

де та- початковий і кінцевий моменти кількості руху системи відповідно,- головний момент зовнішніх сил, прикладений до системи, відносно осі.

Вкажемо зовнішні сили, які діють на систему - це сили тяжіння диска, стрижнята механізму, реакції підшипниката підп’ятниката пара сил з моментом(рис. 3.9). Головний момент зовнішніх сил визначається тільки моментом, оскільки усі вказані сили не створюють моментів відносно осі.

Знайдемо вираз для моменту кількості руху механічної системи у довільний момент часу. Він складається з моментів імпульсів стрижня, диска та механізму, отже отримуємо

, (2)

де

м.

Момент інерції стрижня та диска відносно осі zзнаходимо скориставшись теоремою Гюйгенса - Штейнера

кг·м².

Оскільки протягом часу дії зовнішнього моменту сили механізм не рухається відносно диску, знаходячись у точціА (рис. 3.10), то його абсолютна швидкість дорівнює переносній

,

модуль якої дорівнює

.

Тому отримуємо вираз для моменту кількості руху системи на будь-який момент часу

. (3)

Після цього згідно з (1) обчислюємо визначений інтеграл.

кг·м²/с.

Підставляючи отримані результати у формулу (1), отримуємо вираз, який дозволяє знайти кутову швидкість обертання тіла у довільний момент часу

,

і знаходимо значення кутової швидкості у заданий момент часу

рад/с.

Після цього моменту, згідно з умовами задачі, дія моменту зовнішніх сил припиняється і далі обертання платформи здійснюється у відсутності сил тертя. Це дає можливість скористатися теоремою про збереження моменту кількості руху відносно осі

, (4)

де –проекція моменту кількості руху у момент часу,

–проекція моменту кількості руху у момент часу Т= 1 с.

знаходимо з формули (3)

кг·м²/с.

Коли механізм рухається, його абсолютна швидкість дорівнює , тому вираз для- проекції моменту кількості руху системи у довільний момент часу прийме вигляд

, (5)

де – кутова швидкість обертання платформи,та- відстані від точкидо ліній, вздовж яких напрямлені швидкості переносного рухута відносного руху, відповідно.

Для розв’язання другої частини задачі визначаємо:

1) положення механізму на траєкторії відносного руху в заданий момент часу

м,

,

та позначаємо його точкою А₁(рис. 3. 11).

2) швидкість відносного руху ,

м/с,

яка спрямована по дотичній до траєкторії відносного руху (рис. 3.11),

3) відстань від осі обертання (точки на рис. 3.11) до лінії, вздовж якої напрямлена швидкість відносного руху

= 0,5 м.

4) відстань механізму від осі обертання переносника =DA₁з трикутникаDA₁О

= 1,39 м.

5) швидкість переносного руху механізму

.

Таким чином, вираз (5) для кінцевого значення проекції моменту кількості руху, з урахуванням напрямів векторів та, запишемо в вигляді

,

в якому кутова швидкість диску на момент часуТ та обчислимо його

.

Прирівнюючи вирази , отримуємо рівняння для визначення кутової швидкості

,

звідки знаходимо

рад/с.

Відповідь:== 6 рад/с,рад/с.