Закінчення таблиці СП.6

№	Судно (спостерігач)		Судно (ціль)
			= 0		= 0,1 год
	вузли	градуси	градуси	милі	градуси	милі
21	22	280	227	11,5	222	8,5
22	25	160	220	13	225	9,8
23	22	262	305	11,2	310	8,2
24	21	260	320	13,7	324	10,5
25	19	105	67	11,8	72	8,8
26	23	193	140	12,5	135	9,6
27	22	110	55	11,8	50	8,7
28	24	348	38	13,3	42	10,3
29	21	195	158	11,5	163	8,5
30	20	15	313	11,4	308	8,8

§ 5. Динаміка прямолінійного руху судна

При відсутності течії та вітру і прямому положенні руля судно здійснює горизонтальний прямолінійний рух, диференціальне рівняння якого, має вигляд

, (5.1)

де – маса води, яка „прихоплюється” зануреною частиною корпусу судна при його русі,– сила тяги двигуна. Оскільки обтікання судна при характерних експлуатаційних значеннях швидкості супроводжується виникненням турбулентного потоку, то сила опору водного середовища пропорціональна квадрату швидкості

, (5.2)

де - коефіцієнт опору водного середовища, який залежить від завантаження судна, форми зануреної частини корпусу та його стану, а знак „–” вказує, що ця сила напрямлена завжди проти швидкості руху судна (рис. 5.1.).

В модельних розрахунках величина приймається рівною 10% маси судна, тобто= 0,1m. Для спрощення формул, введемо– ефективну масу судна, тоді рівняння (5.1) з врахуванням (5.2) в проекції на вісь, яку спрямуємо за напрямом руху судна, приймає вигляд

. (5.3)

Рівняння (5.3) доповнюють початковими умовами: при = 0:= 0,.

Кожному значенню силу тяги > 0 відповідає перехідний процес зміни швидкості (), який закінчується досягненням усталеного значення швидкості

. (5.4)

В залежності від значення та напряму тяги маємо три різні ситуації:

– передній хід(тяга спрямована вздовж швидкості) – у цьому випадку в рівнянні (5.3) перед модулем тяги ставимо знак „+”;

– пасивне гальмування(рух за інерцією) –= 0;

– активне гальмування(реверсний режим роботи двигуна – тяга спрямована проти вектора швидкості) – у цьому випадку в рівнянні (5.3) перед модулем тяги ставимо знак „–”.

В рівнянні (5.3) можна розділити змінні

, (5.5)

та провести інтегрування з невизначеною верхньою межею

. (5.6)

З останнього отримуємо

, (5.7)

що дозволяє знаходити час як функцію швидкості , або (після відповідних алгебраїчних перетворень) визначати швидкість судна як функцію часу. Зауважимо, що результат інтегрування (5.7) залежить від конкретного вигляду підінтегральної функції.

Для визначення шляху, який проходить судно, можна скористатися інтегруванням , але простіше скористуватися перетворенням

. (5.8)

Тоді з рівняння (5.3) отримуємо

, (5.9)

що, за умовами (= 0:= 0,), дозволяє визначити шлях, який проходить судно в процесі зміни швидкості від початковоїдо поточного значення

=, (5.10)

і таким чином визначити шлях як складну функцію часу .

Розглянемо кожну з ситуацій (> 0,= 0 та< 0) окремо, а при можливій зміні режиму роботи двигуна будемо нехтувати перехідними процесами. Тобто будемо працювати в рамках моделі, коли сила тяги (упору) гвинта при зміні числа обертів змінюється миттєво від початкового значення = constдо кінцевого значення= const.

Методика розв’язання задач

1. Визначити сили, які діють на судно в горизонтальному напрямі.

2. Спрямувати вісь у напрямі руху судна та спроектувати сили на цю вісь.

3. Записати диференціальне рівняння руху судна.

4. Для визначення швидкості як функції часу:

а. Розділити змінні, взяти інтеграли з невизначеною верхньою межею

та отримати зв’язок між поточною швидкістю та часом.

б. Провести алгебраїчні перетворення та отримати вираз .

5. Для визначення переміщення як функції часу:

а. Переписати диференціальне рівняння руху судна, користуючись

перетворенням (7.8).

б. Розділити змінні, взяти інтеграли з невизначеною верхньою межею

та отримати зв’язок між переміщенням та швидкістю.

Приклад 1. Передній хід судна.Судно масою= 15000 т рухається вперед під дією сили тяги= 11 кН зі сталою швидкістю. Коефіцієнт опору води= 11000 кг/м.

В момент часу = 0 оберти двигуна змінено так, щоб він забезпечував постійне значення тяги= 420 кН у напрямі руху і судно протягом часузбільшує швидкість до величини= 11 вузлів.

1) Знайти час , протягом якого відбулася зміна швидкості та шлях, який при цьому пройде судно. Величину шляху перевести в морські одиниці (милі).

2) За допомогою ПЕОМ побудувати графіки залежності швидкості від часу та шляху від часу.

Розв’язання. В даному випадку сила тяги має той же напрям, що і швидкість судна (рис. 7.1), диференціальне рівняння руху судна (5.1) приймає вигляд

, (5.11)

а інтеграли (5.7) та (5.10) дають:

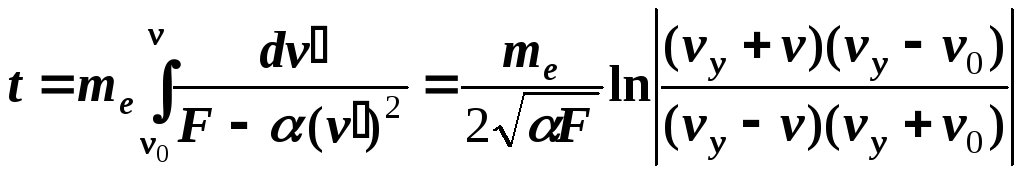, (5.12)

, (5.13)

де – усталена швидкість, яка відповідає початковому значеннюсили тяги, а– усталена швидкість для нової сили тяги.

Для того, щоб скористуватися формулами (5.12) та (5.13) переведемо дані задачі в одиниці системи SI:

= 11·(1852/3600) = 5,66 м/с,

визначимо ефективну масу

= 1,65·10⁷кг,

початкову швидкість судна

= 1 м/с,

та усталену швидкість судна для тяги = 420 кН

= 6,18 м/с.

Після цього обчислимо час , протягом якого відбувається зміна швидкості, та шлях , який при цьому проходить судно. Тоді з формул (5.12) та (5.13) отримуємо:

340 с6,0 хв.,

1349 (м) = 0,73 милі.

Щоб побудувати графіки залежності швидкості та шляху, потрібно у явному виді з рівняння (5.12) визначити залежність швидкості від часу

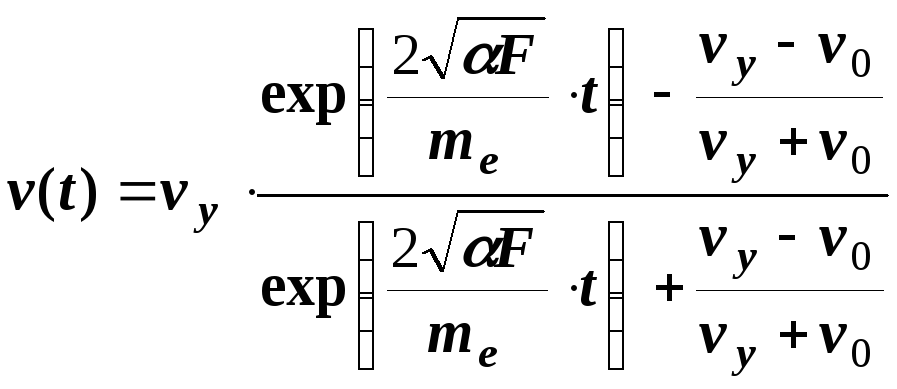, (5.14)

та за допомогою відомого програмного забезпечення (Basic, Pascal, Microsoft Excel чи ін.) знайти значення в продовж часу руху судна, а потім визначені значення швидкості для кожного моменту часу підставити у формулу (5.13) та обчислити значення. Отримані графікитазображені на рис. 5.2 та 5.3.

Відповідь: = 6 хв.,= 0,73 милі.

Приклад 2. Тепер розглянемо два можливі варіанти гальмування судна після досягнення швидкості 11 вузлів до швидкості 2,5 вузли – випадки пасивного і активного гальмування судна.

а) Пасивне гальмування судна(= 0). При швидкості= 11 вузлів двигун вимикають, судно рухається по інерції і зменшує швидкість до= 2,5 вузлів. Знайти часгальмування судна та шлях, який пройшло судно за цей час. Шлях виразити в морських одиницях (милях).

Розв’язання. В цьому випадку гальмування судна відбувається за рахунок лише сили опору з боку води (див. рис. 5.4), тому рівняння (5.1) приймає вигляд

, (5.15)

а інтеграли (5.7) та (5.10) дають:

, (5.16)

, (5.17)

де - швидкість судна на початку гальмування (= 11 вузлів = 5,66 м/с), а– швидкість судна на відповідний момент часу= 2,5 вузли = 1,29 м/с.

Підставляючи дані у формули (5.16) та (5.17), обчислимо час гальмування та шлях, якій пройшло судно за цей час:

= 900 (с) = 15 хв.,

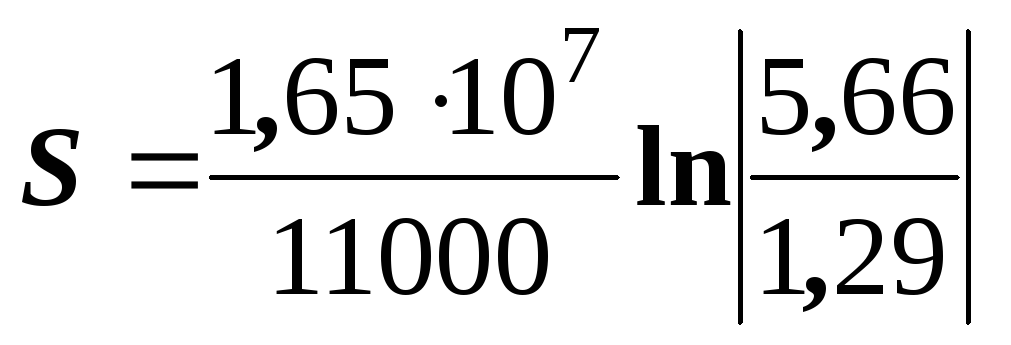= 2221 (м) = 1,2 милі.

Для побудови графіків залежності швидкості та шляху, потрібно провести алгебраїчні перетворення у формулі (5.16) та визначити швидкість як функцію часу (зробить це самостійно) і побудувати графіки аналогічно тому, як це робилось у попередньому прикладі.

Для розібраного прикладу графікитанаведені на рисунках 5.5 та 5.6.

Відповідь: = 900 с,= 1,2 милі.

б) Активне гальмування судна (< 0). При швидкості= 11 вузлів двигун переводять у режим реверсу (= 125 кН, векторспрямований проти вектора швидкості судна, рис. 5.7).

1) Знайти час , протягом якого швидкість судна зменшиться до значення= 2,5 вузла та визначити шлях, який пройдено за цей час.

2) За допомогою ПЕОМ побудувати графіки залежності швидкості від часу та шляху від часу.

Протягом часу судно зменшує швидкість до.

Розв’язання. В цьому випадку гальмування судна відбувається як за рахунок сили опору з боку води, так і за рахунок сили тяги двигуна. Тому диференціальне рівняння руху судна приймає вигляд (тяга спрямована проти руху – рис. 5.7)

, (5.18)

а інтеграли (5.7) та (5.10) дають:

, (5.19)

, (5.20)

де - швидкість судна на початку гальмування ( = 11 вузлів = 5,66 м/с).

Підставимо наші дані в формули (5.19) та (5.20) і отримаємо:

= 445[1,034 – 0,365] = 298 с = 5 хв.,

= 906 (м) = 0,49 милі.

Для побудови графіків залежності швидкості та шляхупотрібно у явному виді з рівняння (5.19) знайти залежність швидкості від часу

, (5.21)

та за допомогою відомого програмного забезпечення (Basic, Pascal, Microsoft Excel чи ін.) обчислити значенняв продовж часу руху судна, а потім визначені значення швидкості для кожного моменту часу підставити у формулу (4.20) та знайти значення. Отримані графікитазображені на рис. 5.8 та 5.9.

Зверніть увагу на те, що при активному гальмуванні судна (при заданому значенні) для зниження швидкості від 11 вузлів до 2,5 потрібно втричі менш часу ніж при пасивному гальмуванні, а судно проходить відстань в 2,4 разу меншу.

Відповідь: = 5 хв.,= 0,49 милі.