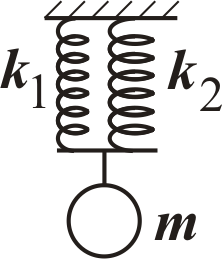Контрольні запитання

1. Сформулюйте умови виникнення змушених коливань.

2. Запишіть диференціальне рівняння змушених коливань. Що необхідно знати для однозначного розв’язку такого рівняння?

3. Запишіть розв’язок диференціального рівняння змушених коливань.

4. Чим визначаються період змушених коливань?

5. Як впливають початкові умови на амплітуду і фазу змушених коливань?

6. Як впливає сила тертя на амплітуду і фазу змушених коливання?

7. За яким законом змінюється амплітуда змушених коливань? Від яких факторів залежить амплітуда змушених коливань?

8. Намалюйте графік залежності амплітуди змушених коливань від частоти збурювальної сили (амплітудно-частотну характеристику змушених коливань) для різних значень сили тертя (коефіцієнта згасання).

9. Намалюйте графік амплітудно-фазової характеристики змушених коливань (графік залежності зсуву фаз між змушеними коливаннями та зовнішньої силою від частоти сили) для різних значень сили тертя (коефіцієнта згасання).

10. Який випадок змушених коливань називається резонансом?

Приклад. Тіло масою= 0,5 кг знаходиться на похилій площині, яка утворює кут 60° з горизонтом (рис. 5.6), воно прикріплено до двох пружин жорсткістю= 60 Н/м та = 140 Н/м на і здійснює коливання під дією збурювальної силипри наявності сили опоруН.

1) Записати диференціальне рівняння змушених коливань, знайти значення резонансної частоти, статичне зміщення та амплітуду змушених коливань при резонансі.

2) Побудувати амплітудно-резонансну криву в безрозмірних частотах в інтервалі (0; 2,0) для відносної (безрозмірної) амплітуди.

Розв’язання. Як і раніше, перш за все, знайдемо ефективний коефіцієнт жорсткості двох пружин. В даному прикладі пружини закріплені послідовно, але, на відміну від попереднього прикладу, стискування однієї пружини силоюсупроводжується розтягом другої пружини з такою ж силою, тому = 200 Н/м.

Запишемо диференціальне рівняння вимушених коливань с урахуванням сил тертя

,

та визначимо сталі, які входять до цього рівняння:

= 20 рад/с,

= 0,8/(2·0,5) = 0,8 рад/с,

= 14/0,5 = 28 м/с².

Всі ці величини є необхідними для подальших розрахунків. Так, резонансну частоту коливань визначимо за формулою (5.30)

== 19,9 рад/с,

амплітуду коливань в резонансі обчислимо, користуючись (5.31)

= 0,88 м,

а статичне зміщення – за формулою (5.29)

= 28/400 = 0,07 м.

Ця залежність наведена на рис. 5.7.

Для побудови амплітудно-резонансних кривих в безрозмірних частотах скористуємось виразом (5.32)

..

За допомогою ПЕОМ обчислюємо значення, та будуємо відповідний графік (рис. 5.8).

Відповідь:= 19,9 рад/с,= 0,07 м,= 0,88 м.

Задача ДТ.5. Дослідження одномірних вільних, згасаючих та змушених коливань

Тіло масою закріплено до двох недеформованих пружин жорсткістюі (рис. 1 - 6).

1) Знайти положення рівноваги, відносно якого мають місце коливання.

2) Записати диференціальне рівняння вільних незгасаючих коливань, скласти характеристичне рівняння та розв’язати його для заданих початкових умов ,. Визначити початкову фазу, частоту, та амплітудутаких коливань. Побудувати графік коливань протягом трьох періодів.

3) Записати диференціальне рівняння згасаючих коливань при наявності сили опору , та розв’язати його для тих самих початкових умов. Визначити початкову фазу, частоту, початкову амплітудуі декремент згасання. Користуючись ПЕОМ побудувати графік згасаючих коливань протягом трьох періодів та визначити з графіка декремент згасання.

4) Записати диференціальне рівняння змушених коливань для зовнішньої сили з урахуванням сили опору. Записати загальний розв’язок цього рівняння. Записати вираз для амплітуди та фази змушених коливань. Визначити статичне зміщення, резонансну частоту і амплітуду коливань в резонансі.

5) Перейти до безрозмірної частоти та, користуючись ПЕОМ, побудувати амплітудно-резонансну кривув інтервалі.

Необхідні дані наведені в таблиці ДТ.5.

На рис. 1 та 4 точка закріплення діліть відстань між пружинами у відношенні обернено пропорційному їх жорсткостям.

Тіло здійснює коливання вздовж вертикалі (рис. 1 та 2) чи вздовж похилої площини (рис. 3 – 6).

1	2	3
4	5	6

Таблиця ДТ.5 – вихідні дані для задачі ДТ.5

№	Рис.	, Н/м	, Н/м	, кг	, м	, м/с	, кг/с	, Н
1	1	150	50	2	0,1	2	0,4	6
2	2	54	108	1	-0,3	6	0.24	4
3	5	75	150	2	0,3	-2,5	0,32	3
4	3	150	255	5	-0,2	3,5	1,6	7
5	6	192	96	1	0,5	-4	0,32	2
6	1	260	124	6	-0,1	-6	1,8	9
7	2	147	294	2	-0,3	4	0,48	5
8	4	100	145	5	0,1	3	1,2	10
9	3	160	128	8	-0,2	-9	1,8	12
10	1	50	175	1	0,2	3	1,4	10
11	4	224	424	8	-0,3	-2	2,4	16
12	5	90	360	2	0,2	-7	0.44	4
13	6	640	160	2	-0,3	2	0,6	5
14	3	200	100	3	-0,3	4,5	1,12	9
15	2	243	486	2	0,4	7	0,64	4
16	4	224	224	7	-0,2	-3	2	14
17	6	250	250	5	0,3	-4	0,2	3
18	5	125	500	1	-0,5	8	0,7	15
19	1	290	260	5,5	0,3	4	2,4	6
20	6	216	108	2	-0,4	-6,5	0,4	5

Закінчення таблиці ДТ.5.

№	Рис.	, Н/м	, Н/м	, кг	, м	, м/с	, кг/с	, Н
21	3	108	108	6	0,1	-6	1,2	13
22	2	294	588	4	-0,4	3,5	1	7
23	5	80	320	1	0,3	-5,5	0,28	4
24	4	75	150	9	0,2	7,5	1,6	12
25	6	500	125	4	-0,3	-2	0,72	8
26	1	200	248	7	0,2	4,5	2,2	14
27	5	160	640	2	-0,1	-5	0,64	6
28	2	125	500	1	0,2	-2,5	0,8	2
29	3	144	144	8	-0,3	8,5	1,6	16
30	6	360	90	2	0,2	-9,5	0,44	8

208