§.5. Механічні коливання а) Вільні незгасаючі коливання з одним ступенем свободи

Малі коливання, які здійснює матеріальна точка масою під дією лише квазіупружної силиназиваються вільними (власними) незгасаючими. Такі одномірні коливання, наприклад, вздовж осі, описуються диференціальним рівнянням

,

з початковими умовами: = 0:та, чи

= 0, (5.1)

де – кругова частота коливань,– коефіцієнт жорсткості пружини, а відлік осі починається в точці, яка відповідає положенню рівноваги.

Зауважимо, що дія сталої сили на точку, яка здійснює коливання, змінює лише положення рівноваги, тобто точку, відносно якої здійснюються коливання, але не змінює рівняння коливань. Тому дія на точку сталої сили не впливає на результат розв’язку рівняння.

Характеристичне рівняння для однорідного диференціального рівняння зі сталими коефіцієнтами (5.1) має вигляд

= 0. (5.2)

Корені цього рівняння чисто уявні (,), тому загальний розв’язок рівняння (5.1) набуває вигляду

,

в якому та– сталі інтегрування.

Це рівняння, за допомогою перетворень Ейлера зводиться до вигляду

, (5.3)

в якому сталі коефіцієнти тавизначаються з початкових умов як:

,.

Рівняння (5.3), в свою чергу, зводиться до однієї гармонічної функції

. (5.4)

Коливання, які здійснюються за законом (5.3) чи (5.4) називаються гармонічними, але закон (5.4) аналізувати значно легше, ніж (5.3). Величина вказує найбільше відхилення точки від положення рівноваги і називаєтьсяамплітудою коливань, величина­–фазою коливань, а –початковою фазоюколивань.

Сталі інтегрування тазнаходять з початкових умов:

, (5.5)

. (5.6)

Звернемо увагу, що при визначенні початкової фази

, (= 0; 1), (5.7)

і необхідно знайти значення при яких задовольняються початкові умови.

Контрольні запитання

1. Сформулюйте умови виникнення коливань.

2. Як спрямована сила, що викликає гармонічні коливання? Чи існують в природі такі сили? Наведіть приклади.

3. Запишіть диференціальне рівняння коливального руху. Що необхідно знати для однозначного розв’язку такого рівняння?

4. Як отримати розв’язок такого рівняння?

5. Запишіть розв’язок диференціального рівняння коливального руху. Що таке період та амплітуда коливань?

6. Від чого залежить період (частота) коливань та амплітуда коливань?

7. Як впливає стала сила, що діє на матеріальну точку, на її коливання?

Методика розв’язання задач

1. Визначити ефективний коефіцієнт жорсткості пружин.

2. Визначити положення рівноваги тіла.

3. Записати диференціальне рівняння руху та скласти відповідне характеристичне рівняння.

4. Розв’язати характеристичне рівняння та проаналізувати його корені.

5. Скористатися перетворенням Ейлера та визначити гармонічну функцію.

6. Знайти сталі інтегрування, користуючись початковими умовами.

Приклад.Тіло масою= 0,5 кг прикріплено до двох з’єднаних паралельно недеформованих пружинах жорсткістю=60 Н/м та =140Н/м (рис. 5.1) і знаходиться на похилій площині під кутом 45º до горизонту. Точка закріплення тіла ділить відстань між пружинами у відношенні обернено пропорційно жорсткостям пружин. Знайти: 1) положення рівноваги, відносно якого мають місце коливання; 2) записати диференціальне рівняння вільних незгасаючих коливань та розв’язати його для початкових умов =0,1 м, =– 2,0 м/с; 3) визначити частоту, початкову фазута амплітудутаких коливань. Побудувати графік коливань.

Розв’язання. Перш за все, знайдемо ефективний коефіцієнт жорсткості. При паралельному з’єднанні пружин (коли точка закріплення ділить відстань між пружинами у відношенні обернено пропорційно їх жорсткостям) величина деформації кожної пружини однакова, а сумарна сила розтягу двох пружин є сумою сил деформації кожної пружини

,

тому ефективна жорсткість системи дорівнює сумі жорсткостей пружин

= 200Н/м.

Проведемо вісь вздовж похилої площини з початком у точці закріплення тіла (рис. 5.1). Положення рівновагивизначимо з умови рівності сили пружностіі проекції сили тяжіння на похилу площину45º, тобто з рівняння

45º,

звідки отримаємо

=0,018 м = 1,8 см..

Відносно цього положення, яке в подальшому вважаємо початком відліку х – координати,. будуть здійснюватися коливання.

Запишемо диференціальне рівняння вільних незгасаючих коливань відносно нового положення рівноваги

, (1)

або

.

Кругова частота коливань визначається жорсткістю системи пружин та масою тіла, і в нашому прикладі

=20рад/с.

Розв’язок диференціального рівняння коливань запишемо в вигляді

=, (2)

що для швидкості точки дає

. (3)

Підставимо початкові умови в ці вирази та отримаємо рівняння для визначення амплітуди та початкової фази коливань:

,. (4)

Якщо піднести ці вирази до другого ступеня та скласти, то можна отримати вираз для амплітуди, а якщо поділити – то вираз для початкової фази:

== 0,14 м, (5)

= 0,1·20/(– 2,0) = –1.

З останнього рівняння отримаємо

(–1) = –рад. (6)

Підстановка знайдених значень = 0,14 і= –в (2) та (3) при= 0 не відповідає початковим умовамта. Тому, з урахуванням властивостей тангенса, треба додати до знайденого значення початкової фази- період тангенса. Тоді

= 2,356 рад.

Тепер початкові умови зараз задовольняються:

= 0,1 м = ,

= –2,0 м/с = = ,

і розв’язок рівняння вільних незгасаючих коливань остаточно приймає вигляд

м.

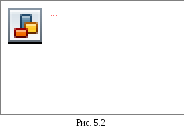
Графік коливань представлений на рис. 5.2.

Відповідь: =0,018 м,=20 рад/с, рад, = 0,14 м,м.