1	2
3	4
5	6
7	8
9	10
11	12
13	14
15	16

Таблиця К.2 – вихідні дані для задачі К.2

№ вар.	№ рис.	, рад/с3, (см/с3)	, рад/с2, (см/с2)	, с	, см	, см	, см	, см
1	1	1	-2	1	40	30	40	20
2	1	0	2	1	40	20	40	30
3	2	1	-4	2	45	-	30	20
4	2	0	1	2	50	-	40	20
5	3	1	-2	2	54	18	36	27
6	3	0	0,8	1	80	40	40	20
7	4	1	-3	2	45	15	30	15
8	4	0	2	0,5	45	15	25	20
9	5	-1	2	1	50	20	40	20
10	5	0	1,5	1	50	20	40	20
11	6	-1	3	2	40	20	30	20
12	6	0	1,4	1	40	20	30	20
13	7	1	-4	3	50	-	35	25
14	7	0	1,5	0,5	60	-	50	40
15	8	-1	2	2	15	-	50	10
16	8	0	0,6	0,2	25	-	80	25
17	9	1	-3	2	30	-	60	45
18	9	0	1,5	2	30	-	50	40
19	10	2	-1	1	20	-	40	25
20	10	0	1,5	0,5	20	-	40	25
21	11	1	-3	2	40	-	45	20
22	11	0	1	2,5	80	-	50	20
23	12	2	-3	1	20	-	50	40
24	12	0	1,5	0,4	20	-	50	40
25	13	1	-2	2	50	20	40	25
26	13	0	1	1	50	20	40	25
27	14	-1	0	1	10	-	50	40
28	14	0	1,6	1	10	-	50	25
29	15	0	2	2	25	25	40	30
30	16	0	2	2	50	-	50	40

§ 3. Плоский рух твердого тіла: а) визначення швидкостей точок

Плоским (чи плоскопаралельним) рухом називається такий рух твердого тіла, при якому всі точки тіла рухаються в незмінних площинах, паралельних до деякої нерухомої площини , яка носить назвуосновної. Отже, плоский рух твердого тіла можна звести до вивчення руху плоскої фігури, утвореної перетином тіла площиною(рис. 3.1). Тіло при плоскопаралельному русі має три ступені свободи. Цими трьома параметрами, як правило, є дві декартові координати (,) довільної точкиплоскої фігури (цю точку називаютьполюсом) і кут, який утворює відрізок, що лежить в площині фігури та з’єднує полюс і довільну точку, з віссю(рис. 3.1). При русі плоскої фігурив своїй площині величини, ізмінюються з часом:

,,. (3.1)

Перші два рівняння визначають поступальний рух полюса, а третє – рівняння обертання плоскої фігури навколо полюса.

Швидкість довільної точки фігури визначається з формули

+=+, (3.2)

де - поступальна швидкість полюса (точкиА),- швидкість точкив її обертальному русі разом з плоскою фігурою навколо цього полюса. Отже, швидкість довільної точки зображається діагоналлю паралелограма, побудованого в точціна векторахі(рис. 3.2).

Корисною для визначення швидкостей точок твердого тіла є теорема про проекції, яка формулюється наступним чином – проекції векторів швидкостей двох точок твердого тіла на лінію, яка їх з’єднує, алгебраїчні рівні (рис. 3.3)

, (3.3)

отже

. (3.4)

Зауважимо, що формули (3.3) та (3.4) справедливі при будь-якому русі твердого тіла.

При плоскому русі фігури, якщо її кутова швидкість не дорівнює нулю (≠ 0), в кожний момент часу існує єдина точка в цій площині, навколо якої фігура здійснює чисто обертальний рух. Ця точка називається миттєвим центром швидкостей (МЦШ)і, як правило, позначається буквою.Якщо ця точка належіть твердому тілу, то абсолютна швидкість цієї точки тіла в даний момент часу дорівнює нулю.

Якщо вибирати полюс у миттєвому центрі швидкостей , то модуль швидкості довільної точкиплоскої фігури визначається формулою

, (3.5)

ілінійна швидкість точкинаправлена перпендикулярно до прямої() за напрямом обертання фігури (рис. 3.4).

Отже, плоскопаралельний рух твердого тіла в кожний момент часу можна розглядати як безперервну послідовність нескінченно малих поворотів навколо миттєвого центру обертання. Зауважимо, що положення миттєвого центру швидкостей може змінюватись з плином часу.

Основні методи знаходження мцш

1. Якщо відомі лінії, вздовж яких спрямовані швидкості двох точок (рис. 3.4), то положення МЦШ знаходиться у точці перетину прямих, проведених через дві вибрані точки плоскої фігури перпендикулярно до лінії швидкості цих точок (рис. 3.4).

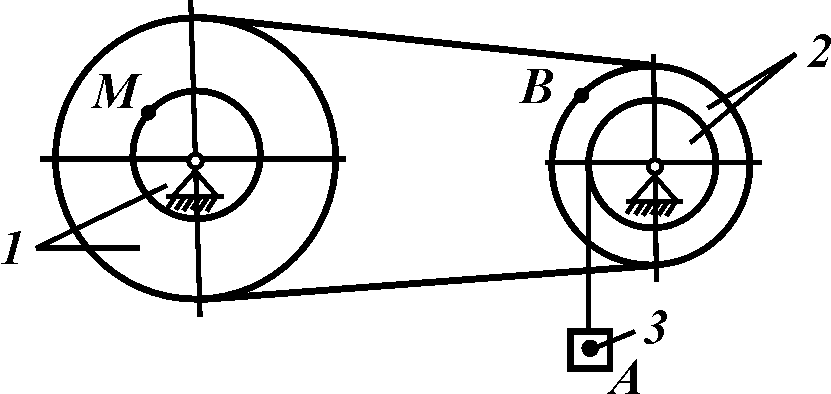
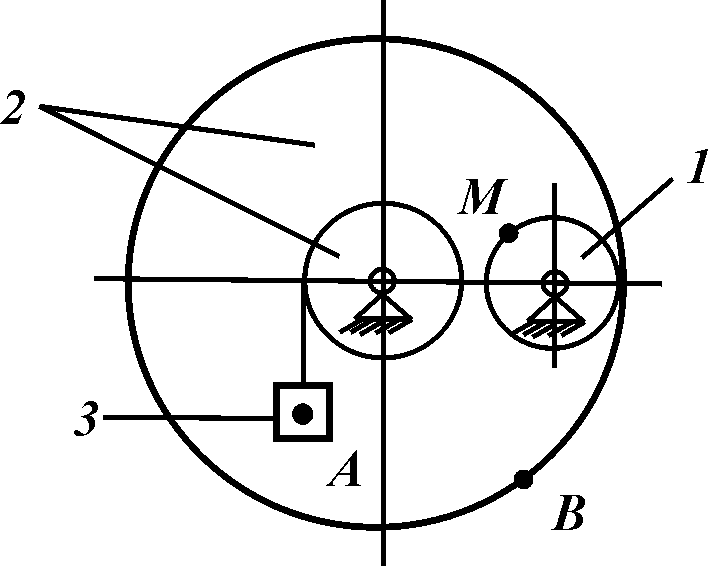
2. Якщо швидкості двох точок плоскої фігури спрямовані вздовж паралельних прямих і мають спільний перпендикуляр (рис. 3.5 а та рис. 3.5 б), то МЦШ знаходиться точці перетину перпендикуляра з лінією, проведеною через кінці векторів швидкостей (рис. 3.5 а та рис. 3.5 б). З подібності трикутників (дивись рис. 3.5 а і 3.5 б) отримаємо

. (3.6)

3. Якщо швидкості точокА іВ однакові (за модулем і напрямом) і перпендикуляр до них спільний (рис. 3.5 в), або швидкості точокАіСоднакові, але перпендикуляри до векторів різні (рис. 3.5 в) і вони не перетинаються, то точка перетину знаходиться у нескінченості. Тоді

,

а це означає, що в даний момент обертальна складова відсутня. Отже, фігура здійснює миттєво-поступальний рух, при якому швидкості усіх точок рівні

. (3.7)