§ 6. Фізичний маятник

Фізичний маятник – це будь-яке тіло, що підвішене у точці, яка не співпадає з центром його маси, та має можливість здійснювати коливання навколо цієї точки.

Розглянемо таке тіло, яке підвішене в точці та відхилене від положення рівноваги на кут (рис. 6.1). В цьому випадку сила тяжіння , яка прикладена до центру маси тіла (точка ), створює момент сили відносно точки підвішування

. (6.1)

Цей момент намагається повернути тіло навколо точки до положення рівноваги (у протилежну сторону від відхилення). Таким чином, основне рівняння обертального руху може бути записано у вигляді

, (6.2)

де – момент інерції тіла відносно точки підвішування.

Вираз (6.2) - нелінійне диференціальне рівняння, розв’язок якого є окремою математичною задачею. Проте для малих кутів відхилення рівняння (6.2) стає лінійним і зводиться до відомого рівняння гармонічних коливань

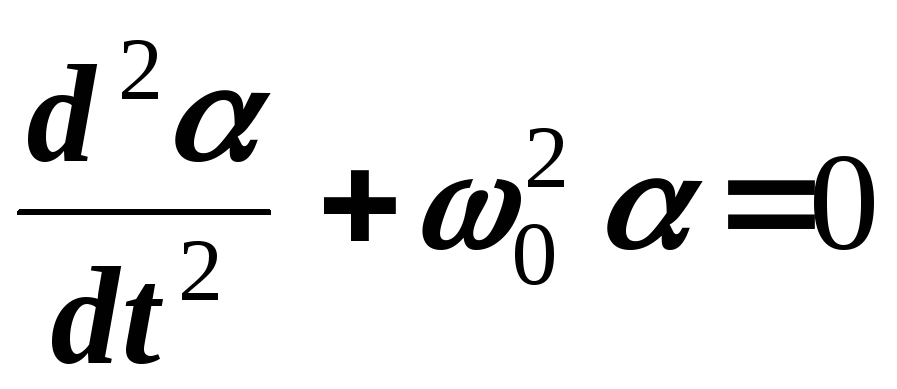, (6.3)

в якому

, (6.4)

- частота коливань, з якою зв’язаний період коливань

. (6.5)

В останній формулі

(6.6)

– так звана зведена довжина фізичного маятника, яка дорівнює довжині математичного маятника з тим самим періодом коливань.

Таким чином, щоб знайти період (чи частоту) малих коливань фізичного маятника, треба знати масу тіла , відстаньміж точкою підвішування та центром маси тіла і момент інерції тілавідносно точки підвішування.

Контрольні запитання

1. Що таке фізичний маятник?

2. Запишіть диференціальне рівняння руху фізичного маятника.

3. За яких умов рівняння руху фізичного маятника зводиться до рівняння гармонічних коливань?

4. Запишіть розв’язок диференціального рівняння (6.3).

5. Що таке зведена довжина фізичного маятника?

6. Які величини потрібно знати, щоб визначити період коливань фізичного маятника?

Методика розв’язання задач

1. Фізичний маятник розбиваємо на прості тіла, центри мас та моменти інерції яких легко знайти.

2. Початок осі суміщаємо з точкоюпідвішування маятника і спрямовуємо вздовж лінії дії сили тяжіння.

3. Визначаємо координати центра мас кожного тіла, з яких утворено маятник, та знаходимо координату його центра мас.

4. Обчислюємо момент інерції маятника відносно точки підвісу, використовуючи теорему Гюйгенса-Штейнера.

5. Знаходимо зведену довжину фізичного маятника та період його малих коливань.

Приклад. Фізичний маятник здійснює коливання відносно осі, яка проходить перпендикулярно рисунку через точку (рис. 6.2). Записати рівняння вільних малих коливань цього маятника, визначити зведену довжину фізичного маятника та період його коливань. Тіло 1 є однорідний диск масою = 2 кг та радіуса = 0,3 м, тіло 2 – однорідний стрижень масою = 3кг та довжиною =0,8 м, тіло 3 – однорідна куля масою = 15 кг та радіуса =0,2 м.

Розв’язання.Фізичний маятник утворений трьома однорідними тілами: диском, стрижнем та кулею. Диференціальне рівняння коливань фізичного маятника має вигляд

,

де .

Визначимо необхідні дані для розрахунків періоду коливань: масу маятника , відстань між віссю обертання (точкою підвішування) та центром маси і момент інерції тіла ­відносно осі обертання.

Маса фізичного маятника є сума мас його елементів

= 2 + 3 + 15 = 20 кг.

Щоб підрахувати відстань скористуємось визначенням центру мас

,

де - координати центра маси даного елемента. Розмістимо початок відліку осіхв точці підвішування, а вісьхспрямуємо вниз, як це зроблено на рис. 6.2., тоді

=

= = 0,78 м.

Момент інерції маятника відносно осі обертання є сума моментів інерції його елементів відносно цієї осі

,

де – моменти інерції диску, стрижня та кулі відносно осі обертання. Ці моменти інерції знайдемо скориставшись теоремою Гюйгенса-Штейнера

,

де – момент інерції тіла відносно осі, яка проходить через центр маси відповідного тіла паралельно осі обертання, а – відстань між центром маси тіла та віссю обертання (в нашому випадку ). Моменти інерції для тіл, які розглядаються нами при розв’язанні задач, наведені у додатку.

Отож, для диску маємо

= = 0,27 кг·м²,

для стрижня

= = 0,64 кг·м²,

для кулі

= = 15,24 кг·м².

Таким чином момент інерції маятника

= 0,27 + 0,64 + 15,24 = 16,15 кг·м².

Отримані дані дозволяють визначити зведену довжину фізичного маятника

= 1,04 м,

та період коливань маятника як

= 2,05 с.

Відповідь: = 1,04 м, = 2,05 с.