2.3. Метод наименьших квадратов применительно к производственным функциям комплексного аргумента
В параграфах 2.1 и 2.2 мы рассмотрели, как определяются коэффициенты производственных функций комплексного аргумента по статистическим данным для каждого наблюдения, и как можно интерпретировать их значения. Перед экономистами же, как правило, стоит задача: по имеющимся статистическим данным оценить параметры выбранной модели на всей имеющейся выборке. Эта задача применительно к производственной функции комплексного аргумента может быть решена двумя способами.
Первый способ заключается в нахождении коэффициентов функций по каждому из наблюдений. Затем полученные ряды значений этих коэффициентов, изменяющихся во времени, аппроксимируются с помощью наиболее подходящей модели. В самом простом случае, когда вариация коэффициентов объясняется действием только случайных факторов, рассчитывается их средняя арифметическая. Полученные значения коэффициентов подставляются в модель соответствующей производственной функции, и эта модель используется для аппроксимации.
Впрочем, можно применить и иной подход, который используется при экономическом прогнозировании с помощью производственной функции Кобба-Дугласа [78, 53]. По статистическим данным с помощью метода наименьших квадратов находят значения постоянных aи α функции (1.2.18), после чего полученные расчётные значения можно использовать для прогнозирования.
Метод наименьших квадратов применим и для предлагаемой производственной функции комплексного аргумента. Были проделаны соответствующие вычисления, но итоговые системы уравнений, решая которые можно найти оценки параметров производственной функции комплексного аргумента с помощью метода наименьших квадратов, являются достаточно громоздкими, и требуют дополнительных исследований на устойчивость. Эта задача выходит за рамки данной работы, и поэтому в ней не рассматривается. Стоит лишь отметить, что применение метода наименьших квадратов для функции комплексного аргумента вполне возможно.
Интересно, что построение с помощью метода наименьших квадратов функции Кобба-Дугласа, по данным таблицы 3 Приложения приводит к такому её виду:
.
Отрицательность одного из показателей степени противоречит условию (1.2.19), что говорит о том, что на данной базе строить функцию Кобба-Дугласа нельзя. Следовательно, использовать аналитические свойства функции в данной ситуации не удаётся.
Проще всего использовать МНК для случая элементарной производственной функции комплексного аргумента (2.1.1). Как следует из результатов раскрытия скобок функции и её группировки на вещественную и мнимую части (2.1.3), решение заключается в минимизации отклонений функции (2.1.4) от фактических значений при соблюдении условия (2.1.5). Эта задача достаточно просто формулируется, поскольку именно при соблюдении этих условий определены параметры использования ресурсов (2.1.6).
Из первой формулы в (2.1.6), когда вычисляется коэффициент использования трудовых ресурсов, легко получается следующий вид производственной функции:
.
Тогда задача нахождения оценки параметра а0с помощью МНК сводится к нахождению условия минимума суммы квадратов отклонений:
.
Эта задача имеет элементарное решение в виде:
,
Аналогично через коэффициент использования капитальных ресурсов выводится другая форма производственной функции, а именно:
.
Теперь легко найти формулу для оценки МНК коэффициента использования капитальных ресурсов:
, (2.3.1)
Полученные коэффициенты можно использовать для самых разных целей, в том числе и для прогнозирования.
Так, по исходным статистическим данным таблицы 3 Приложения для экономики современной России с помощью МНК были найдены оценки коэффициентов производственной функции (2.1.1). Она имеет вид:
. (2.3.2)
Полученная функция может использоваться как для многовариантных прогнозов, так и для некоторых аналитических выводов, относительно происходивших за 1998 – 2003 годы в России процессов.
Кроме того, по данным таблицы 5 Приложения таким же способом были найдены оценки коэффициентов производственной функции (2.1.1) для Диатомового комбината на 1999 год. Производственная функция получилась следующей:
(2.3.3)
Эта функция неплохо описывает динамику Qдля Диатомового комбината при данныхKиL, и может быть использована либо для анализа происходящих процессов, либо для прогнозирования объёмов производства.
Рассмотрим теперь, как можно применить МНК для более сложных функции комплексного аргумента – (2.2.1) и (2.2.9), на примере функции (2.2.9).
Для того чтобы упрощения и вывод формул были не громоздкими, примем:
,
,
. (2.3.4)
Тогда формула (2.2.9) примет вид:
(2.3.5)
Коэффициенты функции (2.3.5) легче всего оценить, если её предварительно линеаризовать. Прологарифмировав левую и правую части (2.3.4), получим:
(2.3.6)
Для того чтобы оценить параметры (2.3.6) с наибольшей точностью, надо использовать «принцип наименьших квадратов» [77, 572], который в нашем случае может быть выражен так:
(2.3.7)
Здесь
– расчётные значения (2.3.6), а
– фактические. Подставив в (2.3.7) значение
из (2.3.6), видим, что надо минимизировать
следующую сумму:
(2.3.8)
Раскрывая скобки в которой, получаем следующее:
(2.3.9)
Для того чтобы минимизировать эту сумму, надо взять её частные производные вначале по a, а затем – поb, и приравнять полученные выражения нулю. В результате получится следующая система нормальных уравнений:
(2.3.10)
Решая эту систему уравнений, получим формулы для расчёта aиb. Опуская промежуточные выкладки, приведём конечные формулы:
(2.3.11)
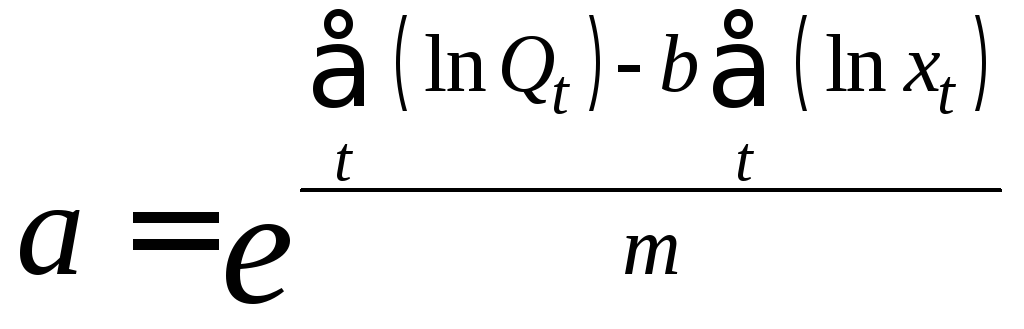(2.3.12)
С использованием обозначения (2.3.4), формулы (2.3.11) и (2.3.12) примут вид:
(2.3.13)
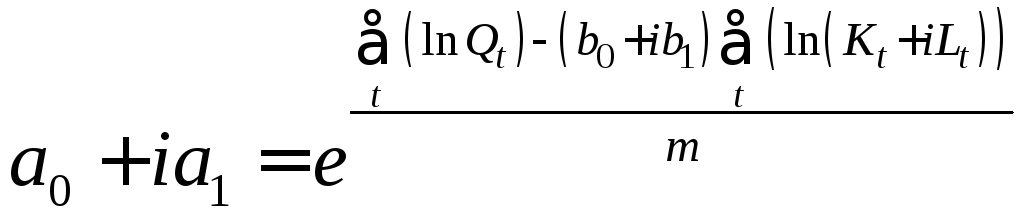(2.3.14)
Теперь, используя формулы (2.3.13) и (2.3.14), найдём параметры модели (2.2.9) по реальным статистическим данным.
По данным о Советской промышленности (таблица 2) была построена следующая производственная функция:
(2.3.15)
Эта функция очень хорошо описывает представленные данные, в частности, благодаря тому, что тенденция по изменению национального дохода близка к линейной.
Таким же образом можно построить производственную функцию комплексного аргумента и для уже использованных выше данных по Диатомовому комбинату из таблицы 5. Вот как выглядит такая функция:
. (2.3.16)
Как видно, мнимая часть показателя степени достаточно мала по сравнению с другими коэффициентами. Значит эту мнимую часть можно опустить. Тогда получится исследованная ранее функция (2.2.14), обладающая свойствами, отличающимися от функции (2.2.9). Следовательно, для анализа работы предприятия и прогнозирования стоит использовать вместо (2.3.16) функцию:
. (2.3.17)