отчёт метод Ньютона

Пермский национальный исследовательский политехнический университет

Строительный факультет

Кафедра строительных конструкций и вычислительных технологий

Лабораторные работы

по дисциплине

ИНФОРМАТИКА-2

Тема: Численные методы

Работу выполнила: Янчева А.К.

группа ПГС-11-2

Работу принял: Третьякова А.Н.

Пермь 2012

Тема: Приближенные методы решения нелинейных уравнений

1. Задание: Решить нелинейное уравнение

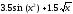
с заданной точностью =0,001 ,

используя приближённые (итерационные) методы- метод Ньютона и метод половинного деления.

2. Математическая постановка задачи:

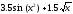
• Функция (х)=

• Рассматриваемый промежуток-;

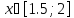• На ;

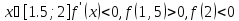• Найти 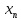, для которого.

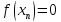3. Краткое изложение используемых численных методов:

• Метод половинного деления:

Для построения итерационного процесса циклически выполняют следующие действия:

1. Отрезок [a;b] делят пополам- ;

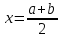2. Если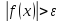переходят на пункт 3, иначе на пункт 5;

3. Если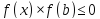принимаютa=x, иначе b=x;

4. Если переходим на пункт 1 иначе на 5;

5)В качестве приближенного решения уравнения 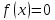выбираем .

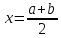• Метод Ньютона:

Для построения итерационного процесса используют следующую теорему:

Если 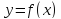на 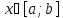удовлетворяет условиям- 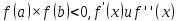существуют исохраняют свой знак, то исходя из начального приближения 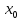, удовлетворяющего условию- , кореньуравнения можно вычислитьс точностью Ɛ по формуле: 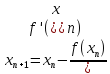. (Значение ищем до тех пор пока

5. Результаты счета на ЭВМ:

• Локализация корней:

• Уточнение корня (метод половинного деления):

• Уточнение корня (метод Ньютона):

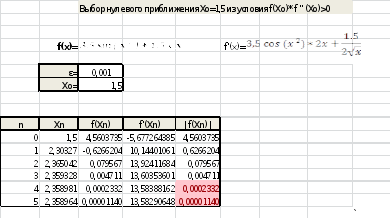
• График зависимости количества итераций от заданной точности (метод половинного деления):

График зависимости количества итераций от заданной точности