ТЕСТ МАТ 1 РЭТ 2013
.docx[a] –1
[a]
-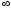
[q]3:1:
Функция
 называется четной, если для любого x
выполняется равенство
называется четной, если для любого x
выполняется равенство
[a]
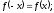
[a]
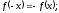
[a]
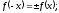
[a]
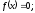
[a]
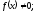
[q]3:1:
Функция
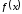 называется нечетной, если для любого x
выполняется равенство
называется нечетной, если для любого x
выполняется равенство
[a]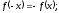
[a]
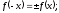
[a]
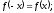
[a]

[a]
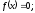
[q]3:1:
Функция
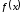 называется возрастающей, если для любых
называется возрастающей, если для любых
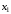 и
и
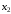 ,
таких что
,
таких что
 выполняется
неравенство
выполняется
неравенство
[a]

[a]
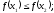
[a]
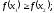
[a]
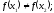
[a]
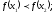
[q]3:1:
Функция
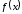 называется убывающей, если для любых
называется убывающей, если для любых
 и
и
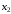 ,
таких что
,
таких что
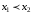 выполняется
неравенство
выполняется
неравенство
[a]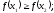
[a]
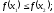
[a]
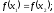
[a]
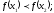
[a]
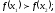
[q]3:1:
Функция
 называется строго возрастающей, если
для любых
называется строго возрастающей, если
для любых
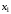 и
и
 ,
таких что
,
таких что
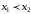 выполняется
неравенство
выполняется
неравенство
[a]
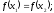
[a]

[a]
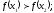
[a]
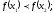
[a]
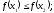
[q]3:1:
Функция
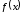 называется строго убывающей, если для
любых
называется строго убывающей, если для
любых
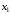 и
и
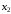 ,
таких что
,
таких что
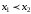 выполняется
неравенство
выполняется
неравенство
[a]
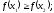
[a]
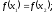
[a]
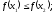
[a]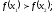
[a]
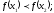
[q]3:1: Последовательность называется бесконечно малой, если ее предел равен:
[a]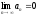
[a]
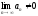
[a]
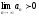
[a]
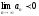
[a] Предел не существует.
[q]3:1:
Последовательность
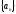 называется бесконечно большой, если:
называется бесконечно большой, если:
[a]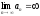
[a]
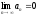
[a]

[a]
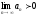
[a]
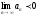
[q]3:1:
Теорема Ролля: Если функция
 непрерывна на отрезке
непрерывна на отрезке
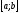 ,
дифференцируема на интервале
,
дифференцируема на интервале
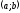 и
и
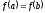 то найдется точка
то найдется точка
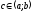 ,
такая, что выполняется:
,
такая, что выполняется:
[a]

[a]
[a]
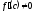
[a]
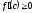
[a]
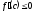
[q]3:1:
Теорема Лагранжа: Если функция
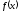 непрерывна на отрезке
непрерывна на отрезке
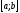 ,
дифференцируема на интервале
,
дифференцируема на интервале
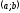 ,
то найдется точка
,
то найдется точка
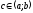 ,
такая, что
,
такая, что
[a]

[a]
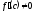
[a]

[a]
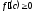
[a]
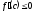
[q]3:1:
Если функция
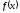 имеет положительную производную в
каждой точке интервала
имеет положительную производную в
каждой точке интервала
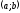 ,
то эта функция на этом интервале:
,
то эта функция на этом интервале:
[a] не возрастает
[a] убывает
[a] строго убывает
[a] не меняется
[a]возрастает
[q]3:1:
Если функция
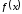 имеет отрицательную производную в
каждой точке интервала
имеет отрицательную производную в
каждой точке интервала
 ,
то эта функция на этом интервале:
,
то эта функция на этом интервале:
[a]убывает
[a] строго возрастает
[a] не убывает
[a] возрастает
[a] не меняется
[q]3:1:
Точка
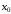 из области определения функции
из области определения функции
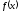 называется точкой минимума этой функции,
если существует такая
называется точкой минимума этой функции,
если существует такая
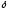 -
окрестность точки
-
окрестность точки
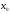 ,
что для всех
,
что для всех
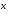 из
этой
из
этой
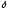 -
окрестности выполняется неравенство...
-
окрестности выполняется неравенство...
[a]
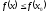
[a]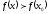
[a]
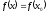
[a]
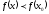
[a]
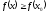
[q]3:1:
Теорема Коши: Если функции
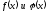 непрерывны на отрезке
непрерывны на отрезке
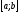 и дифференцируемы во всех его внутренних
точках, причем
и дифференцируемы во всех его внутренних
точках, причем
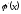 в этих точках не обращается в нуль, то
в этом интервале существует хотя бы
одно значение
в этих точках не обращается в нуль, то
в этом интервале существует хотя бы
одно значение
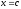 ,
для которого выполняется равенство:
,
для которого выполняется равенство:
[a]

[a]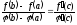
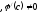
[a]
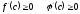
[a]
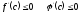
[a]
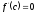
[q]3:1:
Найти
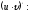
[a]
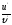
[a]
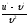
[a]
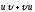
[a]
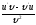
[a]
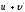
[q]3:1:
Найти
![]()
[a]
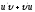
[a]
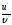
[a]
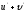
[a]
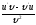
[a]

[q]3:1:
Найти
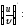
[a]
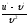
[a]

[a]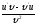
[a]
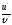
[a]
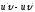
[q]3:1: Для раскрытия, каких неопределенностей можно пользоваться правилом Лопиталя ?
[a]
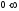
[a] - или 1
[a] 1 или -
[a]

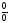 или
или
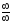
[a]
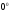 или 0
или 0
[q]3:1:
Найдите следующий предел
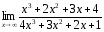
[a] 4;
[a]
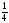 ;
;
[a] 1;
[a] 0;
[a]
[q]3:1:
Найти
 ,
если
,
если
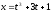 ;
;

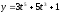
[a]
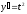
[a]
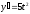
[a]

[a]
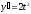
[a]
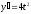
[q]3:1:
Найти
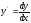 ,
если
,
если
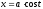 ;
;

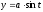
[a] –ctg t
[a] tg t
[a] [a] -tg t
[a] ctg t
[a] a
[q]3:1:
Пусть в некоторой окрестности точки
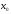 (кроме, быть может, самой точки
(кроме, быть может, самой точки
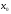 )
функции
)
функции
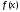 и
и
 дифференцируемы
и
дифференцируемы
и
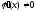 .
Если
.
Если
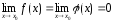 или
или
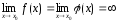 ,
то
,
то
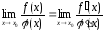 .
Какая это теорема?
.
Какая это теорема?
[a] теорема Лопиталя
[a] теорема Даламбера
[a] теорема Ферма
[a] теорема Ролля
[a] теорема Коши
[q]3:1:
Если функция f(x)
непрерывна на отрезке [a,
b],
дифференцируема в интервале (a,
b)
и f(a)
= f(b),
то в интервале (a,
b)
найдется хотя бы одно значение
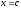 ,
при котором
,
при котором
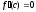 .
Какая это теорема?
.
Какая это теорема?
[a] теорема Лагранжа
[a] теорема Коши
[a] теорема Ролля
[a] теорема Ферма
[a] теорема Лопиталя
[q]3:1:
Если функции
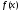 и
и
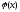 непрерывны
на отрезке [a,
b]
и дифференцируемы в интервале (a,
b),
причем
непрерывны
на отрезке [a,
b]
и дифференцируемы в интервале (a,
b),
причем
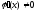 ,
то в этом интервале найдется хотя бы
одно значение
,
то в этом интервале найдется хотя бы
одно значение
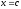 ,
при котором
,
при котором
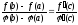 ,
где
,
где
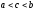 .
Какая это теорема?
.
Какая это теорема?
[a] теорема Лагранжа
[a] теорема Ролля
[a] теорема Лопиталя
[a] теорема Коши
[a] теорема Ферма
[q]3:1:
Найти производную
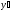 функции
функции
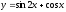 :
:
[a]
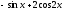
[a]
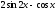
[a]
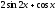
[a]
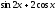
[a]
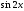
[q]3:1:
Найти производную
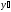 функции
функции
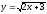 :
:
[a]
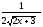
[a]
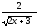
[a]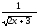
[a]
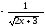
[a]
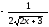
[q]3:1:
Найти
производную
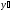 функции
функции
 :
:
[a]
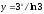
[a]
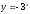
[a]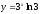
[a]

[a]