Отношение — это естественный критерий качества

У неспециалистов в области цифровой связи может возникнуть вопрос о полезности параметра. Отношение — это удобный критерий качества для аналоговых систем связи: числитель представляет меру мощности сигнала, которую желательно сохранить, а знаменатель — ухудшение вследствие электрических помех. Более того, отношение интуитивно воспринимается как мера качества. Итак, почему в цифровых системах связи мы не можем продолжать использовать отношение как кри­терий качества? Зачем для цифровых систем нужна другая метрика — отношение энергии бита к спектральной плотности мощности шума? Объяснению этого вопроса и посвящен данный раздел.

В разделе.4 мощностной сигнал определялся как сигнал с конечной средней мощностью и бесконечной энергией. Энергетический сигнал определялся как сигнал с нулевой средней мощностью и конечной энергией. Такая классификация полезна при сравнении аналоговых и цифровых сигналов. Аналоговый сигнал мы относим к мощностным сигналам. Почему это имеет смысл? Об аналоговом сигнале можно ду­мать как о сигнале, имеющем бесконечную длительность, который не требуется раз­граничивать во времени. Неограниченно длительный аналоговый сигнал содержит бесконечную энергию; следовательно, использование энергии — это не самый удоб­ный способ описания характеристик такого сигнала. Значительно более удобным па­раметром для аналоговых волн является мощность (или скорость доставки энергии).

В то же время в системах цифровой связи мы передаем (и принимаем) символы путем передачи некоторого сигнала в течение конечного промежутка времени, време­ни передачи символа . Сконцентрировав внимание на одном символе, видим, что мощность (усредненная по времени) стремится к нулю. Значит, для описания харак­теристик цифрового сигнала мощность не подходит. Для подобного сигнала нам нуж­на метрика, "достаточно хорошая" в пределах конечного промежутка времени. Дру­гими словами, энергия символа (мощность, проинтегрированная по ,) — это гораздо более "удобный параметр описания цифровых сигналов.

То, что цифровой сигнал лучше всего характеризует полученная им энергия, еще не да­ет ответа на вопрос, почему — это естественная метрика для цифровых систем, так что продолжим. Цифровой сигнал — это транспортное средство, представляющее цифро­вое сообщение. Сообщение может содержать один бит (двоичное сообщение), два (четверичное), ..., 10 бит (1024-ричное). В аналоговых системах нет ничего подобного та­кой дискретной структуре сообщения. Аналоговый информационный источник — это бес­конечно квантованная непрерывная волна. Для цифровых систем критерий качества дол­жен позволять сравнивать одну систему с другой на битовом уровне. Следовательно, опи­сывать цифровые сигналы в терминах практически бесполезно, поскольку сигнал может иметь однобитовое, 2-битовое или 10-битовое значение. Предположим, что для данной вероятности возникновения ошибки в цифровом двоичном сигнале требуемое от­ношение равно 20. Будем считать, что понятия сигнала и его значения взаимозаме­няемы. Поскольку двоичный сигнал имеет однобитовое значение, требуемое отношение на бит равно 20 единицам. Предположим, что наш сигнал является 1024-ричным, с теми же 20 единицами требуемого отношения . Теперь, поскольку сигнал имеет 10-битовое значение, требуемое отношение 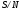на один бит равно всего 2. Возникает во­прос: почему мы должны выполнять такую цепочку вычислений, чтобы найти метрику, Представляющую критерий качества? Почему бы сразу не выразить метрику через то, что, нам действительно надо, — параметр, связанный с энергией на битовом уровне,

В заключение отметим, что поскольку отношение является безразмерным, таким же является и отношение . Для проверки можно вычислить единицы измерения:

.

Детектирование двоичных сигналов в гауссовом шуме

Критерий принятия решения, используемый в этапе 2 описывался форму­лой (7.7) следующим образом:

Популярный критерий выбора порога для принятия двоичного решения в выраже­нии (3.7) основан на минимизации вероятности ошибки. Вычисление этого минимального значения ошибки = начинается с записи связи отношения плотностей условных вероят­ностей и отношения априорных вероятностей появления сигнала. Поскольку плотность условной вероятности также называется функцией правдоподобия формулировка

(7.3)

есть критерием отношения функций правдоподобия (см. приложение Б). В этом неравен­стве и являются априорными вероятностями передачи сигналов и , a и — две возможные гипотезы. Правило минимизации вероятности ошибки (формула (3.3)) гласит, что если отношение функций правдоподобия больше отноше­ния априорных вероятностей, то следует выбирать гипотезу .

В разделе Б.3.1 показано, что при = и симметричных функциях правдо­подобия (i=l, 2) подстановка формул (3.5) и (3.6) в формулу (3.3) дает

(7.4)

где — сигнальный компонент при передаче, а — сигнальный компонент при передаче . Порог , представленный выражением , — это опти­мальный порог для минимизации вероятности принятия неверного решения в этом важном частном случае. Описанный подход называется критерием минимальной ошиб­ки.

Для равновероятных сигналов оптимальный порог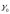, как показано на рис, 3.2, проходит через пересечение функций правдоподобия. В заключение отметим, что поскольку отношение является безразмерным, таким же является и отношение . Для проверки можно вычислить единицы измерения:

.

Основная литература 4[155:174].

Дополнительная литература 13[78:96].

Контрольные вопросы

1.Что такое отношение сигнал\шум?

2. Как детектируется двоичные сигналы в шуме?

3.Что такое критерий минимальной ошибки?

Лекция №8 (2 час.)

Детектирование двоичных сигналов в гауссовом шуме

Согласованный фильтр

Согласованный фильтр (matched filter) — это линейное устройство, спроектированное, чтобы давать на выходе максимально возможное для данного передаваемого сигнала отношение сигнал/шум. Предположим, что на вход линейного, инвариантного во времени (принимающего) фильтра, за которым следует устройство дискретизации, подается известный сигнал s(t) плюс шум AWGN n(t). В момент времени t = Т сигнал на выходе устройства дискретизации z(T) состоит из компонента сигнала 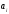, и компонента шума. Дисперсия шума на выходе (средняя мощность шума) запи­сывается как . Отношение мгновенной мощности шума к средней мощности шума, (S/N)_T, в момент t = Т вне устройства дискретизации на этапе 1 равно следующему:

(8.1)

Нам нужно найти передаточную функцию фильтра с максимальным отношением (SIN)_T. Сигнал на выходе фильтра можно выразить через передаточную функцию фильтра H(f) (до оптимизации) и Фурье-образ сигнала на входе

(8.2)

где S(f) — Фурье-образ сигнала на входе, s(t). Еели двусторонняя спектральная плот­ность мощности шума на входе равна , то с помощью формул (1.19) и (1.53) мощность шума на выходе можно записать следующим образом:

(8.3)

Объединяя формулы (3.45) и (3.47), получаем выражение для (S/N):

(8.4)

б)

Рис. 8.1. Межсимвольная интерференция в процессе детектирование:

а) типичная низкочас­тотная цифровая система; б) эквивалентная модель

Здесь характеризует передающий фильтр, — фильтрацию в канале, а — принимающий/выравнивающий фильтр. Таким образом, характеристика представляет передаточную функцию всей системы, отвечающую за все этапы фильтрации в различных местах цепочки передатчик-канал-приемник. В бинар­ной системе, использующей какую-нибудь распространенную кодировку РСМ, например NRZ-L, детектор принимает решение относительно значения символа путем сравнения выборки принятого импульса с порогом.

Например, детектор, изображенный на рис. 3.15, решает, что была послана двоичная единица, если принятый импульс положителен, или двоичный нуль — в противном случае. Вследствие системной фильтрации принятые импульсы могут перекрываться, как показано на рис. 3.15, б. Хвост импульса может "размываться" на соседний ин­тервал передачи символа, таким образом, мешая процессу детектирования и по­вышая вероятность появления ошибки; подобный процесс получил название межсимвольной интерференции (intersymbol interference — ISI). Даже при отсутст­вии шумов воздействие фильтрации и искажение, вызванное каналом, приводят к возникновению IS1. Иногда функция задается, и задача состоит в определе­нии и , минимизирующих ISI на выходе .

Согласованные и обычные фильтры

Обычные фильтры отсекают нежелательные спектральные компоненты принятого сигнала при поддержании некоторой точности воспроизведения сигналов в выбран­ной области спектра, называемой полосой пропускания (pass-band). В общем случае эти фильтры разрабатываются для обеспечения приблизительно одинакового усиления, линейного увеличения фазы в зависимости от частоты в пределах полосы пропуска­ния и минимального поглощения в остальной части спектра, именуемой полосой за­граждения (stop-band). Согласованный фильтр имеет несколько иные "проектные приоритеты", направленные на максимизацию отношения сигнал/шум известного сигнала при шуме AWGN. В обычных фильтрах используются случайные сигналы, и результат фильтрации определяется только полосами сигналов, тогда как согласован­ные фильтры предназначены для известных сигналов, имеющими случайные парамет­ры (такие, как амплитуда и время). Согласованный фильтр можно рассматривать как шаблон, который согласовывает обрабатываемый сигнал с известной формой. Обыч­ный фильтр сохраняет временную или спектральную структуру сигнала. Согласован­ный фильтр, наоборот, в значительной степени модифицирует временного структуру путем сбора энергии сигнала, которая согласовывается с его шаблоном, и в заверше­ние каждого интервала передачи символа представляет результат фильтрации в виде значения максимальной амплитуды. Вообще, в цифровой связи приемник обрабаты­вает поступающие сигналы с помощью фильтров обоих типов. Задачей обычного фильтра является изоляция и извлечение высокоточной аппроксимации сигнала с по­следующей передачей результата согласованному фильтру. Согласованный фильтр на­капливает энергию принятого сигнала, и в момент взятия выборки (t = T) на выход фильтра подается напряжение, пропорциональное этой энергии, после чего следует детектирование и дальнейшая обработка сигнала.