4Кесте.

Карталардың номенклатурасы.

Масштабтары	Парақ өлшемдері			Номенклатурасы
	Ендік	Бойлық
1:1000 000	4	6	K-43
1:100000	20`	30`	K-43-64
1:50000	10`	15	K-43-64-Б
1:25000	5`	7`30``	K-43-64-Б-а
1:10000	230`	3`45``	K-43-64-Б-а-4
1:5000	115`	1`52``,5	K-43-64 (256)
1:2000	25``	37``,5	K-43-64 (256-4)

Масштабтары 1: 5000ч1:500 аралығындағы план парақтарының номенклатуралары мен өлшемдері 5-кестеде келтірілген.

5-кесте.

Пландардың номенклатуралары

Масштабтар	Планшет номенклатурасы	Рамалардың өлшеулері, см
1:5 000	4	40Ч40
1:2 000	4-5	50Ч50
1:1 000	4-Б-IV	50Ч50
1: 500	4-Б-15	50Ч50

Жер бетін цифр түрінде бейнелеу:

Есептеу техникаларының және автоматты сызба аспаптарының (графиктік сызба жабдығы) дамуы әртүрлі инженерлік есептерді тез шешу үшін автоматтандырылған сызба жүйелерін құруға әкеледі. Бұл есептердің жартысы топографиялық пландар мен карталарды пайдалана отыра шешіледі. Осы тұрғыда жергілікті жердің топографиясы туралы мәліметтерді цифрлы түрде компьютерде сақтау және керек болған жағдайда жедел пайдалана білу мүмкіндігі туды.

Компьютер жадында жергілікті жердің мәліметтері Х,Ү,Н, координаталары бар көптеген нүктелер түрінде сақталады. Осындай координаталары белгілі көптеген нүктелер жер бетінің цифрлық моделін (жцм) құрайды.

Мазмұнына қарай жердің цифрлық моделі ситуациялық цифрлы модель (сцм) және бедерлік цифрлы модель (БЦМ) болып бөлінеді.

Ситуацияның барлық элементтері Х және Ү координаталары белгілі нүктелермен бейнеленіп, жергілікті жердің контурын және заттардың орнын анықтайды. Бедерлік цифрлы модель жер бетінің топографиялық жағдайын сипаттайды, яғни жердің бедерін қажетті түрде бейнелейтін Х, Ү, Н координаталары белгілі көптеген нүктелер арқылы беріледі.

Жер бедерінің әрқилылығына байланысты оны цифр түрінде жан-жақты бейнелеу өте күрделі мәселе.

Сондықтан шешілетін мәселеге байланысты және жер бедерінің сипатына қарай цифрлы модельдерді жасаудың әртүрлі тәсілдері қолданылады. Мәселен, бедерлік цифрлы модельді жер учаскесінің ауданында біркелкі орналасқан квадраттар немесе дұрыс үшбұрыштар төбелерінің Х,Ү, Н координаталарының кестесі түрінде құралады.

Төбелердің арақашықтықтары жер бедерінің түрінде (пішініне) және шешілетін есепке байланысты алынады.

Цифрлы модель жер бедерінің ерекше нүктелері орналасқан (су айырғыш, қайқы бел және т.б.) жерлер немесе горизонтальдар координаталарының кестесі түрінде де бейнеленеді. Цифрлы модель нүктелерінің координаталары мәндерін пайдалана отыра, жер бедерін компьютерлік программа арқылы бейнелеп, адам жер учаскесінің кез-келген нүктесінің биіктігін анықтауға болады.

Өзіндік тексеру сұрақтары:

1.Номенклатура деген не?

2.Трапеция емес квадраттық бөлу қайда қолданылады?

3.Карталардың номенклатурасы нені білдіреді?

4.Пландардың номенклатурасы нені білдіреді?

5. Жер қисықтығының горизонталь және вертикаль арақашықтықтарға тигізетін әсері?

6. Цифрлы карталар қалай жасалынады?

Әдебиеттер:

1.Қалабаев К.Б., Нурпейсова М.Б., Жарқымбаев Б.М. «Картамен жұмыс істеу» Алматы:

КазПТИ 1990. 12б.

2.Селиханович В.Г. «Геодезия» М.: Недра, 1981ж.

Дәріс №7. Пландар мен карталардағы рельеф бейнелеу әдістері.

Дәріс мақсаты: Рельефті горизонталь арқылы бейнелеудің мәні. Горизонтальдар, горизонталь белгілері туралы жалпы түсініктер. Горизонталь әдісі.

Кілт сөзі: Рельеф, төбе, тау, ой-шұңқыр, жота, сай, өркеш төбелер, суайрық, сужинақ.

Қысқаша мазмұн:

Горизонталь деп бірдей биіктіктегі нүктелерді бір-бірімен қосатын тұйық қисық сызықты айтады.

Көршілес қиятын жазықтықтың арасындағы арақашықтықты һ рельеф қимасының биіктігі деп атайды. План мен картада рельеф қимасының биіктігі жер бетінің рельефінің сипатына және түсіру 1 масштабына байланысты алынады. Берілген картада және планда қиманың биіктігі һ тұрақты болады.

Рельефті оңай оқу және ылдидың (төмендеудің) бағытын анықтау үшін горизонтальдарға ылдидың өзгерісіне перпендикуляр сызықша-бергштрих белгісін қояды.

Топографиялық картада көлбеулігі 45″-тан аспайтын ылдиларды горизонтальмен белгілейді, ал ол шамадан үлкен болса, яғни тік құламаларды арнаулы шартты белгілермен көрсетеді. Карта мен планда бейнеленген рельефті санмен өрнектелген төбенің биіктігімен, тереңдікпен және басқа қосымша биіктік белгілермен сипаттауға болады.

Карта мен пландағы рельефтің бейнелері. Жердің физикалық бетінің өзгерісін (кедір-бұдырларын) рельеф арқылы айқындауға болады. Рельефтің сипатына байланысты Жердің беті жазық, төбелі және таулы болып бөлінеді. Жер бетінің негізгі рельефіне жататындар: төбе ой-шұңқыр, жота, сай және өркеш төбелер.

Төбе, тау – конус немесе купол тәрізді болған биік жер беті. Таудың ең биік жері таудың төбесі болып саналады. Төбеден жан-жаққа тараған ылдиды таудың құламасы немесе жоны деп атайды. Жонның жазыққа ауысқан жері таудың табаны болады. Егер биіктігі 200 метрден төмен болып, пішіні жазықтық құламамен құрылса, оны төбе деп атаймыз. Ал биіктігі 200 метрден жоғары тік құламадан құрылған рельефтің пішіні тау болады. Тау мен төбелер тұйық горизонтальмен және табанына қарай бағытталған бергштрихпен белгіленеді.

Ой-шұңқыр- тауға (төбеге) қарама-қарсы рельефтің бейнесі, пішіні кесе тәріздес еңіскен жердің беті. Ойдың ең төменгі бөлігін, оның түбі деп атайды. Ойдың бүйір беттері ылдидан (жонынан) тұрады, олардың жер бетімен өту сызығын ойдың жиегі дейді. Кішкентай ойларды шұңқыр деп атайды. Ой да тау сияқты тұйық горизонтальмен бейнеленеді, бірақ бұл жағдайда бергштрихтері ойдың түбіне бағытталған.

Жота (арқа) – тау мен төбеден бөлініп шығып, биіктігі бір бағытпен өзгерген рельефтің пішіні. Жотаның басты элементтері суайрық сызықтары, жоны және табаны. Суайрық сызықтары жотаның бойымен ең биік нүктелерді қосады. Жота дөңес горизонтальмен бейнеленеді, оның дөңестігі жердің төмендеу жағына бағытталған.

Сай – бір бағытпен өзгерген еңістік (ойлы) жер. Сайдың жиегінен екі бүйір беті (жоны) төмендеп келіп, түбінде сужинағыш сызығын немесе тальвегін құрайды. Сайдың түрлері: алқап-жазық құламалы енді сайлар, жар (терең сай, таулы жерде шатқал) – тік құламалы тар сайлар. Сай ойыс горизонтальдармен бейнеленеді, ойыстың бағыты төмен жерлерге қарай бағытталған, тік жарлар арнаулы шартты белгілермен бейнеленеді.

Өркеш төбелер – екі төбенің жотасының төмендеген жері (немесе иілуі). Өркеш төбелерден бір-біріне қарама-қарсы бағытта екі сай басталады. Таулы жерлерде өркеш таулардың екі қарама-қарсы жонның арасында жол қатынасы- асуларымен жасалады. Өркеш төбелер қарама-қарсы бағытталған дөңес горизонтальдармен бейнеленеді. Таудың төбесі, ойдың түбі, өркеш төбелердің ең төменгі нүктелері және иілген жердің нүктелері – рельефке тән нүктелер, ал суайрық және сужиналғыш сызықтары – рельефке тән сызықтар. Рельефтің кез-келген пішіні көлбеу беттерден, құламалардан құралады, олар бірқалыпты, дөңес, ойыс және аралас болып бөлінеді.

Бірқалыпты құламаларда горизонтальдардың арасы бірдей болып келеді, дөңес құламаларда төбесіне қарағанда табанының горизонтальдарының арасы кіші болады, ал ойыс құламалар да, керісінше, төбеге жақын жерлерде горизонтальдың арасы кіші болады да, табанында ұзарып үлкейеді. Сондықтан топографиялық картада горизонтальдардың өзгерісі арқылы құламалардың пішінін білуге болады.

Горизонтальдардың қасиеттері. Рельефті горизонтальмен бейнелеудің мәніне байланысты олардың басты қасиеттері шығады.

1. Бір горизонтальдың үстіндегі кез-келген нүктелер бірдей биіктіктерде болады.

2. Карта мен пландағы тұйық горизонтальдардың жиынтығы төбені немесе ойды көрсетеді.

3. Карта мен планда горизонтальдар үздіксіз сызықтар болады. Ол сызықтар тек терең жарлар орналасқан жерлерде ғана үзіледі.

4. Горизонтальдар бір-бірімен қиылыспайды және тарамдалмайды. Тек шығып, ілініп тұрған жартастарды горизонтальмен бейнелегенде, олар қиылысуы мүмкін, сондықтан құздарды (жартастарды) бейнелегенде арнайы шартты белгілерді қолданады.

5. Горизонтальдың арасындағы ұзындық құламаның көлбеулігін сипаттайды.

Рельеф қимасының биіктігінің жатыс сызығына қатынасын сызықтың еңістігі деп атайды.

і = Һ / d (10)

Еңістік процентпен не промиллмен (мыңнан бір бөлігі) көрсетіледі.

Мына формула арқылы құламаның көлбеулігін оңай анықтауға болады:

tgv = i = h / d (11)

6. Суайрық пен сужинақ сызықтары горизонтальдарды тікбұрышпен кеседі.

7. Горизонтальдардың биіктік шамасы рельефтің қимасының биіктігіне тең болады.

Мысалы, рельеф қимасының биіктігі һ=1, горизонтальдың биіктігі 140, 141, 142, 143 және т.т.; һ=2,5м, 140, 142,5, 145,0, 147,5 және т.т.

Карта мен планды оқығанда, сонымен қатар оларды жасағанда горизонтальдар, бергштрихтер, биіктік жазулары және т.б. рельефке байланысты шартты белгілер қоңыр түсті тушпен бейнеленеді.

Өзіндік тексеру сұрақтары:

1.Горизонтальдар дегеніміз не?

2.Рельеф қимасының биіктігі дегеніміз не?

3.Бергштрих белгісін не үшін қойады?

4.Жер бетінің негізгі рельефіне жататындарды атаңыз?

5.Горизонтальдардың қасиеттері.

Әдебиеттер:

1.Атымтаев Б.Б., Пентаев Т.П. «Инженерлік геодезия» Алматы-2005ж.

2.Багратуни Г.В., Ганьшин В.В., Данилевич Б.Б. «Инженерная геодезия» М.: Недра 1984ж.

Дәріс №8. Сызықтарды бағдарлау.

Дәріс мақсаты: Сызықтарды бағдарлау.Сызықтарды осьтік меридиан бойынша бағдарлау жолдарын студенттерге үйрету.

Кілт сөзі: Бағдарлау, географиялық азимут, географиялық румб, магниттік меридиан, компас, солтүстік шығыс, оңтүстік шығыс, солтүстік батыс, оңтүстік батыс.

Қысқаша мазмұн:

Жер бетінде орналасқан заттарды, сызықтарды бағдарлау дегеніміз, олардың меридианнан бастап есептелген бағытын анықтау. Бағдарлау негізінде негізгі тұрақты бағыт географиялық, магниттік меридиан, сондай-ақ, осьтік меридиан (x-осі) немесе параллель сызықтар да алынады. Жергілікті жердегі заттарды компас немесе буссоль арқылы бағдарлауға болады. Компастың (буссольдық) шеңбері 360°−қа бөлінеді. Меридианың солтүстік басынан бір затқа қарай сағат тілінің бағытымен есептелген жергілікті немесе картадағы горизонталь бұрышы азимут деп аталады, ал азимут арабшадан аударғанда «бағытты» білдіреді.

Мысалы, егер бір зат (тригонометриялық белгі) біздің солтүстік шығыс – СШ жағымызда тұрса, онда азимут 60°−қа, оңтүстік шығысында ОШ болса, 150°−қа тең деп айтуға болады:

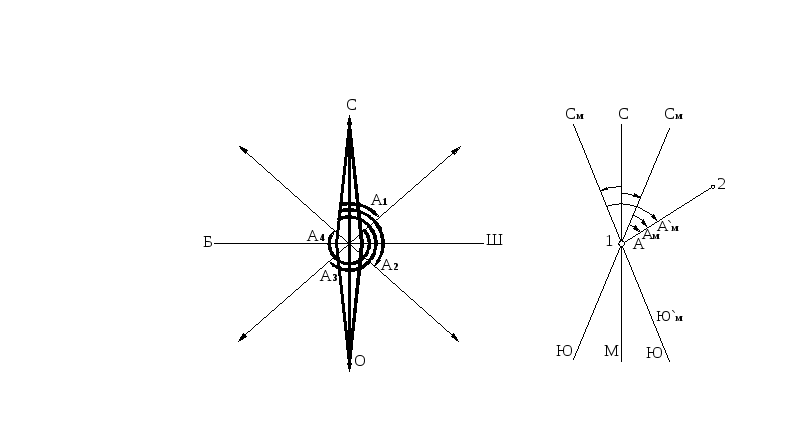
10-сурет. Сызықтарды бағдарлау.

Берілген бір нүктеде меридианды астрономия тәсілімен тапсақ, онда меридиан негізгі (географиялық), ал магнит стрелкасы арқылы тапсақ, магниттік меридиан болып аталады.

Осыған сәйкес өлшенетін азимутта негізгі – А_н және магниттік А_м азимут болып келеді. Әр нүктенің магниттік меридианы оның географиялық негізгі меридианына сәйкес келмейді; Олардың стрелкасы бұрыш магнит стрелкасының бұрылу бұрышы (δ) деп аталады. Егер стрелканың солтүстік ұшы негізгі меридианнан шығысқа қарай бұрылса, батыстың бұрылу бұрышы болады, шығыстың бұрылу оң (+), ал батыстың бұрылу теріс(–) болып келеді. Егер магнит тілінің бұрылу бұрышы δ–ның мәні белгілі болса, магниттік азимутқа мына төмендегі формуланы пайдаланып, көшуге болады:

А_н=A_м+ δ_ш;

А_н=A_м=δ_б; (12).

мұндағы δ_ш, δ_б – магнит тілінің шығыс және батыс бұрыштары.

Егер жоғарыда айтылғандай шығыс бұрылуды оң (+), ал батыс бұрылуды теріс (–) деп қабылдасақ, онда екі жағдайда да мына формуланы аламыз:

А=А_м+δ (13).

Магнит тілінің бұрылуы жер бетінің әр жерінде әртүрлі болып келеді. ТМД елдерінде δ – ның шамасы 0°−тан 20°−ға жуық шамаға екі жаққа ауытқиды. Демек сызықтарды магниттік меридиан бойынша бағдарлау тек қана жер бетінің шағын учаскелерінің пландарын жасағанда ғана қолданылады.

Кез-келген жердің өзіне тән магниттік бұрылуын жақын жердегі метеорологиялық стансадан немесе сол жердің топографияық картасынан алуға болады.

Сызықтарды осьтік меридиан бойынша бағдарлау:

Карталар мен пландар координаталардың зоналық тік бұрышты жүйесінде жасалатындықтан, геодезияда дирекциондық бұрыштар жиі қолданылады. Дирекциондық бұрыш (α) деп осьтік меридианның солтүстік жағынан сағат тілінің бағытымен бағдарланғыш сызыққа дейінгі горизонталь бұрышты айтады (11, a - сурет).

Дирекциондық бұрыштар азимуттар сияқты 0°−тан 360°−қа дейін өзгереді.

11– суреттегі АВ бағытының дирекциондық бұрышы α_АВ тура, ВА бағытының бұрышы α_ВА кері дирекциондық бұрыштар болып есептеледі. Осы суреттен:

α_кері= α_тура+180° (14)

11-сурет. а) тура және кері азимуттар; ә) дирекциондық бұрыштар;

яғни, кері диррекциондық бұрыш пен тура диррекциондық бұрыштардың айырмашылығы 180°−қа тең. Жалпы алғанда мына формуланы пайдаланған дұрыс,

α_кері= α_тура+180° (15).

Геодезиялық және маркшейдерлік өлшеулердің барлығы да сызықтар диррекциондық бұрыштар арқылы бағдарланады, өйткені сызықтың диррекциондық бұрышы жер бетінің кез-келген нүктесінде өз мәнін өзгертпейді, яғни тұрақты. Бұл – диррекциондық бұрыштардың азимутқа қарағандағы бір ерекшелігі. Ал, тура және кері азимуттар арасындағы байланысты мына формуладан көруге болады:

А_кері= А_тура+180°+γ (16).

мұндағы γ – меридиандардың жақындасу бұрышы, яғни меридиан мен осьтік меридиан (x) немесе оған параллель сызық арасындағы бұрыш. Бұл бұрыштың мәні әр нүктенің 0-дік меридианнан қашықтауына байланысты ауытқып отырады. 9-сурет бойынша АВ сызығының негізгі азимуты А_н, ал диррекциондық бұрышы α_АВ десек, онда:

γ= α_АВ− А_н (17).

яғни, нақты бір нүктедегі кез-келген сызықтың азимутымен диррекциондық бұрышының айырмашылығы (γ – осы нүктедегі негізгі меридиан мен осьтік меридианның жақындасуына тең).

Егер дирекциондық бұрыш − (α) белгілі болса, онда негізгі азимутты мына формула арқылы анықтайды: А_н=α+γ (18)

Осьтік меридианнан батысқа қарай орналасқан нүктелер үшін меридиандардың жақындасу бұрышының мәні теріс болып келеді.

Өзіндік тексеру сұрақтары:

1.Жер бетіндегі сызықтарды бағдарлау деген не?

2.Сызықтық азимуты деген не?

3.Негізгі және магниттік азимуттардың айырмашылығы неде?

4.Дирекциондық бұрыш дегеніміз не және оның өзгеру шектері қандай?

Әдебиеттер:

1.Нурпейсова М.Б. «Геодезия», (дәрістер жинағы) 1 және 2 бөлім. КазПТИ, 1990ж-102б.

2.Закатов П.С. «Инженерная геодезия» М.: Недра, 1986ж.

Дәріс №9. Румбтар және олардың дирекциондық бұрыштармен байланысы.

Дәріс мақсаты: Румбтар және олардың дирекциондық бұрыштармен байланысы. Келесі сызықтың дирекциондық бұрышын анықтау. Тура және кері геодезиялық есептерді студенттерге көрсету және түсіндіру.

Кілт сөзі: Румб, тригонометрия, ширек, тура және кері геодезиялық есеп, координата, полигон, дирекциондық бұрыш.

Қысқаша мазмұн:

Сызықтарды бағдарлау және өлшеу нәтижелерін өңдеу кезінде румб деп аталатын сүйір бұрыш пайдаланылады. Шамасы 0°−тан 90°−қа дейін өзгеретін осьтік меридианның оңтүстік және солтүстік жағынан екі жаққа қарай бір нақты сызыққа дейін есептелетін сүйір бұрышты румб дейді.

12-суретте әр ширекте алынған төрт сызықтың румбтары көрсетілген. Бағытты румб арқылы табу үшін оның сан мәнінің алдына ширектің аты көрсетіледі.Мысалы, СШ (солт.шығыс), ОШ (оңт.шығыс), ОБ (оңт.батыс), СБ (солт.батыс) деп белгіленеді және осы суреттен әрбір ширекте румбтар (кестелік бұрыштар) мен дирекциондық бұрыштар арасындағы байланысты көруге болады. Ол байланысформулалары 6-кестеде берілген.

12-сурет. Румбтар және дирекциондық бұрыштар арасындағы байланыс.