Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Киевская государственная академия водного транспорта им. Конашевича-Сагайдачного

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

matametika_bevz_standart_1 / matametika_bevz_standart

.pdf

Скачиваний:

149

Добавлен:

08.02.2016

Размер:

5.51 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 167 8 9 10 11 12 13 14 15 16 > Следующая >>>

1Ðîçäië

293.Яке із чисел більше:

а)

б)

294. Обчисліть за допомогою мікрокалькулятора:

а) 3,20,2;

б) 0,52–1,3; в) 132,7 2,5; г) 3,5–4 62,3.

295.Запишіть за допомогою коренів вираз:

296.Запишіть без знаків кореня вираз:

297.Запишіть за допомогою коренів вираз:

298. Спростіть вираз:

299. Подайте у вигляді степеня:

Обчисліть (300–303).

300.

СТЕПЕНІ З РАЦІОНАЛЬНИМИ ПОКАЗНИКАМИ § 7

301.

302.

303.

Спростіть вираз (304–307).

304.

305.

306.

307.

1Ðîçäië

308.Скоротіть дріб:

309.Доведіть, що для натурального n:

310.Розв’яжіть рівняння:

а) 4х(х – 1) = 3; б) z(z – 1) = 20.

311.Зобразіть за допомогою діаграм співвідношення між поняттями «функції», «парні функції», «непарні функції».

312.Побудуйте графік функції: а) у = 3х; б) у = х–2; в) .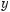

§ 8. Степеневі функції

Функція, яку можна задати формулою у = хα, де х – аргумент, а α – дане число, називається степеневою.

Уже відомі вам функції у = х2 і у = х3 (див. табл. 1, с. 34) – приклади степеневих функцій. Подібні властивості мають також усі інші степеневі функції з натуральними показниками α. На малюнках 37 і 38 подано графіки степеневих функцій у = х4 і у = х5. Кожна степенева функція з натуральним показником степеня визначена на множині всіх дійсних чисел R.

Мал. 37

Мал. 38

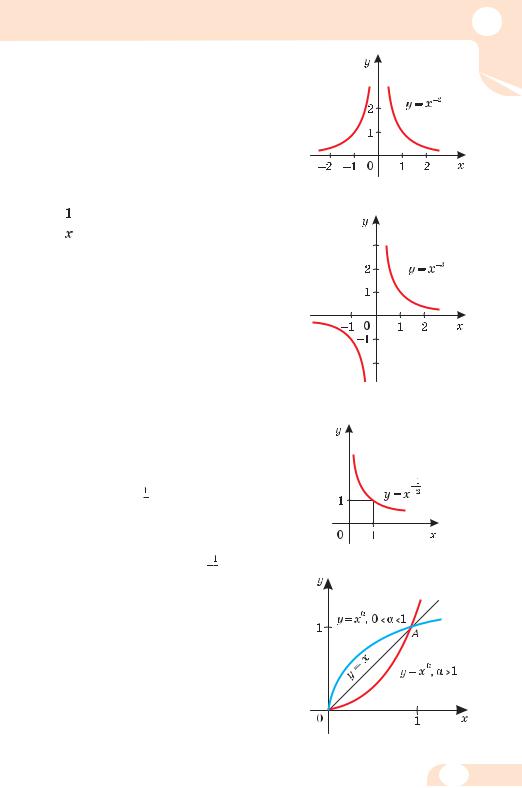
Властивості функції у = х2k, k N схожі з властивостями функції у = х2, а функції у = х2k+1, k N схожі з властивостями функції у = х3.

Якщо показник α степеневої функції – ціле від’ємне число, то вона визначена на множині всіх дійсних значень аргументу х, за винятком х = 0. Наприклад, функція у = х–1 – це вже відома вам обернена пропорційність

(див. мал. 28).

На малюнках 39 і 40 зображено графіки функцій у = х–2 і у = х–3.

Якщо α – від’ємне парне число, то графік функції у = хα симетричний відносно осі ординат, а якщо α – від’ємне непарне, то графік симетричний відносно початку координат. Узагалі, при кожному цілому показнику степеня α функція у = хα парна, якщо парне число α, і непарна при непарному α.

Якщо число α дробове, то степенева функція у = хα зазвичай розглядається лише на множині додатних значень аргументу, або на множині невід’ємних значень, якщо α > 0. Такою, зокрема,

є функція , яку можна записати

ще й так: (див. графік у табл., с. 34).

Графік функції 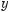зображено на малюнку 41.

Зверніть увагу на те, який вигляд має графік степеневої функції з додатним показником степеня α на проміжку [0; 1]. На цьому проміжку графіком функції у = хα (мал. 42) є:

1)відрізок ОА, якщо α = 1;

2)крива, направлена опуклістю вниз, якщо α > 1;

3)крива, направлена опуклістю вверх, якщо 0 < α < 1.

СТЕПЕНЕВІ ФУНКЦІЇ § 8

Мал. 39

Мал. 40

Мал. 41

Мал. 42

1 Ðîçäië

Чим більше додатне значення α, тим нижче від відрізка ОА розміщується графік функції у = хα.

На малюнку 43 схематично зображено співвідношення між деякими видами функцій. Цифрами 1, 2 і 3 позначено:

Мал. 43

1 – функція, яка водночас є лінійною і степеневою, – тільки одна: у = х.

2 – функція, яка водночас є квадратичною і степеневою, – тільки одна: у = х2.

3 – функція, яка водночас є і степеневою, і оберненою пропорційністю, також одна: у = х–1.

ПЕРЕВІРТЕ СЕБЕ

1.Сформулюйте означення степеневої функції з натуральним показником.

2.Які обмеження накладають на аргумент х функції у = хn, якщо n < 0?

3.Які види степеневої функції вам відомі?

4.Як розташовано на координатній площині графік функції у = хn, n N, якщо: а) n – непарне число; б) n – парне число?

1. Чи проходить графік функції у = x0,75 через точку М (16; 8)?

Розв’язання. Якщо х = 16, то у = 160,75 = 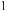= 8.

Відповідь. Проходить.

2. Що спільного і чим різняться графіки функцій

Розв’язання. – степенева функція з дробовим показником. Її область визначення D = [0; +∞). Графік міститься в І чверті (мал. 44).

СТЕПЕНЕВІ ФУНКЦІЇ § 8

Мал. 44

Мал. 45

Область визначення функції – множина всіх дійсних чисел R. Її графік міститься в І і ІІІ чвертях (мал. 45).

Для х 0 графіки функцій – однакові.

313.Наведіть приклади степеневих функцій.

314.Чи є степеневою функція, задана рівністю у = х?

315.Чи є степеневою функція, задана рівністю у = –х2?

316.Які з наведених функцій степеневі?

317.Чи правильно, що графік кожної степеневої функції проходить через точку (1; 1)?

318.Чи може графік степеневої функції проходити через початок координат? Якщо може, то наведіть приклад.

319.Чи є степеневою функція ? А функція у = (–х)–2?

320.Функція y = f(х) – степенева. Чи є степеневою функція:

а) y = –f(х); б) y = f(х) + 2; в) y = f(х) – 7; г) у = 2f(х)?

321. Обчисліть значення функції у точках: 0, 1, 8, 1000.

322. Побудуйте графік функції у = х2 на проміжку: а) [–3; 3]; б) [–2; 0]; в) [2; 3].

1Ðîçäië

323.Дано функцію у = х3 на проміжку [–2; 1]. Побудуйте її графік. Чи є дана функція парною або непарною?

324.Відомо, що функція у = х8 при х = с має значення m. Знайдіть значення цієї функції при х = –с.

325.Функція у = х7 при х = с має значення m. Знайдіть значення цієї функції при х = –с.

326.Доведіть, що графік кожної степеневої функції у = х2n проходить через точки А (1; 1) і В (–1; 1).

327.Чи проходить графік функції у = х0,25 через точку

М(16; 8)? А через М1(16; 2)?
328. Які з точок належать графіку функції: а) у = х2; б)
А (0,1; 0,01);	В (0,16; –0,4);	С (–10; 100);
329. Співставте властивості функцій у = (–х)2, у = –х2, у = х–2.
	Які з них степеневі? Побудуйте ескізи
	їхніх графіків.
	330. Користуючись графіком функ-
	ції у = х4 (мал. 46), знайдіть:
	а) значення функції, якщо значен-
	ня аргументу дорівнює: –1,6; –1,1;
	–0,9; 0,9; 1,4;
	б) значення аргументу, при якому
	значення функції дорівнює: 2; 3; 4;
	5; 6.
	331. За графіком функції у = х4
	(мал. 46) опишіть її властивості: яка
	область визначення цієї функції; на
	яких проміжках вона зростає; на
	яких спадає; при якому значенні х
	функція має найменше значення; чи
	має вона найбільше значення; чи є
	дана функція парною або непарною.
	332. За графіком функції у = х5
	(див. мал. 38) опишіть її властивості.
	333. Побудуйте графік функції:
	а) у = х4 + 1; б) у = х4 – 1.
	334. Відомо, що графік функції
	у = хα проходить через точку		.
	Знайдіть значення α.
	335. Функцію задано формулою
Мал. 46	у = хα. Знайдіть α, якщо графік
	функції проходить через точку:
68

		СТЕПЕНЕВІ ФУНКЦІЇ § 8
а) A(7; 49);	б) В(13; 169);	в) С(144; 12);
г) D(81; 9);	ґ) M(–64; –4);	д) N(–216; –6).

336.При якому значенні α графік функції у = хα проходить через точку ?

337.Знайдіть значення функції f(x) у точці х0, якщо

338.Порівняйте вирази, якщо α > 1:


	а) 0,15α і 0,34α;		б) 0,17α	і 0,23α;
	в) 3,1α і 4,52α;		г) 2,78α	і 6,9α.
339.	Побудуйте схематично графік функції:
	а) у = х–2;	б) у = х–2,5;		в) у = х–5.
340.	Розв’яжіть графічно рівняння:
	а) х4 = х;	б) х0,5 = 2 – х;		в) 2х5 = 3 – х.

341.

Порівняйте вирази, якщо 0 < q < 1:

а) 0,47q

і 0,51q;

б) 0,39q і 0,42q;

в) 3,14q

і 4,73q;

г) 9,2q і 11,38q.

342.

Функцію задано формулою у = хq. Знайдіть q, якщо

графік функції проходить через точку:

а) А(4; 0,5);

б) В(16; 0,25);

в)

343.

г)

ґ)

д)

Для поданих нижче функцій вкажіть нулі функції (як-

що такі є) та проміжки зростання чи спадання:

Побудуйте схематично графік функції (344, 345).

344.	а) у = х9 – 2;	б) у = х–7 + 1;	в) у = х–20 + 3.
345.	а) у = х–12 – 1;	б) у = х–0,9 + 2;	в) у = х–2,5 – 3.

346. Знайдіть значення функцій

у точці х = 3, коли відомо, що . Отримані дані запишіть у таблицю.

1 Ðîçäië

Яка з функцій має в точці 3 найбільше значення, а яка – найменше?

347. Знайдіть найбільше і найменше значення функцій

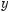
на проміжку [1; 9].

348. Запишіть рівняння степеневої функції у = f(х), якщо: а) f(–2) = 4, f(3) = 9; б) f(–1) = –1, f(2) = 8.

349.Співставте властивості функцій Заповніть відповідну таблицю.

350.Обчисліть значення виразу:

351.Якою цифрою закінчується число а = 1236 + 11112?

352.Морська вода містить 5 % солі. Скільки кілограмів прісної води треба додати до 40 кг морської води для того, щоб вміст солі в ній складав 2 %?

§ 9. Ірраціональні рівняння і нерівності

Рівняння називається ірраціональним, якщо воно містить змінні під знаком кореня або в основі степеня з дробовим показником.

Приклади ірраціональних рівнянь:

Деякі з таких рівнянь можна розв’язувати способом заміни.

Так, замінивши в першому рівнянні на у, дістанемо квадратне рівняння у2 – 5у + 4 = 0, корені якого у1 = 1, у2 = 4.

Отже, або , звідcи х1 = 1, х2 = 16.

Рівняння можна подати у вигляді (х – 1) + –

– 2 = 0, а потім, замінивши на у, звести його до квадратного.

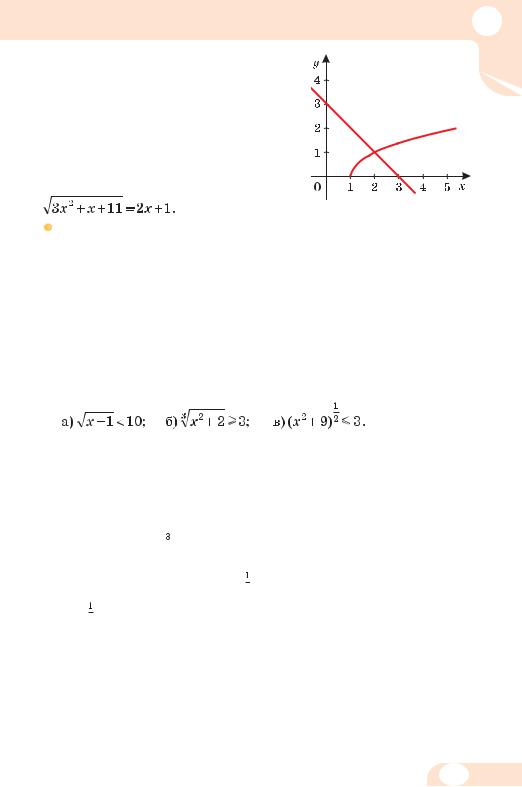
ІРРАЦІОНАЛЬНІ РІВНЯННЯ І НЕРІВНОСТІ § 9

Неважко розв’язати його і графічним способом (мал. 47). Отримаємо: х = 2.

Більшість ірраціональних рівнянь розв’язують піднесенням обох їх частин до степеня з тим самим натуральним показником. При цьому можуть з’явитися сторонні розв’язки, їх відкидають у результаті перевірки.

Прик лад. Розв’яжіть рівняння

Мал. 47

Р о з в ’ я з а н н я. Піднесемо обидві частини рівняння до квадрата:

3х2 + х + 11 = 4х2 + 4х + 1, або х2 + 3х – 10 = 0. Корені утвореного квадратного рівняння: –5 і 2.

Якщо х = –5, то якщо х = 2, то

Відповідь. х = 2.

Ірраціональною називають нерівність, яка містить змінну під знаком кореня або в основі степеня з дробовим показником.

Приклади:

Розв’язувати такі нерівності можна на основі властивостей відповідних степеневих функцій.

a) Оскільки функція зростає на всій множині невід’єм9 них чисел і , то нерівність рівносильна по9 двійній нерівності 0 х – 1 < 100, звідси 1 х < 101, х [1; 101).