
matametika_bevz_standart_1 / matametika_bevz_standart
.pdf
2 Ðîçäië
470. Знаючи, що sin α = , обчисліть значення cos α, tg α i ctg α за умови, що: 
а) 0 < α < ; б) < α < π.
471. Знаючи, що cos α = 0,8, обчисліть значення sin α, tg α i ctgα за умови, що:
а) 0 < α < ; б) – < α < 0.
472. Спростіть вираз:
а) sin2 α + соs2 α – tgαctgα; |
б) |
в) 1– (sinα + cosα)2; ґ) tgαctgα – соs2 α;
г) (1– sinα)(1 + sinα); д) sinα cosα ctgα.
473. Доведіть тотожність:
а) (1– sin2 α) tg2 α = sin2 α; б) (1– соsα)(1 + соsα) = sin2 α;
в) 1– sin2 α – соs2 α = 0; г) sin4 α + sin2 αсоs2 α + соs2 α = 1.
474. Доведіть тотожність:
а) sin4 α – соs4 α = sin2 α – соs2 α;
в) sin2 α – sin2 β = соs2 β – соs2 α;
Á
Доведіть тотожність (475–477).
475.a) 1 + sinα + соsα + tgα = (1 + соsα)(1 + tgα);
б) (sinα + tgα)(соsα + ctgα) = (1 + sinα)(1 + соsα).
476.a) sin3 α (1 + ctgα) + соs3 α (1 + tgα) = sinα + соsα; б) 3(sin4 α + соs4 α) – 2 (sin6 α + соs6 α) = 1.
477.






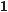





Спростіть вираз (478–480). |
|
|
|
|
|
|||||
478. |
а) 1 – соs2 α + sin2 α; |
б) 1 – sin2 α + sin2 αctg2 α; |
||||||||
|
в) (1 + tg2 α)соs2 α; |
г) (tgβ соsβ)2 + (ctgβsinβ)2. |
||||||||
479. |
а) (tgα + ctgα)соs2 α; |
б) 1 – sinβсоsβtgβ; |
||||||||
|
в) соs4 α + sin2 αсоs2 α; |
г) (tgϕ + ctgϕ)sinϕсоsϕ. |
||||||||
480. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
102

ФОРМУЛИ ЗВЕДЕННЯ §13
481. Знайдіть значення:
а) sinα, tgα, ctgα, якщо соsα = – і 90° < α < 180°;
б) соsα, tgα, ctgα, якщо sinα = –0,8 і 180° < α < 270°; в) sinα, соsα, ctgα, якщо tgα = –1 і 270° < α < 360°.
482.Побудуйте графік функції у = 4 – x2. При яких значеннях вона зростає, а при яких спадає? Знайдіть її нулі і найбільше значення.
483.Спростіть вираз:
484.Розв’яжіть рівняння:
§13. Формули зведення
Кожну тригонометричну функцію |
|
кутів ± α, π ± α, ± α, 2π ± α мож? |
|
на виразити через тригонометричну |
|
функцію кута α. Покажемо це спочат- |
|
ку для синусів і косинусів. |
|
Нехай α – довільний кут, вираже- |
|
ний у радіанах. На одиничному колі |
|
йому відповідає певна точка А, а куту |
|
– α – точка В (мал. 61). Опустивши |
Мал. 61 |
|
перпендикуляри АK на вісь х, ВL на
вісь у, дістанемо два рівних трикутники АОK і ВОL (оскільки
АОK = ВОL і ОА = ОВ). Тому ОL = ОK і ВL = АK, тобто
Кутам + α i – α на одиничному колі відповідають точки,
симетричні відносно осі у (мал. 62). Їх ординати рівні, абсциси протилежні. Тому
103
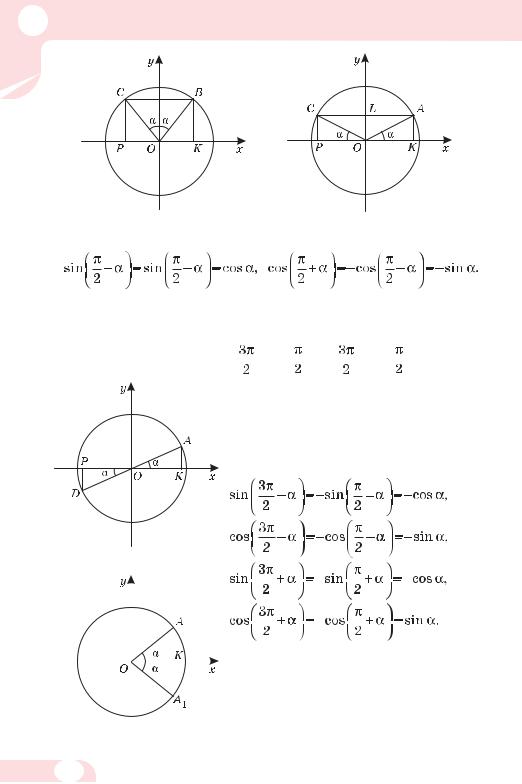
2 Ðîçäië
Мал. 62 |
Мал. 63 |
Кутам π – α і α також відповідають точки одиничного кола, симетричні відносно осі у (мал. 63). Тому
sin(π – α) = sinα, |
соs(π – α) = –соsα. |
|||||||
Кутам π + α і α (а також |
|
– α і |
|
– α, |
|
+ α і |
|
+ α) відпо? |
|
|
|||||||
|
|
|
||||||
відають точки одиничного кола, симетричні відносно початку координат (мал. 64). Їх ординати протилежні й абсциси також протилежні. Тому
sin(π + α) = –sinα, соs(π + α) = –соsα,
Мал. 64
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кутам 2π – α і α відповідають точ- |
||||||||||||
|
|
|
|
|
ки одиничного кола, симетричні |
||||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
відносно осі х (мал. 65). Їх абсциси |
||||||||||||
|
|
|
|
|
рівні, а ординати протилежні. Тому |
||||||||||||
|
|
|
|
|
|
|
|
sin(2π – α) = –sinα, |
|||||||||
Мал. 65 |
|
|
|
соs(2π – α) = соsα. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
104

ФОРМУЛИ ЗВЕДЕННЯ §13
Кутам 2π + α і α відповідає одна й та сама точка одиничного кола, тому
sin(2π + α) = sinα, соs(2π + α) = соsα.
З попередніх міркувань маємо 16 формул.
Ще 16 подібних формул можна довести для тангенса і котангенса:
Отже, 








Усі ці 32 формули називають формулами зведення, оскільки вони дають можливість кожну тригонометричну функцію довільного кута (а отже, і числа) звести до тригонометричної функції гострого кута. Запам’ятовувати кожну із цих формул немає потреби, краще користуватися загальним правилом.
Щоб зрозуміліше сформулювати правило, домовимося синус вважати кофункцією косинуса, і навпаки, а тангенс – кофункцією котангенса, і навпаки.
Говоритимемо також, що кут зводжуваної функції відкладається від горизонтального діаметра, якщо він має вигляд π ± α або 2π ± α, чи від вертикального діаметра, якщо він має вигляд
± α або ± α.
Правило зведення можна сформулювати так: якщо кут даної тригонометричної функції відкладається від вертикального діаметра, то її замінюють кофункцією, якщо ж – від горизонтального діаметра, то її назву не змінюють. Знак ставлять такий, який має значення даної функції за умови, що кут α гострий.
П р и к л а д. Нехай треба спростити вираз 





 . Перед
. Перед
результатом треба поставити знак мінус, оскільки коли кут α
гострий, то кут 

 належить ІІІ чверті і його косинус від’єм?
належить ІІІ чверті і його косинус від’єм?
ний. Кут |
|
– α відкладається від вертикального діаметра, |
|
тому назву функції соs треба замінити на sin. Отже,






 = –sinα.
= –sinα.
105

2 Ðîçäië
 Зауваження. Користуючися правилом зведення, ми тільки для зручності приймаємо, що кут α гострий. Насправді ж у кожній із формул зведення під змінною α можна розуміти й міру довільного кута, зокрема й від’ємного, і будь?яке дійсне число.
Зауваження. Користуючися правилом зведення, ми тільки для зручності приймаємо, що кут α гострий. Насправді ж у кожній із формул зведення під змінною α можна розуміти й міру довільного кута, зокрема й від’ємного, і будь?яке дійсне число.
 ПЕРЕВІРТЕ СЕБЕ
ПЕРЕВІРТЕ СЕБЕ
1.Що таке формули зведення?
2.Сформулюйте правило зведення.
3.Які знаки мають тригонометричні функції в кожній із чвертей?
4.Яку функцію називають кофункцією для синуса? А тангенса?
5. Чи може у формулі зведення α дорівнювати ? А 120°?
1. Доведіть тотожність:
 Р о з в ’ я з а н н я.
Р о з в ’ я з а н н я. 











2. Дану тригонометричну функцію зведіть до найменшого додатного аргументу:
а) sin845°; б) соs212°.
 Р о з в ’ я з а н н я. а) sin 845° = sin (360° 2 + 125°) = sin 125° = = sin(90° + 35°) = соs35°;
Р о з в ’ я з а н н я. а) sin 845° = sin (360° 2 + 125°) = sin 125° = = sin(90° + 35°) = соs35°;
б) соs212° = соs(180° + 32°) = –соs32°.
485. Які функції мають бути у порожніх клітинках таблиці?
Кути |
|
|
|
π – α π + α |
|
– α |
||
|
|
– α |
|
|
+ α |
|
||
|
|
|
|
|
||||
Функції |
|
|
|
|
|
|
||
sin |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
соs
tg
106
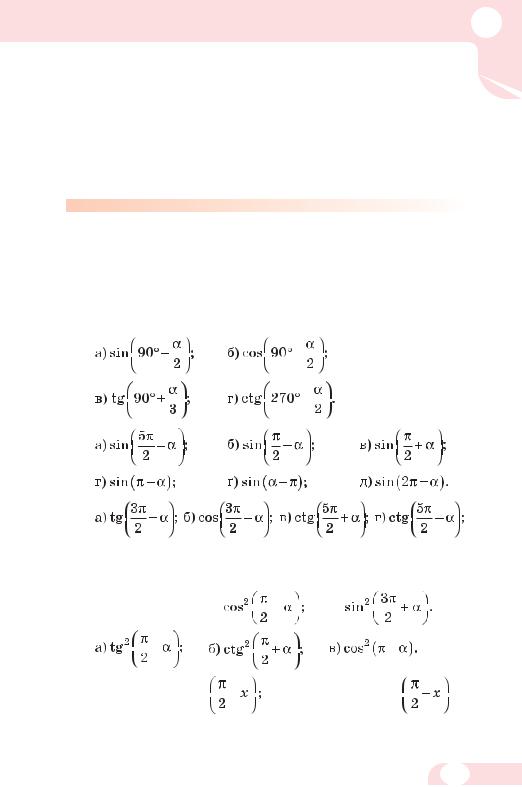
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ФОРМУЛИ ЗВЕДЕННЯ §13 |
|
486. |
Зведіть до найменшого додатного аргументу функції: |
|||||||||||||||||||||
|
|
а) sin94°; |
б) соs105°; |
|
|
|
в) tg192°; |
|||||||||||||||
|
|
г) соs269°; |
ґ) ctg179°; |
|
|
|
д) sin282°. |
|||||||||||||||
Спростіть вираз (487, 488). |
|
|
|
|
|
|
|
|
||||||||||||||
487. |
а) sin(90° + α); |
б) соs(90° + α); |
в) sin(α + 90°); |
|||||||||||||||||||
|
|
г) tg(90° + α); |
ґ) ctg(90° + α); |
д) tg(α + 180°). |
||||||||||||||||||
488. |
а) sin(180° – α); |
б) соs(180° – α); |
в) соs(α + 90°); |
|||||||||||||||||||
|
|
г) tg(180° – α); |
ґ) ctg(180° – α); |
д) ctg(α + 270°). |
||||||||||||||||||
À |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Спростіть вираз (489–494). |
|
|
|
|
|
|
|
|
||||||||||||||
489. |
а) sin(360° – α); |
б) tg(360° – α); |
|
|
||||||||||||||||||
|
|
в) соs(270° + α); |
г) tg(270° – α). |
|
|
|||||||||||||||||
490. |
а) sin(270° – α); |
б) соs(270° – α); |
|
|
||||||||||||||||||
|
|
в) соs(360° + α); |
г) ctg(360° – α). |
|
|
|||||||||||||||||
491. |
а) sin(90° – 2α); |
б) соs(90° + 3α); |
||||||||||||||||||||
|
|
в) tg(180° – 2х); |
г) ctg(180° + 3х). |
|||||||||||||||||||
492. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
493.
494.
ґ) tg(3π + α); д) cos(π + α); е) ctg(3π – α); є) соs(α + 5π).
Спростіть вираз (495–499). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
495. |
а) sin2(π + α); б) |
|
|
|
|
|
|
|
|
|
в) |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
496. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
497. |
а) sin(π – х) + sin |
|
|
|
|
|
|
|
|
|
|
|
б) соs(π + х) + cos |
|
|
|
|
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
498. |
а) sin(–α) + sinα; |
|
|
|
|
б) соsα + соs(–α); |
|
|
|||||||||||||||||||||||||
|
в) tg(–α) – tgα; |
|
|
|
|
г) ctgх + ctg(–х). |
|
|
|||||||||||||||||||||||||
107

2 Ðîçäië
499. |
а) sin(α – β) : sin(β – α); |
б) соs(х – α) : соs(α – х); |
||
|
в) tg(1 – α) : tg(α – 1); |
г) ctg(1 – 2х) : ctg(2х –1). |
||
Знайдіть значення виразу (500–502). |
|
|||
500. |
а) sin300°; |
б) соs240°; |
в) tg225°; |
г) ctg330°. |
501. |
a) sin(–210°); б) соs(–225°); |
в) tg(–240°); г) ctg(–315°). |
||
502. |
а) sin405°; |
б) соs720°; |
в) tg750°; |
г) ctg1110°. |
Á
Спростіть вираз (503, 504).
503.
504.
Знайдіть значення виразу (505–508). |
|
|||
505. |
а) соs810°; |
б) sin(–1470°); |
в) ctg1125°; |
г) tg1830°. |
506. а) ctg1500°; |
б) соs(–945°); |
в) соs3660°; |
г) sin1620°. |
|
507. |
а) соs450°; |
б) sin(–4095°); |
в) соs945°; |
г) tg1215°; |
|
ґ) sin585°; |
д) соs750°; |
е) tg(–9405°);є) sin1140°. |
|
508. |
а) sin3,5π; |
б) соs2,5π; |
в) tgπ; |
г) ctg1,75π. |
Зведіть функцію до найменшого додатного аргументу (509, 510).
509.
510.а) sin(3π + 2); б) соs(5π – 3); в) tg(0,5π + 1); г) сtg(π –4). Спростіть вираз (511–514).
511.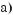




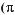

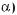


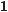








512. 

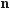



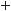

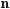
108

ВЛАСТИВОСТІ І ГРАФІКИ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ §14
513.
514.
Доведіть тотожність (515, 516).
515. 












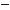


516.































517.Доведіть, що коли α, β, γ – кути трикутника, то:
518.У скільки разів і на скільки порядків число 4 107 більше за 8 106?
519.Розв’яжіть рівняння:
520.Які із функцій у = х2, у = –х, у = 0,5х3, у = 2х2 + 3, у =  парні, які – непарні?
парні, які – непарні?
§14. Властивості і графіки
тригонометричних функцій
Одна з найважливіших властивостей тригонометричних функцій в тому, що кожна з них – функція періодична.
Функцію у = f(x) називають періодичною, якщо існує таке дійсне число Т ≠ 0, що для всіх значень х із області її визначення
f(x – T) = f(x) = f(x + T).
Число Т називають періодом даної функції. Якщо Т – період деякої функції, то nТ, де n Z і n ≠ 0, також її період. Графік
109

2 Ðîçäië
Мал. 66
такої функції паралельним перенесенням уздовж осі х на Т, 2Т, ..., nТ одиниць вліво чи вправо відображається на себе (мал. 66).
Розглянемо спочатку конкретний приклад.
Функція у = sin х. Синус числа х – ордината точки одиничного кола, яка відповідає числу х (див. § 11). Оскільки кожному дійсному числу х відповідає єдине значення sin х, то у = sin х – функція, визначена на множині всіх дійсних чисел R. Щоб виявити найважливіші властивості цієї функції, побудуємо її графік. Спочатку – тільки на проміжку [0; 2π].
Складемо таблицю значень.
x |
0 |
|
|
|
π |
|
|
|
2π |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||
y |
0 |
|
1 |
|
0 |
–1 |
0 |
||
|
|
|
|
|
|
|
|
|
|
Точки з відповідними координатами нанесемо на координатну площину (мал. 67, а). Якщо обчислити значення sin х для всіх дійсних значень х і позначити на координатній площині всі відповідні їм точки, то дістанемо криву, зображену на малюнку 67, б. Це – графік функції у = sinх на [0; 2π].
На побудованому графіку показано, як змінюється ордината точки одиничного кола, здійснюючи о д и н повний обхід цього кола. На другому, третьому і наступних обходах усе повторюється. Це випливає також із тотожності sin(х + 2πn) = sin х. Тому, якщо криву, зображену на малюнку 67, б, перенести на кожний з проміжків [2nπ; 2(n + 1)π], де n – числа цілі, дістанемо весь графік (мал. 68).
а) |
б) |
Мал. 67
110
ВЛАСТИВОСТІ І ГРАФІКИ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ §14
Функція у = sin х періодична з найменшим додатним періодом 2π. Це видно на графіку функції (мал. 68). Можна міркувати й інакше. Оскільки завжди sin(х – 2π) = sinx = sin(х + 2π), то 2π – період функції у = sin х. А коли ця функція мала б додатний
період l < 2π, тоді правильною була б рівність 









 .
.
А за умови, що 0 < l < 2π, ця рівність неправильна (переконайтесь у цьому за допомогою одиничного кола). Отже, найменший додатний період функції у = sinх дорівнює 2π.
у = sin х
Мал. 68
Графік функції у = sinх – синусоїда (мал. 68); вона нескінченна в обидва боки. Розглянемо одну матеріальну модель синусоїди.
Якщо обгорнути свічку кілька разів папером, потім перерізати її гострим ножем під кутом 45° до осі свічки (мал. 69) і розгорнути папір, матимемо матеріальну модель частини синусоїди.
Мал. 69
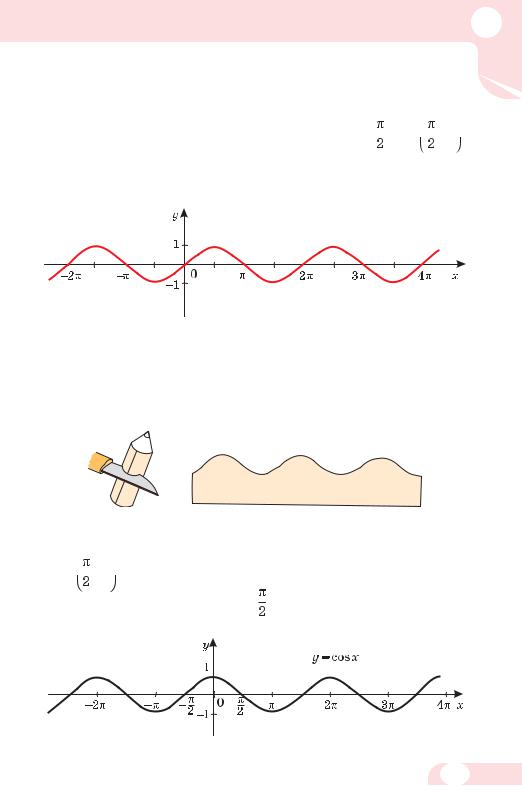
Оскільки для кожного значення х правильна рівність cosx =







 то графік функції у = соs х – така сама синусоїда,
то графік функції у = соs х – така сама синусоїда,
тільки зміщена вздовж осі х на одиниць уліво (мал. 70).
Мал. 70
111
