8Множення двійкових чисел

8.1 Методи множення бінарних чисел

Розглянемо основні способи виконання операції множення для різних систем. Найпоширенішим способом множення чисел є спосіб порозрядного множення множеного на множник, починаючи з молодшого розряду (1-й спосіб) і зі старшого розряду (2-й спосіб). Розглянемо приклад:

Аналіз способів множення чисел в десятковій системі показує, що операція множення складається з порозрядного множення множеного на множник з перенесенням переповнення в старший розряд, зрушення часткових добутків на один розряд вліво (вправо), підсумовування часткових добутків.

У двійковому численні це завдання значно спрощується, оскільки множити порозрядно немає необхідності. Насправді, якщо множити множене на "1", то це повторення множеного із зсувом на один розряд вправо (вліво), а на "0"  записуються одні нулі із зрушенням.

В обох випадках операція множення складається з ряду послідовних операцій зсуву і складання часткових добутків. Таким чином, операція множення зводиться до складання часткових добутків, які виходять з множеного або нулів, якщо в розряді множника «нуль», або множеного, якщо в розряді множника «одиниця» і відповідним зсувом.

Окрім операції складання, при виконанні множення, з’являється операція зсуву чисел. При цьому, можливі два варіанти:

- зсувати множене відповідно до вказівок множника;

- зсувати суму часткових добутків.

Розглянемо основні методи виконання операції множення ЦА.

8.2 Множення чисел з фіксованою крапкою (комою) на дспк

Запишемо машинне зображення множеного і множника у формі з фіксованою комою в прямому коді. A_np=Sg,α₁α_2...α_n; B_пр=Sg,b₁b₂...b_n. Тоді, їхній добуток запишеться як C_np=Sg,с₁с₂...с_n, де Sg_С=Sg_АSg_В, де   знак додавання функції «Σ mod2» (її ТІ: 1)

Таким чином, при використанні ДСПК, знак добутку визначається окремо від цифрової частини, потім виконується операція множення. Вона виконується відповідно до заданої структури множного пристрою (див. наприклад, рис. 7.1) і методу множення (див. наприклад, метод 2).

За методом 2 множення починається з молодшого розряду і зсувається вправо сума (Σ) часткових добутків.

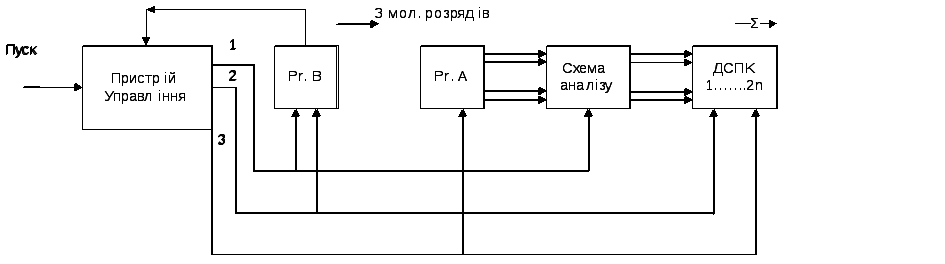Рисунок 8.1 Структура ЦА для пристрою множення чисел з фіксованою комою

Приклад. Помножити [А_пр]=11/11010 (26); [В_пр]=00/11001 (25), С= 650.

Рішення. Визначається знак добутку С: 10 =1.

Приймемо: а) суматор має 10 розрядів (без знака).

б) регістри мають по 5 розрядів (без знака).

Послідовність дій представимо таблицею 7.1

Для спрощення запису таблиць, приймемо наступні умовні позначки:

- оператор := привласнення значення (блоку ліворуч привласнюється значення, що є праворуч );

- позначення, наприклад, [См]  вміст суматора;

- операторзсуву вмісту, наприклад, регістра А вправо наодин розряд;

- позначення В. П.  вхідне положення;

-позначення А_пр, В_пр - цифрова частина множенного, множника (прямий код).

Відповідь: [С_пр]= 11/1010001010.

Таблиця 8.1Приклад рішення

Якщо при множенні виникає одиниця переносу зі старшого розряду, то її зберігають шляхом зсуву суматора (, тобто необхідно передбачати в ЦА стробування (фіксування) сигналу переповнення для виробу зсуву на один розряд вправо. Цей спосіб одержав найбільше поширення в практиці ЦА.