1.7. Трехфазные цепи

Трехфазной цепью называют совокупность трехфазного источника и трехфазного приемника, соединенных токопроводящими телами (ЛЭП).

Преимущества трехфазных цепей – простота и надежность, экономия металлических проводов при строительстве ЛЭП, возможность получения вращающегося магнитного поля, малые пульсации выпрямленного напряжения.

Симметричная трехфазная система ЭДС – это совокупность трех однофазных ЭДС, имеющих одинаковые частоты и амплитуды и сдвинутых по фазе друг относительно друга на 120°:

Основное свойство трехфазной симметричной ЭДС (или) доказывается путём графического сложения векторов (рис. 1.24,в).

а

Е_а

Рис. 1.24. Мгновенные значения трехфазной симметричной

системы ЭДС (а) и векторные диаграммы (б и в)

трехфазная симметричная ЭДС (комплексы).

1.7.1. Получение трехфазной симметричной системы эдс в промышленности

Т

Рис. 1.25. Устройство трехфазного

генератора: 1 – статор; 2 – ротор;

3 – обмотки статора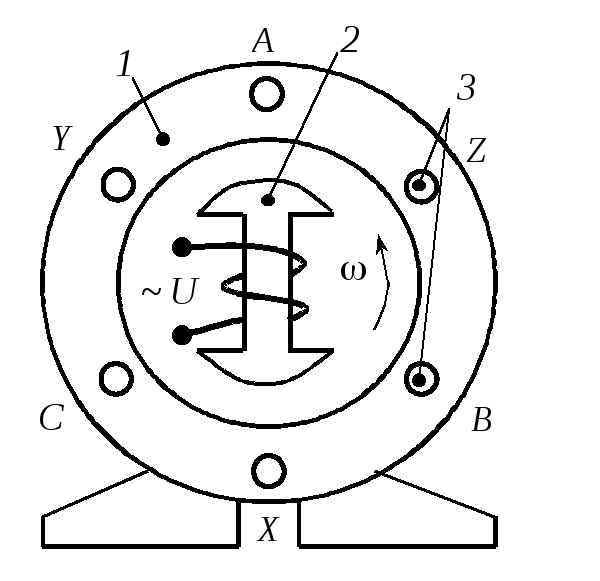

рёхфазную симметричную ЭДС получают с помощью трёхфазных синхронных генераторов (рис. 1.25). Для этого одинаковые обмотки в статоре располагают под углом 120°. При вращении ротора создаваемое им магнитное поле индуцирует в одинаковых обмотках одинаковые синусоидальные ЭДС. Сдвиг обмоток в пространстве обусловливает сдвиг синусоидальных ЭДС по фазе на угол 120°.

Под фазой в трехфазных цепях понимают обмотку генератора вместе с присоединенной к ней внешней цепью.

Нагрузка в трехфазных цепях бывает симметричной, если Z_a = Z_b = Z_c, и несимметричной.

Способы соединения источника и приемников в трехфазных цепях:

1. Соединение звездой с нулевым (нейтральным) проводом (четыре провода). Применяется при любой нагрузке.

2. Соединение звездой без нулевого провода (три провода). Применяется при симметричной нагрузке.

3. Соединение треугольником (три провода). Применяется при любой нагрузке.

1.7.2. Трехфазная цепь, соединенная звездой

В показанной на рис. 1.26 трехфазной цепи – вектор смещения нейтрали; N – нейтраль источника; n – нейтраль приемника.

Рис. 1.26. Трехфазная цепь при соединении источника

и приемников звездой

В трехфазных цепях различают фазные и линейные напряжения и токи.

Фазное напряжение – это напряжение между началом и концом фазы (– фазные напряжения источника;– фазные напряжения приемника).

Линейное напряжение – это напряжение между фазами. В цепи, соединенной по типу «звезда», фазный ток равен линейному (– линейные напряжения;– линейные (фазные) токи).

Связь между фазными U_ф и линейными U_л напряжениями. Анализируя схему по второму закону Кирхгофа, имеем

(3)

Из векторной диаграммы (рис. 1.27) имеем

Для источника это равенство справедливо всегда.

Рис. 1.27. Векторная диаграмма напряжений (а)

и соотношение между U_л и U_ф (б)

Связь между фазным напряжением источника и фазным напряжением приемника. Из второго закона Кирхгофа для схемы на рис. 1.26 имеем

(4)

Вектор смещения нейтрали делает систему напряжений на фазах приемника несимметричной (рис. 1.28).

Вектор смещения нейтрали определяем методом узлового напряжения:

(5)

где – проводимости соответствующих фаз приёмника и цепи нулевого провода.

Рис. 1.28. Векторная диаграмма

напряжений при

Случаи, когда вектор смещения нейтрали равен нулю:

а) при симметричной нагрузке

,

так как ;

б) при наличии нулевого провода

.

При симметричной нагрузке или при наличии нулевого провода (с ) , следовательно, система напряжений приемника совпадает с системой напряжений источника, и значит, она симметрична.

Только в этих случаях на нагрузке .

Токи в нагрузках определяются по закону Ома, а ток – по закону Кирхгофа:

(6)

При симметричной нагрузке токи образуют симметричную систему и , следовательно, нулевой провод не нужен.

Алгоритм расчета трехфазной цепи, соединённой звездой:

1. Определяем линейные или фазные напряжения источника (1).

2. По формуле (5) определяем напряжение .

3. По формулам (4) определяем напряжения на фазах приемника.

4. По формулам (6) определяем токи в фазах приемника и в нулевом проводе.

5. Строим векторную диаграмму.