88

Электрические цепи со взаимоиндукцией Напряжение на индуктивно связанных элементах цепи

Явление наведения ЭДС в одном элементе цепи при изменении тока в другом называют взаимоиндукцией. Про такие элементы говорят, что они индуктивно (или магнитно) связаны.

Пусть имеются две катушки (рис. 5.1.), по которым протекают токи и. В первой катушкевитков , во второй –. При этом эти катушки будут магнитно связаны так, как это показано на рисунке.

Здесь

	– магнитный поток, созданный током (поток самоиндукции первой катушки);
	– часть магнитного потока , связанная только с первой катушкой;
	– магнитный поток, созданный током (поток самоиндукции второй катушки);
	– часть магнитного потока , связанная только со второй катушкой;
	– поток взаимоиндукции – часть потока , которая связана со второй катушкой;
	– поток взаимоиндукции – часть потока , которая связана с первой катушкой.

Первую катушку пронизывает магнитный поток , вторую катушку –.

Потокосцепления первой и второй катушек соответственно равны

(5.1)

Здесь

–потокосцепление самоиндукции соответственно первой и второй катушек;

–потокосцепление взаимоиндукции соответственно первой и второй катушек;

Соотношения (5.1) справедливы только в том случае, когда потокосцепления самоиндукции и взаимной индукции совпадают по знаку. При изменении направления тока, например, во второй катушке, знаки перед потокосцеплениями взаимоиндукции должны измениться на противоположный. Поэтому формулы (5.1) можно переписать

(5.2)

при этом верхний знак в этих выражениях соответствует «согласному» включению катушек, а нижний – «встречному».

Опытным путем установлена связь между токами и потосцеплениями для катушек без ферромагнитных сердечников

(5.3)

В цепях, которые мы изучаем, . Здесь– индуктивность соответственно первой и второй катушек,M – взаимная индуктивность между катушками, измеряемая в Гн.

Степень магнитной (индуктивной) связи двух элементов цепи характеризуется коэффициентом связи K

(5.4)

т.к. , а, посколькуиявляются частью потокосцеплений соответственнои.

В соответствии с законом Фарадея-Ленца . Тогда напряжения на первой и второй катушках при изменении токаравны

(5.5)

Здесь

–напряжение самоиндукции;

–напряжение взаимоиндукции.

Одноименные зажимы катушек

Встречное и согласное включение индуктивно связанных элементов (катушек) зависит от направления тока в элементах и взаимного расположения катушек в пространстве.

Два зажима двух индуктивно (магнито) связанных элементов цепи называют одноименными, если при одном и том же направлении тока относительно этих зажимов потоки самоиндукции и взаимоиндукции на каждом элементе складываются. В электрических схемах такие зажимы обозначаются точками (·) или звездочками (*). Магнитная связь между элементами обозначается дугой со стрелками (рис. 5.2.).

Расчет гармонических цепей со взаимоиндукцией Последовательное соединение индуктивно связанных цепей

Рассмотрим расчет последовательной цепи со взаимоиндукцией на примере схеме, представленной на рис. 5.3., при согласном включении индуктивно связанных элементов.

–комплексное сопротивление первой реальной катушки индуктивности;

–комплексное сопротивление второй реальной катушки индуктивности.

Примечание: и– это сопротивления без учета магнитного влияния катушек друг на друга.

Уравнение по II закону Кирхгофа для мгновенных значений с учетом индуктивных связей имеет вид

(5.6.)

Здесь

–напряжение взаимоиндукции первой и второй катушек.

В комплексной форме это уравнение имеет вид

(5.7)

Здесь

–сопротивление взаимоиндукции;

–реактивное сопротивление при согласном включении;

–эквивалентная индуктивность при согласном включении магнитосвязанных элементов;

–напряжение на первой и второй катушках.

Из приведенных соотношений следует, что при согласном включении индуктивно связанных катушек их суммарное сопротивление больше, чем сумма сопротивлений этих катушек, не включенных по такой схеме.

Векторная диаграмма при согласном включении в соответствии с выражением (5.7.) имеет вид, представленный на рис. 5.4.

На рис. 5.5 представлено встречное включение индуктивно связанных катушек. Для этой схемы справедливо

Или в комплексной форме

При этом эквивалентная индуктивность и эквивалентное сопротивлениепри встречном включении

(5.9)

При встречном включении индуктивно связанных катушек их суммарное сопротивление меньше, чем сумма сопротивлений этих катушек, не включенных по такой схеме.

Векторная диаграмма при встречном включении имеет вид, как на рис. 5.6.

При встречном включении может наблюдаться режим, при котором ток на одной из катушек опережает напряжение . Это может иметь место в случае, если напряжение самоиндукции первой катушки. При этом говорят, что в этой цепи наблюдается емкостный эффект. Векторная диаграмма при этом имеет вид, представленный на рис. 5.7.

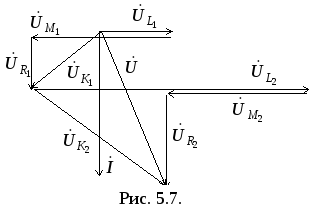
Напряжение первой катушки отстает от тока, т.е. наблюдается емкостный эффект. Однако следует отметить, что напряжениеучастка цепи с двумя индуктивно связанными последовательно включенными элементами всегда опережает ток, т.е. такая цепь носит индуктивный характер. Покажем это. Очевидно, что

. Отсюда следует, что . Но из соотношения для коэффициента магнитной связи, следовательно,, аи. Из приведенных соотношений следует справедливость утверждения: цепь с двумя последовательными индуктивно связанными элементами всегда носит индуктивный характер.