Последовательное соединение r, l, c

Для мгновенных значений токов и напряжений выполняются I и II законы Кирхгофа.

При прохождении синусоидального тока через электрическую цепь, состоящую из последовательно соединенных элементовR, L, C (рис. 3.9.), на выводах a-b этой цепи создается синусоидальное напряжение, равное по II закону Кирхгофа алгебраической сумме синусоидальных напряжений на отдельных элементах:

(3.21)

Из тригонометрии известно, что

. (3.22)

Применим формулу (3.22) к выражению (3.21):

(3.23)

–реактивное сопротивление последовательной RLC - цепи, которое может принимать следующие значения:

–цепь носит чисто активный характер (в цепи резонанс);

–цепь носит индуктивный характер, т.е. ;

–цепь носит емкостный характер, т.е. .

–полное сопротивление цепи;

–угол разности фаз определяется по оси от кривой напряжения к кривой тока и бывает острым или прямым:j < 0 при емкостном характере цепи (ток опережает напряжение), j > 0 при индуктивном характере цепи (ток отстает по фазе от напряжения), j = 0 при резистивном характере цепи (индуктивное и емкостное сопротивления равны) – такой режим цепи называют резонансом напряжений.

Из выражений иследует, что связь активного и реактивного сопротивления с полным сопротивлением выражается следующими формулами:

, (3.24)

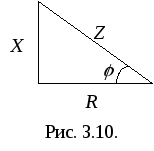
что удобно представлять с помощью треугольника сопротивлений (рис. 3.10.).

Умножив левые и правые части выражений для сопротивлений (3.23) на действующее значение тока I, получим соответственно действующие значения напряжений на активном и реактивном сопротивлениях, которые называют активной и реактивной составляющими напряжения:

(3.25)

Тогда действующее значение суммарного напряжения можно определить как Для напряжений также можно построить прямоугольный треугольник напряжений.

Параллельное соединение r, l, c

Если к выводам электрической цепи, состоящей из параллельно соединенных R, L, C (рис. 3.11.), приложено синусоидальное напряжение то поI закону Кирхгофа синусоидальный ток в неразветвленной части равен алгебраической сумме синусоидальных токов в параллельных ветвях

где

–совпадает по фазе с напряжением u(t)

–отстает по фазе от напряжения u(t) на .

–опережает по фазе напряжение u(t) на .

Просуммируем:

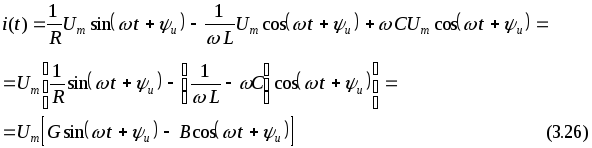
выражение (3.25) является тригонометрической формой записи I закона Кирхгофа для мгновенных значений.

–активная проводимость цепи, всегда положительна;

–реактивная проводимость цепи, которая в зависимости от знака может иметь индуктивный (В > 0) или емкостный (B < 0) характер. Если В = 0, цепь носит активный характер.

Для нахождения иj воспользуемся приемом, приведенном в предыдущем разделе:

, (3.27)

т.е. ток отстает от напряжения на угол j.

–начальная фаза напряжения;

–начальная фаза тока;

–разность фаз;

–амплитудное значение тока;

–полная проводимость цепи – величина, обратная полному сопротивлению ;

–угол разности фаз определяется по оси в направлении от напряжения к току и является острым или прямым .

–при индуктивном характере цепи, т.е. при B > 0; при этом ток опережает по фазе напряжение.

–при емкостном характере цепи, т.е. при B < 0; при этом ток опережает по фазе напряжение.

–при резистивном характере цепи, т.е. при равенстве индуктивной и емкостной проводимостей ; при этом ток совпадает по фазе с напряжением. Такой режим работы электрической цепи называютрезонансом токов.

Активная и реактивная проводимости цепи связаны с полной проводимостью формулами:

(3.28)

Для проводимостей также можно построить треугольник проводимостей.

Активная и реактивная составляющие тока определяются следующим образом:

(3.29)

Активная и реактивная составляющие тока связаны с действующим значением суммарного тока формулой . Для токов также можно построить треугольник токов.

Следует отметить, что описывать электрические цепи синусоидального тока, оперируя понятиями мгновенного значения тока и напряжения, достаточно трудоемко и применимо только для простейших электрических цепей, не содержащих большого числа контуров и источников. С усложнением электрических цепей такая форма расчета становится крайне затруднительной и требуется метод, позволяющий рассчитывать электрические цепи переменного тока алгебраически аналогично цепям постоянного тока. Таким удобным расчетным методом служит символический метод.