46 Общий случай расчета цепи первого порядка.

Дано: RL, RC, источник тока, ЭДС.

Алгоритм расчета:

1) Расчет до коммутационной цепи(ключ не сработал)

Замена при постоянном источнике: L- К.З.

С- обрыв

Расчет независимых нач. усл.:

- если есть в цепи ёмкость

Расчет любым известным методом

2) Расчет принужденной составляющей по виду Эл-ой цепи в новом стационарном режиме (ключ сработал)

3) Определение корня хар-го уравнения:

3.1 с помощью выводного диф. Ур.(ч\з закон Кирхгофа)

3.2 метод входного сопротивления(входной прводимости)

3.3 при помощи главного определителя

3.4 ч\з постоянную времени: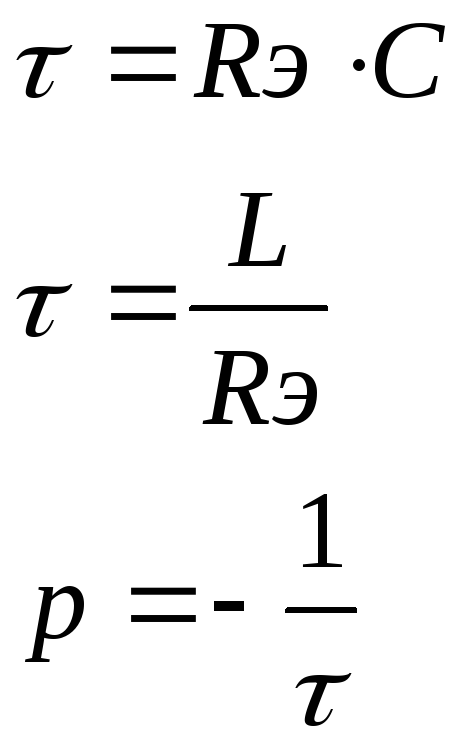

4)запись свободной составляющей:

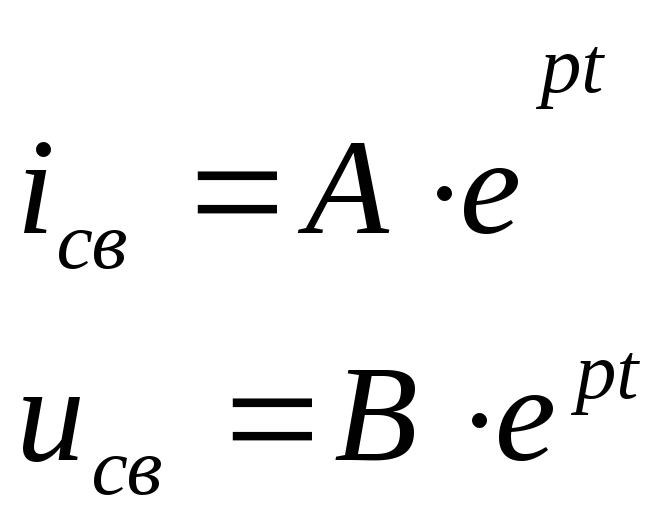
5)запись полного решения:

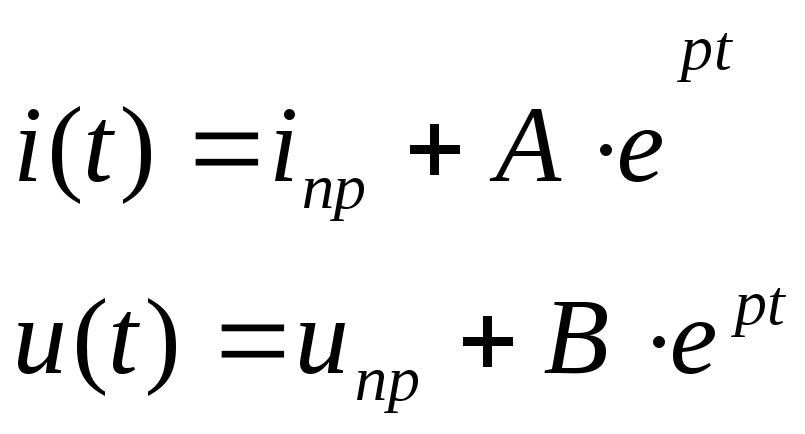
6)Определение постоянной интегрирования:

6.1 С помощью сист.диф. Ур. В (0+) дополненную независимыми нач. усл.(П 1)

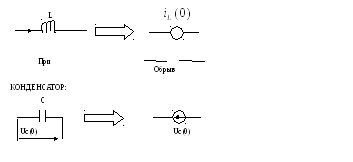
6.2 с помощью сх. Замещения в (0+):

Схемы замещения:

В t= (0+)

E= const

J=const

ЁМКОСТЬ

7) получение окончательного решения

8) график

Неоднородная цепь

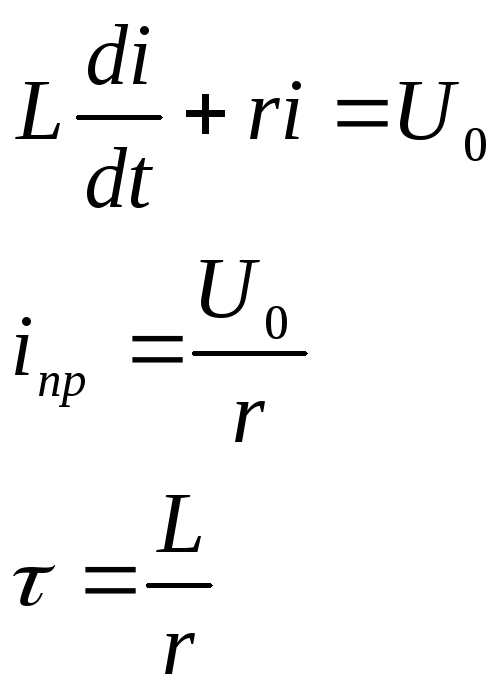
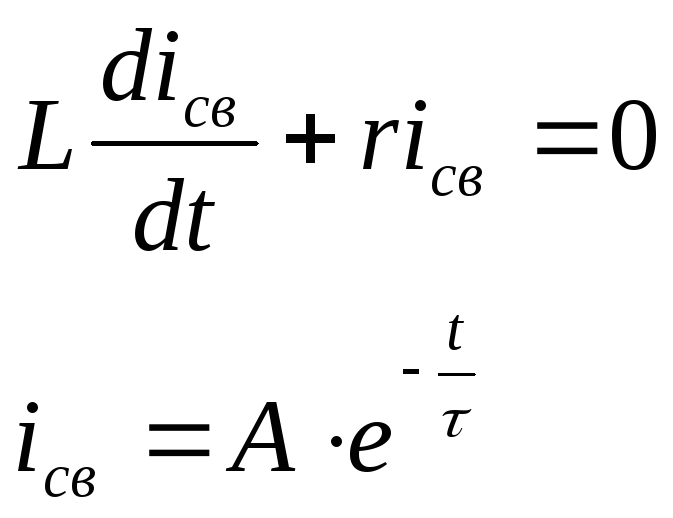
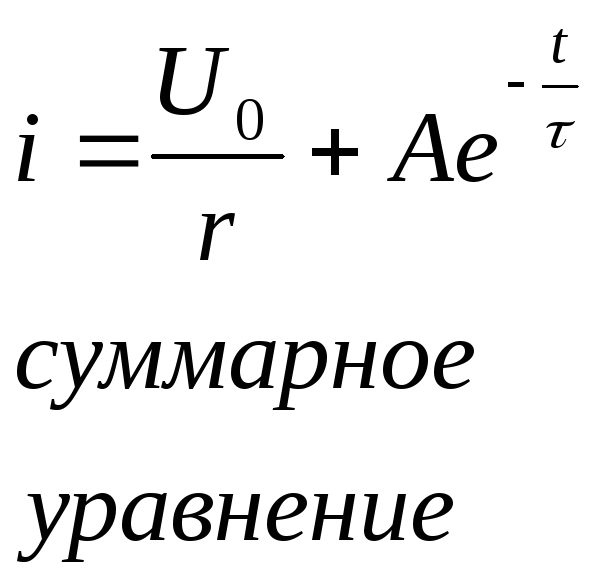
t=0 в начальный момент времени

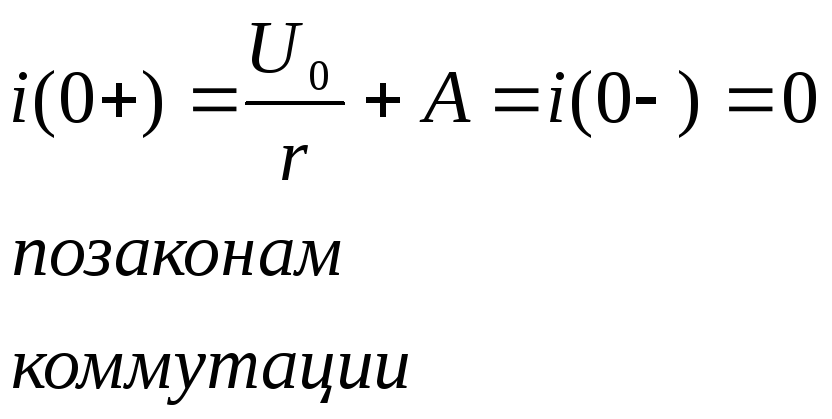
А=-,- закон изменения переходного тока

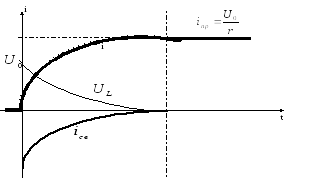
ВРЕМЕННАЯ ДИАГРАММА:

Законы Ома и Кирхгофа в операторной форме

Р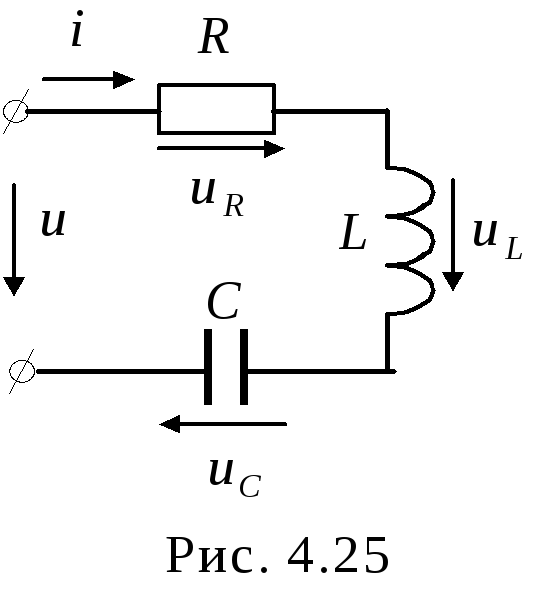ассмотрим цепь (рис. 4.25).II закон Кирхгофа во временной области (для оригиналов):

. (4.29)

К уравнению (4.29) применим преобразование Лапласа. Преобразование Лапласа является линейным, поэтому изображение суммы равно сумме изображений:

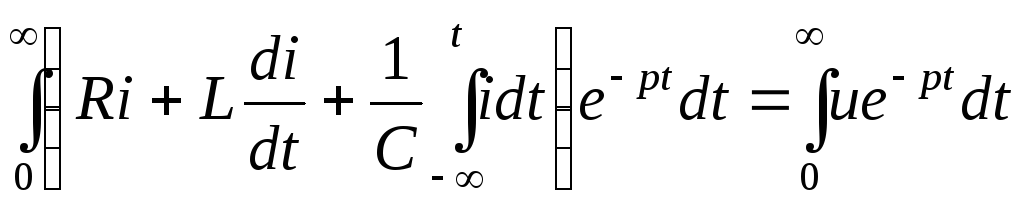. (4.30)

Каждое слагаемое уравнения (4.30) заменим операторным изображением:

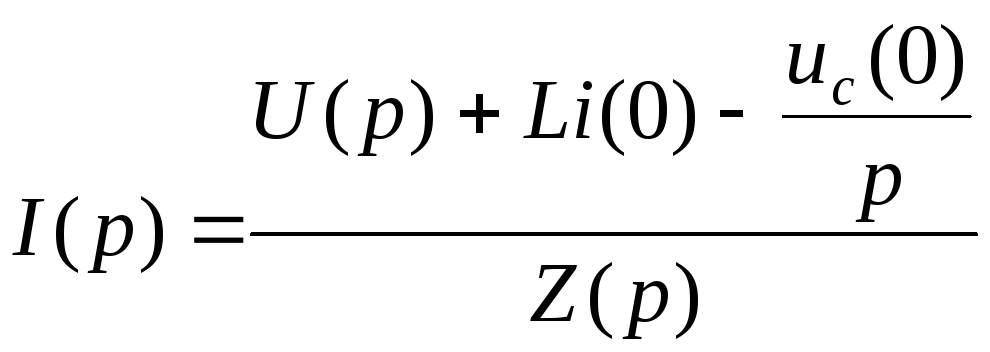, (4.31)

где – операторное сопротивление;

– операторная ЭДС, учитывающая ненулевой запас энергии магнитного поляW_м в индуктивности (по току i_L(0));

– операторная ЭДС, учитывающая ненулевой запас энергии электрического поляW_эл в емкости (по напряжению u_C(0))/

При нулевых начальных условиях (аналогично цепям постоянного тока).

По I закону Кирхгофа, алгебраическая сумма мгновенных значений токов, сходящихся в любом узле схемы, равна нулю . Применим преобразование Лапласа к этому уравнению и воспользуемся тем, что изображение суммы равно сумме изображений

.

(4.32)Уравнение (4.32) выражает собой I закон Кирхгофа в операторной форме, аналогично выражению для цепей постоянного тока.

Для любого замкнутого контура электрической цепи можно составить уравнение по II закону Кирхгофа . Применим преобразование Лапласа

. (4.33)

Уравнение (4.33) представляет собой математическую запись II закона Кирхгофа в операторной форме, уравнение (4.34) представляет собой модификацию (4.33)

. (4.34)

Аналог в цепях постоянного тока .

При нулевых начальных условиях просматривается полная аналогия с цепями постоянного тока, при ненулевых появляются отличия, заключающиеся в необходимости введения операторных ЭДС, учитывающих и отображающих ненулевой запас энергии магнитного поля W_м в индуктивности и энергии электрического поля W_эл в емкости.

Отсюда важный вывод: весь расчетный аппарат работает и при анализе переходных процессов, только в операторной форме. При этом необходимо учесть операторные ЭДС.

Замыкание катушки (RL) наR

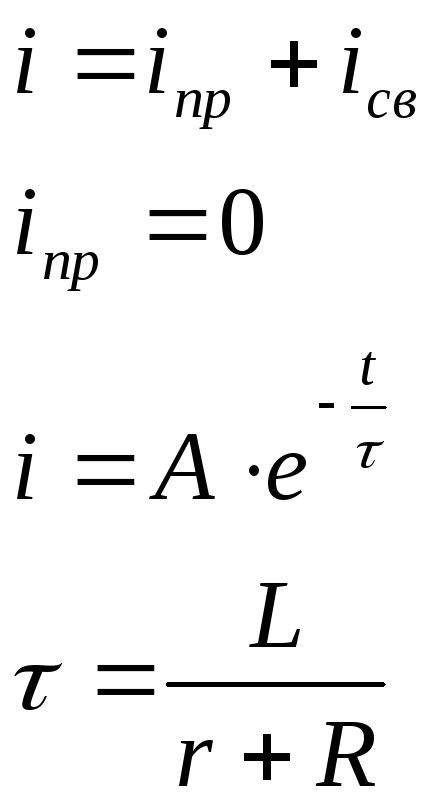
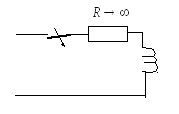
Напряжение растет до бесконечности, такого не может быть!!!