
- •4.3. Основні теоретичні відомості 33
- •5.3. Основні теоретичні відомості 41
- •Зміст та оформлення лабораторних робіт
- •Лабораторна робота №1
- •1.4 Індивідуальні завдання до лабораторної роботи
- •1.5 Контрольні питання
- •2.3.2 Побудова емпіричної формули
- •2.3.3 Вибір ступеня многочлена
- •2.4 Індивідуальні завдання до лабораторної роботи
- •2.5 Контрольні питання
- •3.3 Короткі теоретичні відомості
- •3.3.1 Чисельне диференціювання функцій
- •3.3.2 Метод Рунге збільшення порядку точності формул
- •3.3.3 Функції matlab для чисельного диференціювання
- •3.4 Індивідуальне завдання до лабораторної роботи
- •3.5 Контрольні питання
- •4.3 Основні теоретичні відомості
- •Обчислення визначених інтегралів в системі MatLab
- •4.4 Індивідуальні завдання до лабораторної роботи
- •4.5 Контрольні питання
- •5.3.2 Метод Ейлера
- •5.3.3 Методи Рунге-Кутта
- •5.3.4 Рішення задачі Коші в MatLab
- •5.4 Індивідуальні завдання до лабораторної роботи
- •5.5 Контрольні питання
- •Список літератури
2.3.2 Побудова емпіричної формули
Побудова емпіричної формули складається з двох етапів:
підбір загального вигляду формули;
визначення найкращих значень параметрів, що містяться у формулі.
Іноді загальний вигляд формули відомий з фізичних або інших міркувань. У інших випадках вигляд може бути довільним, перевага віддається найбільш простим формулам, які можуть вибиратися з геометричних міркувань, після нанесення експериментальних точок на координатну площину і порівняння отриманої кривої з графіками відомих функцій.
Підбір загального вигляду емпіричної формули
Проста емпірична формула
![]() .
.
Про
застосовність цієї формули можна судити
по величинах
![]() .
Якщо ki
.
Якщо ki
![]() const
, то формула може бути застосована.
const
, то формула може бути застосована.
У ряді випадків до лінійної залежності можуть бути зведені експериментальні дані, коли їх графік в декартовій системі координат не є прямою. Це може бути досягнуто шляхом введення нових змінних : u=φ(x,y), v=z(x,y), які вибираються так, щоб точки ui, vi лежали на прямій. Таке перетворення називається вирівнюванням(лінеаризацією) даних, в результаті отримуємо лінійну залежність u=a v + b.
Наприклад, ступенева залежність y=c•xA, логарифмуванням перетворюється до виду:
ln(y) = A ln(x) + ln(c).
Зробивши заміну змінних і постійної
X=ln(x), Y=ln(y), b=ln(c)
перейдемо до лінійної залежності
Y=A X + b.
Іншою простою емпіричною формулою є квадратний тричлен:
y = ax2 + bx + c.
В загальному випадку, коли ми нічого не знаємо про фізичний характер шуканої залежності, можна використовувати поліном ступеня m:
y = a0 + a1x + a2x2+ … + amxm.
Визначення параметрів емпіричної залежності методом найменших квадратів
Вважатимемо, що тип емпіричної формули вибраний і її можна представити у виді
y = g(x, a0, a1, ..., am),
де g - відома функція, a0, a1, …, am - невідомі постійні параметри. Завдання полягає в тому, щоб визначити такі значення цих параметрів, при яких емпірична формула дає добре наближення данної функції, значення якої в точках xi дорівнює yi (i=1, 2,…, n) (таблиця.2.1).
Позначимо через εi відхилення - різниця між значеннями емпіричної формули і функції, яку необхідно визначити, у вузлах xi. Тоді
εi = g(x, a0, a1, …, am) - yi, i=0, 1, … , n.
Задача знаходження найкращих значень параметрів a0, a1, …, am зводиться до деякої мінімізації відхилень εi. Існує декілька способів рішення цієї задачі. Ми зупинимося на одному - методі найменших квадратів : застосування критерію найменших квадратів призводить до визначення параметрів, які необхідно визначити, з умови мінімуму суми квадратів відхилень:
![]() .
.
Використовуючи необхідну умову екстремуму,
![]() ,
k=0,1,
…,m,
,
k=0,1,
…,m,
отримуємо так звану нормальну систему методу найменших квадратів :
![]() ,
k=0,1, …, m.
,
k=0,1, …, m.
Отримана система - є система алгебраїчних рівнянь відносно невідомих a0, a1, ., am . Можна показати, що визначник цієї системи відмінний від нуля, тобто рішення існує і єдино. Проте при високих ступінях m система є погано обумовленою. Тому метод найменших квадратів застосовують для знаходження многочленів, ступінь яких не вище 5. Рішення отриманої системи можна знайти, наприклад, методом Гауса.
Запишемо
нормальну систему найменших квадратів
для двох простих випадків: m=0 і m=2. При
m=0 емпірична формула набере вигляду:
g(x)=a0.
Для знаходження невідомого коефіцієнта
a0
маємо рівняння:![]() .Отримуємо, що
коефіцієнт є середнє арифметичне
значень функції в заданих точках.
.Отримуємо, що
коефіцієнт є середнє арифметичне
значень функції в заданих точках.
Якщо
ж використовується многочлен другого
ступіня
![]() ,
те нормальна
система рівнянь набере вигляду:
,
те нормальна
система рівнянь набере вигляду:

Вирішуючи цю систему лінійних рівнянь, отримуємо коефіцієнти a0, a1, …, am , многочлена, які є параметрами емпіричної формули, що необхідно визначити.
![]()
Отриману систему можна записати в компактнішому виді зручному для програмування:
c00a0 + c01a1 + … + c0mam = b0,
c10a0 + c11a1 + … + c1mam = b0,
………………………………
cm0a0 + cm1a1 + … + cmmam = b0,
де
ckl = ∑xik+l, bk = ∑xikyi, k,l = 0, 1, … , m.
Приклад 2.3.1 Нехай функція задана таблицею своїх значень :
|
x |
-3 |
-1 |
0 |
1 |
3 |
|
y |
-4 |
-0.8 |
3.6 |
4.3 |
3.5 |
Наблизимо функцію многочленом 2-ого ступіня. Для цього обчислимо коефіцієнти нормальної системи рівнянь:
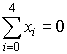 ,
,
 ,
,
 ,
,
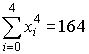
 ,
,
 ,
,

Складемо нормальну систему найменших квадратів, яка має вигляд:
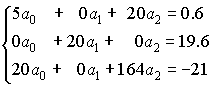
Рішення системи легко знаходиться: будь-яким з відомих методів, отримаємо:
a0 =3.234, a1 = 0.98, a2 = -0.278.
Таким чином, емпірична формула має вигляд:
g(x) =3.234 + 0.98x – 0,279x2
