1.1.2 Елементи векторної алгебри.

Координати вектора визначаються формулою ,якщо задані точки і .

Вектори і можна додавати і віднімати , де і довільні сталі. Якщо вектори лінійно незалежні, то вони утворюють базис і вектор може бути розкладений по цьому базису: , де – деякі числа. Якщо вектори іколінеарні, то їх координати пропорційні:.

Скалярний добуток векторів івизначається (, де- кут між векторамиі. Якщо вектори задані координатами, то скалярний добуток (. Умова перпендикулярності векторів: (0. Довжина вектора:. Кут між векторамиі:. Проекція векторана вектор: . Робота сили , яка прямолінійно переміщує матеріальну точку з початку в кінець векторавизначається формулою.

Векторним добутком векторів іє вектор, що задовольняє умовам: а) вектор б) довжина вектора обчислюється за формулою:, де- кут між векторамиі; в) утворюють праву трійку. Якщо вектори задані координатами, то векторний добуток обчислюється як . Площа трикутника АВС, для якого задані координати вершин, обчислюється як. Момент сили, прикладеної в точці, відносно точки визначається векторним добутком .

Мішаний добуток трьох векторів - це векторно-скалярний добуток 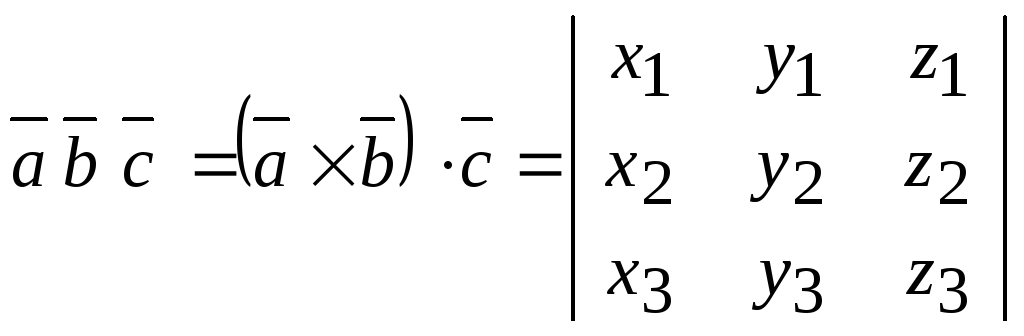, де . Три вектори компланарні, якщо вони належать одній площині або паралельним площинам. Умова компланарності трьох векторів: . Модуль мішаного добутку векторів дорівнює об’єму паралелепіпеда, побудованого на цих векторах. Об’єм піраміди . Знак вибираємо таким чином, щоб об’єм був додатним.

Задача 5. Перевірити колінеарність векторів, побудованих на векторах і, якщо .

Розв’язання: Знайдемо координати векторів :

.

Перевіримо умову колінеарності векторів:

Вектори не колінеарні, так як їх координати не пропорційні.

Задача 6. Задані координати вершин піраміди . Знайти:

а) Кут між ребрами та ; б) Площу грані ; в) Проекцію вектора на вектор, г) Довжину висоти піраміди, проведену з вершини , д) Яку трійку утворюють вектори , і ?

Дано: , , , .

Розв’язання:

Знайдемо координати векторів, на яких побудована піраміда: ,,.

а) Тоді косинус кута між ребрами та :

. Маємо

б) Площу грані знайдемо, як половину модуля векторного добутку векторів та :

.

=

(кв.од.)

в) Проекцію на обчислюємо за формулою:

г) Об^’єм піраміди обчислимо, застосовуючи мішаний добуток векторів , і .

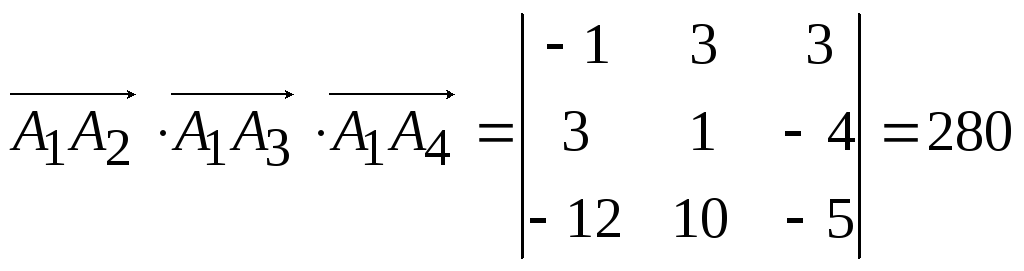, (куб.од.)

Для знаходження висоти піраміди застосовуємо формулу

кв.од. і куб.од. Підставимо i в формулу для обчислення висоти:

(лін.од.)

д)Так як мішаний добуток векторів , то вони утворюють праву трійку.

Задача 7. Визначити при якому значенні  вектори i взаємно перпендикулярні.

Розв’язання: Запишемо вектори в координатній формі: .Знайдемо скалярний добуток цих векторів: .З умови перпендикулярності векторів: маємо

.

Задача 8. З^’ясувати, чи належать чотири точки , , і одній площині.

Розв’язання: Якщо 4 точки лежать в одній площині, то вектори ,, належать цій площині, отже будуть компланарні.

Перевіримо це. Знайдемо координати цих векторів: , і їх мішаний добуток

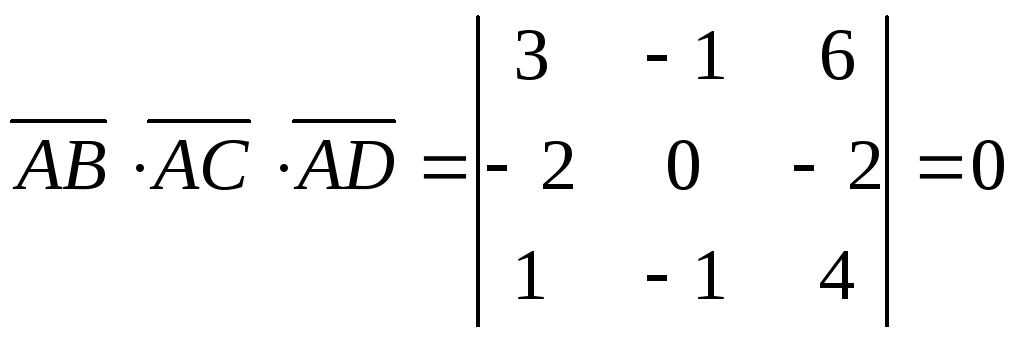
Вектори компланарні, точки А, В, С, D лежать в одній площині.

Задача 9. Дані сила = (5;−1;2) і дві точки і . Треба знайти: а) Роботу сили , необхідну для переміщення тіла із точки в точку ; б) Момент сили відносно точки, якщо сила прикладена в точку .

Розв’язання:

а) Робота А сили визначається як скалярний добуток сили на вектор переміщення. Знайдемо координати вектора:

= (0 − 3; 2 − (−1); −2 −1) = (− 3; 3;−3)

Тоді = ( 5; –1; 2 )( –3; 3; –3) = 5 (–3) + (–1)3 + 2(–3) = = –15 –3 –6 = –24.

б) Момент силивідносно точки, якщо сила прикладена в точку визначається як векторний добуток сили на плече.

.