2 Контрприклади у темі ”диференціювання”

Має місце теорема. Якщо функція диференційовна в точці, то вона неперервна в цій точці.

Доведемо її. Оскільки функція диференційовна в точці, то існує кінцева границя

.

Тоді за теоремою про зв’язок нескінченно малої з функцією, яка має кінцеву границю, будемо мати

,

де - нескінченно мала величина при.

Звідки

.

Переходячи в цій формулі до границі при , отримаємо згідно властивостей нескінченно малих, що

.

Отже, функція в точціє неперервною.

Обратна теорема не є вірною, тобто функція може бути неперервною в даній точці, але не бути диференційовною в цій точці.

Функція sgn(x) визначається наступним чином:

.

Контрприклад 1 (Приклад 3).

Розривна функція, яка всюди має похідну, (не обов̕язково кінцеву).

Для того, щоб такий приклад став можливий, потрібно розширити визначення похідної так, щоб воно включало значення ±∞. Тоді розривна функція має похідну

.

Ми переконалися, що функція всюди має похідну, але є розривною.

Окіл точки – це множина, яка містить дану точку та близькі до неї.

Теорема Дарбу. Точки, в яких похідна функції дорівнює 0 або не існує, поділяють область визначення функції на проміжки, усередині яких похідна зберігає знак.

Контрприклад 2 (Приклад 4).

Диференційовна функція, похідна якої не зберігає знака в жодному односторонньому околі екстремальної точки.

Функція:

Маємо абсолютний мінімум в точці . А її похідна:

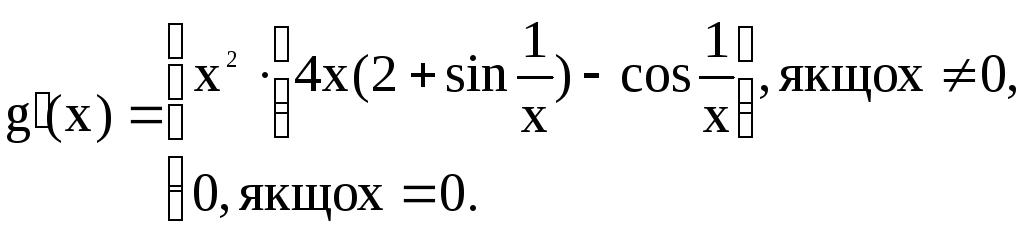
У будь якому околі нуля похідна має як додатнє, так і від’ємне значення. Функція не є монотонною ні в якому односторонньому околі точки .

Не зростаючі та не спадаючі функції називаються монотонними.

Функція строго зростаюча або строго спадна на проміжку називається строго монотонною на цьому проміжку.

Теорема. Якщо похідна функції на деякому проміжку Х, то функціязростає на цьому проміжку, якщо жна проміжку Х, то функціяспадає на цьому проміжку.[2]

Приклад. Дослідити функцію на монотонність на всій числовій прямій.

Знайдемо похідну заданої функції:

.

Для будь якого дійсного :, а тому робимо висновок, що задана функція зростає на всій дійсній осі.

Контрприклад 3 (Приклад 5).

Диференційовна функція, похідна якої додатня у деякій точці, але сама функція не монотонна ні в якому околі цієї точки.

Функція

має похідну, рівну:

У будь якому околі нуля похідна має як додатнє, так і від’ємне значення.

Як зазначалось раніше, функція може бути неперервною в даній точці, але не бути диференційовною в цій точці.

Контрприклад 4 (Приклад 8).

Всюди неперервна, але ніде не диференційовна функція. Функція всюди неперервна, але не диференційовна в точці х=0. Дослідимо функцію в точці, яка неперервна в точці(так як і в інших точках числової прямої). В цій точці її лівостороння та правостороння границі дорівнюють нулю, що співпадає зі значенням самої функції в точці 0. За означенням

.

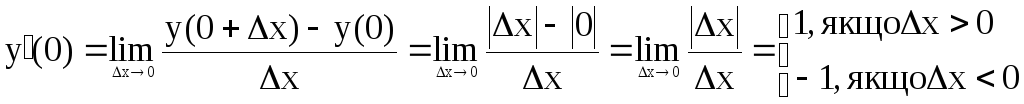Таким чином, функція в точцімає кінцеві, але не рівні одна одній односторонні похідні. Тому вона не має похідної в цій точці і не є в ній диференційовною.

Розглянемо теорему про середнє. [3]

Теорема Лагранжа. Якщо функція безперервна на відрізку, диференційована на проміжку, то знайдеться така точка, що:

.

Контрприклад 5 (Приклад 9).

Диференційовна функція, для якої теорема про середнє не має місця.

Функція дійсної змінної всюди неперервна та диференційовна.Однак не існує такого інтервалу , , для якого при деякому справедлива рівність:

.

Якщо припустити, що ця рівність можлива, то, прирівнюючи квадрати модулів (абсолютних значень) обох її частин, ми отримаємо рівність:

,

яка після елементарних перетворень набуде вигляду:

.

Але, так як не існує додатнього h, такого, що , то ми отримали протиріччя.