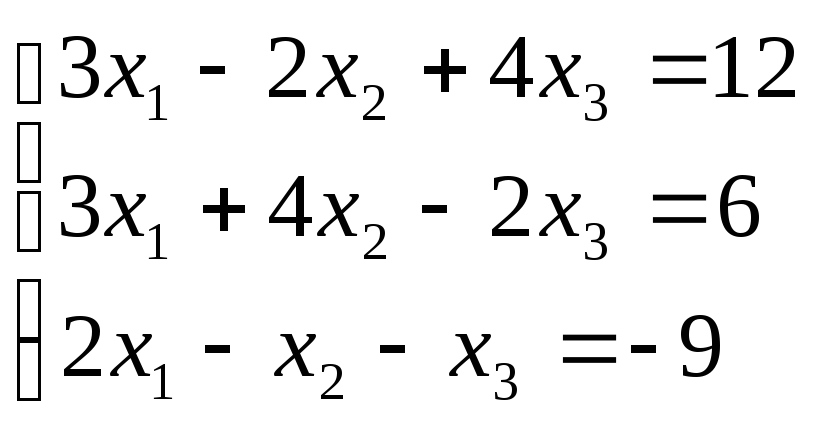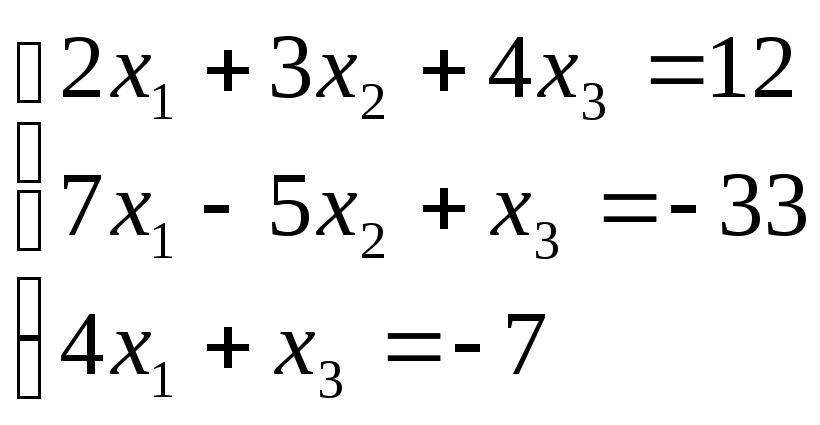Міжнародний науково-технічний університет ім. Академіка ю.Бугая (м. Київ)

Полтавський інститут бізнесу

Кафедра інформаційних управляючих систем

Розрахунково-графічна робота

з дисципліни “Вища математика”

для студентів напряму 6.030601 Менеджмент

ПОЛТАВА – 2010

Укладач:

ст. викладач кафедри інформаційних управляючих систем Передерій О.О.

Розрахунково-графічна робота розглянута та затверджена на засіданні кафедри інформаційних управляючих систем

протокол №___ від “___” _______ 2010 р.

Завідувач кафедри __________________

Пояснювальна записка

Розрахунково-графічна робота призначена для обов’язкового виконання студентами 1 курсу факультету економіки та менеджменту з метою кращого засвоєння вмінь та навиків, отриманих у процесі вивчення дисципліни «Вища математика» і включає в себе завдання, які були пропоновані студентам для самостійної роботи.

Головним завданням графічно-розрахункової роботи є набуття практичних навиків розвязування задач.

Завдання розрахунково-графічної роботи

І. Знайти добуток матриць:

А = ; В = . А = ; В = . А = ; В = . А = ; В = . А = ; В = .

А = ; В = . А = ; В = . А = ; В = . А = ; В = . А = ; В = .

II. Обчислити визначники 2*2

IІІ. Обчислити визначники 3*3

ІV. Обчислити визначники 4*4

V. Обчислити обернену матрицю

VІ. Розв’язати систему рівняння методом Крамера і матричним методом

VІІ. Перевірити сумісність системи рівнянь та в випадку сумісності розв’язати її

• за формулами Крамера

• методом Гауса

VIII. Задачі

1. Знайти , , , ; ; .

2. Знайти , , ; ; .

3. Знайти , , , ; ; .

4. Знайти , , , якщо ; ; .

5. Знайти , , , ; ; .

6. Знайти , , , ; ; .

7. Знайти , , , ; ; .

8. Знайти , , , ; ; .

9. Знайти , , , ; ; .

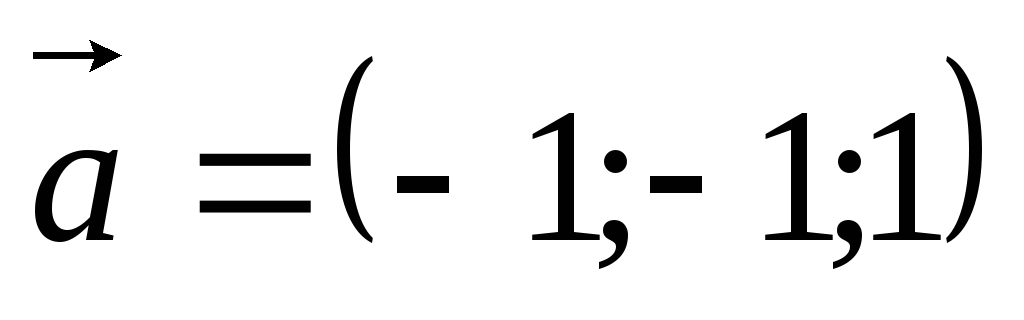10. Знайти , , , ; ; .

IX. Задачі

1. Записати рівняння прямої, що проходить через точки ; .

2. Записати рівняння прямої, що проходить через точки ; .

3. Записати рівняння прямої, що проходить через точки ; .

4. Записати рівняння прямої, що проходить через точки ; .

5. Записати рівняння прямої, що проходить через точки ; .

6. Записати рівняння прямої, що проходить через точки ; .

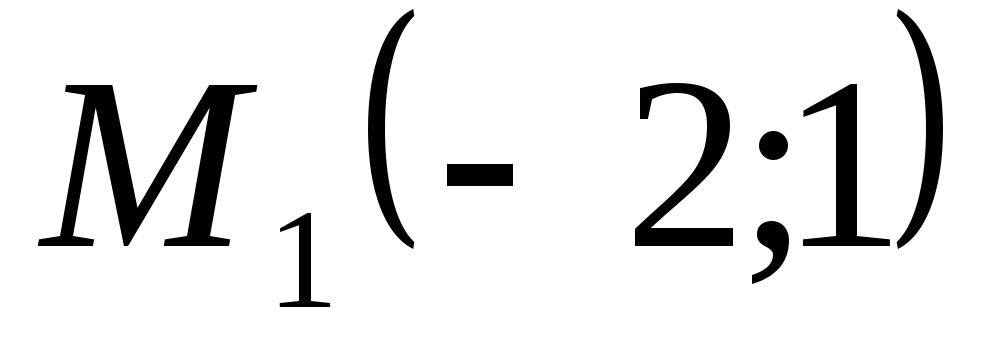7. Розв’язати систему рівняння методом Крамера і матричним методом

8. Записати рівняння прямої, що проходить через точки ; .

9. Записати рівняння прямої, що проходить через точки ; .

10. Записати рівняння прямої, що проходить через точки ; .

11. Записати рівняння прямої, що проходить через точки ; .

X. Провести повне дослідження функції та побудувати її графік

XІ. Знайти похідну функції:

XII. Графічним методом розв’язати задачі лінійного програмування.

1. f_max = 3x₁ + 4x₂ 2. f_min = 2x₁ + x₂

3x₁ + 2x₂ ≤ 6 2x₁ + 5x₂ ≤ 10

2x₁ + 3x₂ ≤ 12 2x₁ – 2x₂ ≥ 2

3x₁ + x₂ ≤ 10 -5x₁ + x₂ ≤ 5

x₁, x₂ ≥ 0 x₁, x₂ ≥ 0

3. f_max = 3x₁ + x₂ 4. f_min = x₁ + 2x₂

x₁ – 2x₂ ≥ - 2 x₁ – 3x₂ ≤ 0

4x₁ + 3x₂ ≥ 12 2x₁ – 3x₂ ≤ 6

2x₁ + 3x₂ ≤ 12 2x₁ + 3x₂ ≤ 12

x₁, x₂ ≥ 0 x₁, x₂ ≥ 0

5. f_min = 3x₁ + 5x₂ 6. f_min =x₁ – x₂

2x₁ – x₂ ≥ -2 3x₁ + 3x₂ ≤ 1

x₁ – x₂ ≤ 1 x₁ – 2x₂ ≤ 2

3x₁ + 2x₂ ≥ 6 5x₁ + x₂ ≤ 5

x₁ + x₂ ≤ 4 3x₁ + 2x₂ ≤ 3

x₁, x₂ ≥ 0 x₁, x₂ ≥ 0

7. f_max = 4x₁ + 3x₂ 8. f_max = 4x₁ + x₂

x₁ – 2x₂ ≤ 4 5x₁ + 2x₂ ≥ 10

4x₁ + x₂ ≥ 4 2x₁ – x₂ ≤ 2

3x₁ + 7x₂ ≤ 21 4x₁ + 5x₂ ≤ 20

x₁, x₂ ≥ 0 x₁, x₂ ≥ 0

9. f_min = 7x₁ + 2x₂ 10. f_max = 3x₁ + 5x₂

-3x₁ + 2x₂ ≤ 6 -5x₁ + 3x₂ ≤ 15

-2x₁ + 5x₂ ≥ 5 2x₁ + x₂ ≥ 2

2x₁ + x₂ ≥ 4 3x₁ + x₂ ≤ 9

0 ≤ x₁ ≤ 2, x₂ ≥ 0 x₁, x₂ ≥ 0

XIII. Симплекс-методом розв’язати наступні задачі лінійного програмування.

11. f_min = 3x₁ + 2x₂ + x₃ 12. f_max = 2x₁ – 4x₂ + 3x₃

5x₁ + 3x₂ – 4x₃ ≤ 15 x₁ – x₂ – x₃ ≤ 7

3x₁ + 5x₂ + x₃ ≤ 21 3x₁ + 2x₂ + 6x₃ ≤ 21

x₁ – 3x₂ ≥ 12 -x₁ + 3x₂ + 4x₃ ≥ 16

2x₁ + 5x₂ + 3x₃ ≤ 25 x_i ≥ 0, i = 1, 3

x_i ≥ 0, i = 1, 3

13. f_min = -2x₁ – 3x₂ + x₃ 14. f_min = x₁ + 2x₂ – 3x₃

2x₁ + x₂ – x₃ ≤ -2 -2x₁ + x₂ + 3x₃ ≤ 4

x₁ + 2x₂ ≤ 5 2x₁ + 3x₂ ≤ 6

-3x₁ – 2x₂ ≥ -4 x₁ + x₃ ≤ 2

x_i ≥ 0, i = 1, 3 x_i ≥ 0, i = 1, 3

15. f_max = 2x₁ + 3x₂ + 5x₃ 16. f_min = 3x₁ + 3x₂ + x₃

x₁ – x₂ – x₃ ≥ -5 2x₁ + 2x₂ + x₃ = 8

-x₁ + x₂ – x₃ ≤ 4 x₁ + 2x₂ + 3x₃ ≤ 12

x₁ + x₂ + 2x₃ = 10 4x₁ + 8x₂ + 3x₃ ≥ 24

x_i ≥ 0, i = 1, 3 x_i ≥ 0, i = 1, 3

17. f_max = 2x₁ – 4x₂ + 5x₃ 18. f_max = 3x₁ + 2x₂ + 2x₃

-x₁ + 4x₂ – 2x₃ ≤ 6 x₁ + 2x₂ – x₃ ≤ 8

x₁ + x₂ + 2x₃ ≥ 6 2x₁ – 3x₂ + x₃ ≤ 12

2x₁ – x₂ + 2x₃ ≤ 4 x₁ + 2x₃ ≤ 10

x_i ≥ 0, i = 1, 3 x_i ≥ 0, i = 1, 3

19. f_min = 3x₁ + 6x₂ – 4x₃ 20. f_min = 3x₁ – x₂ – x₃

3x₁ + 5x₂ – 3x₃ ≤ 12 3x₁ + 5x₂ + 2x₃ ≤ 25

x₁ – 3x₂ + 4x₃ ≤ 21 6x₁ + 2x₂ – 3x₃ ≤ 28

-x₁ + 2x₂ – 3x₃ ≤ 16 2x₁ + 3x₂ + 4x₃ ≤ 36

x_i ≥ 0, i = 1, 3 x_i ≥ 0, i = 1, 3