Контрольные вопросы

1. Опишите алгоритм построения угла в перспективе.

2. Приведите порядок нахождения натурального размера отрезка пи условии, что он горизонтален и расположен под углом к картине.

3. Опишите алгоритм построения в перспективе квадрата со стороной, расположенной под. углом к картине.

4. Укажите, каким образом производится построение в перспективе вертикально расположенного квадрата.

5. Какие существуют особенности построения фигур при использовании дробной дистанционной точки?

6. Приведите последовательность построения перспективы окружности.

Практическая работа №3 построение объемных тел в перспективе

Цель работы: научиться строить в перспективе куб, пирамиду, конус и цилиндр.

Структура работы

В рамках данной практической работы рекомендуется:

1. построить перспективу вертикально стоящего куба, четыре стороны которого расположены параллельно картине;

2. построить перспективу вертикально стоящего куба, расположенного под углом к картине;

3. построить перспективу правильной четырехугольной пирамиды, стоящей на горизонтальной плоскости под произвольным углом к картине;

4. построить перспективу конуса, стоящего на горизонтальной плоскости;

5. построить перспективу цилиндра, стоящего на горизонтальной плоскости;

6. построить перспективу горизонтально лежащего цилиндра, расположенного под углом к картине;

7. построить перспективу тора.

Краткие теоретические сведения Перспектива куба

Построим перспективу вертикально стоящего куба, четыре стороны которого расположены параллельно картине.

Точка схода перпендикулярных картине сторон куба – главная точка картины.

1. Построим перспективу квадрата ABCE .

2. На вертикалях из А и В откладываем величины, равные длине АВ, получаем точки А^I и В^I.

3. На вертикалях из Е и С откладываем величины, равные длине ЕС, получаем точки Е^I и С^I.

4. Соединяем получившиеся точки.

Рис. 3.1. Перспектива вертикально стоящего куба, четыре стороны которого расположены параллельно картине.

Построим перспективу вертикально стоящего куба, расположенного под углом к картине.

1. Строим перспективу квадрата ABCE (пунктиром обозначена линия, отсекающая на отрезках АF₁ и АF₂ длины сторон квадрата – точки В и Е).

2. Из точки А проводим вверх перпендикуляр и откладываем на нем в масштабе высоту куба (штрихпунктирная линия) – получаем точку G.

3. Проводим из точки G лучи в точки схода F₁ и F_2.

4. Из точек B и E проводим перпендикуляры до пересечения с линиями GF₁ и GF₂ – получаем точки J и L.

5. Проводим из точек J и L лучи в точки схода F₁ и F₂ – получаем точку К_.

Перспектива пирамиды

Построим перспективу правильной четырехугольной пирамиды SABСE, стоящей на горизонтальной плоскости под произвольным углом к картине.

1. Строим перспективу квадрата ABCE .

2. Проводим диагонали квадрата. Получаем точку К.

3. Из точки К проводим вверх перпендикуляр и откладываем на нем в масштабе высоту пирамиды - получаем точку S.

4. Проводим из точки С лучи в точки A,B,C и E_.

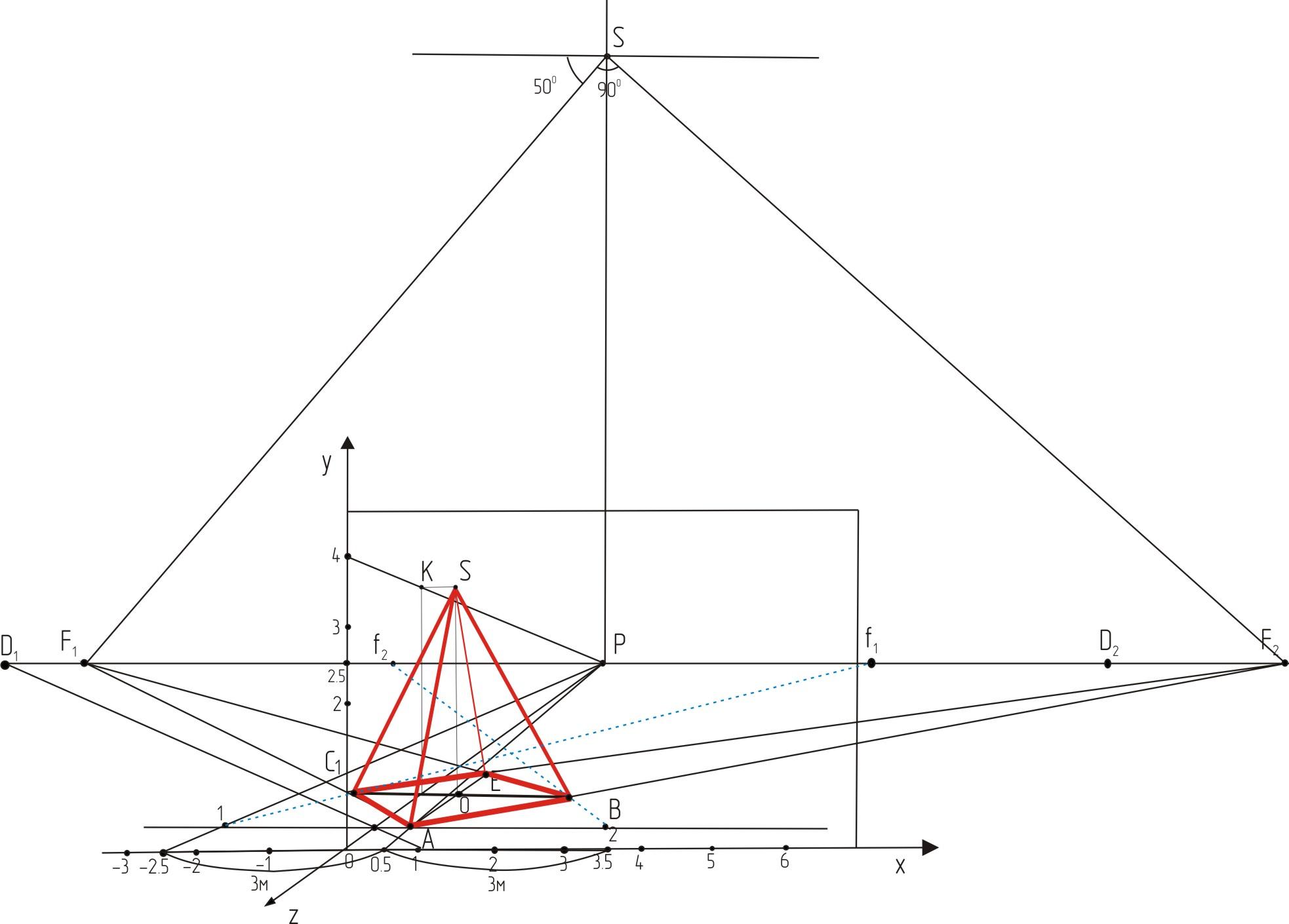
Рис. 3.3. Перспектива правильной четырехугольной пирамиды SABСE, стоящей на горизонтальной плоскости под произвольным углом к картине.