Перспектива квадрата на горизонтальной плоскости

Построим перспективу горизонтального квадрата АВСЕ, 2 стороны которого расположены параллельно картине. Координаты точки А (0,5;0;0,75), АВ=4 м.

1. Проводим основание квадрата АВ:

   1. проводим луч 0,5хР;

   2. проводим луч 4,5хР (4,5=0,5+4);

   3. проводим луч 0,75хD₁ и в пересечении луча с осью 0Z получаем точку 0,75z;

   4. проводим горизонталь из 0,75z и в пересечении с линией 0,5хР получаем точку А, а в пересечении с линией 4,5хР получаем точку В.

2. Проводим лучи в главную точку картины из точек А и В.

3. Диагональ квадрата делит угол на углы 45⁰, значит их точка схода – дистанционная точка D. Проводим луч А.

4. В пересечении луча АD и ВР находим точку С.

5. Проводим из точки С горизонтальную линию до пересечения с лучом АР – находим точку Е.

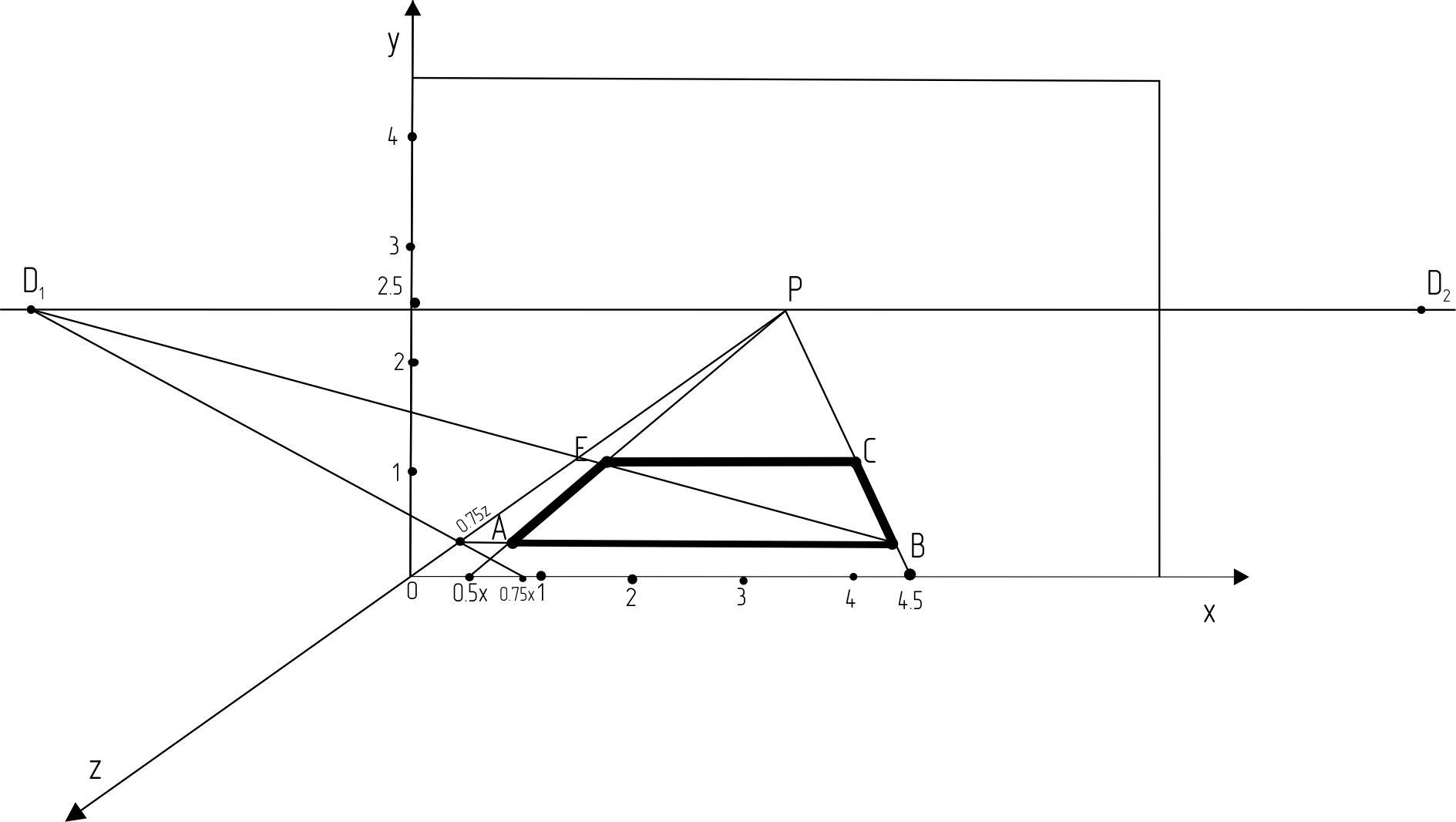
Рис. 2.3. Построение перспективы квадрата.

Построим перспективу горизонтального квадрата АВСЕ, расположенного под углом к картине.

1. Из совмещенной точки зрения S проводим луч под углом 30° к нейтральной плоскости N до пересечения с линией горизонта в точке F₁.

2. Построим при совмещенной точке зрения S прямой угол F₁ S F₂ и найдем точку схода для сторон квадрата AЕ и ВС.

3. Найдем измерительные точки f₁ и f₂: проведем дуги , равные SF₁ и SF₂ ,

4. От точки А на прямой, параллельной картине, отложим вправо и влево отрезки, равные в масштабе длине стороны квадрата, Получим точки 1 и 2.

5. Из измерительных точек f₁ и f₂ прове­дем лучи в концы отрезков – точки 1 и 2. В пересечении прямой f₁2 с АFf₁ получим точку В, а в пересечении прямой f₂1 с AF₂ - точку Е.

6. Проведя противоположные стороны квадра­та в соответствующие точки схода F_t и F₂, получим в их пересечении точку С и перспективу квадрата ABCD.

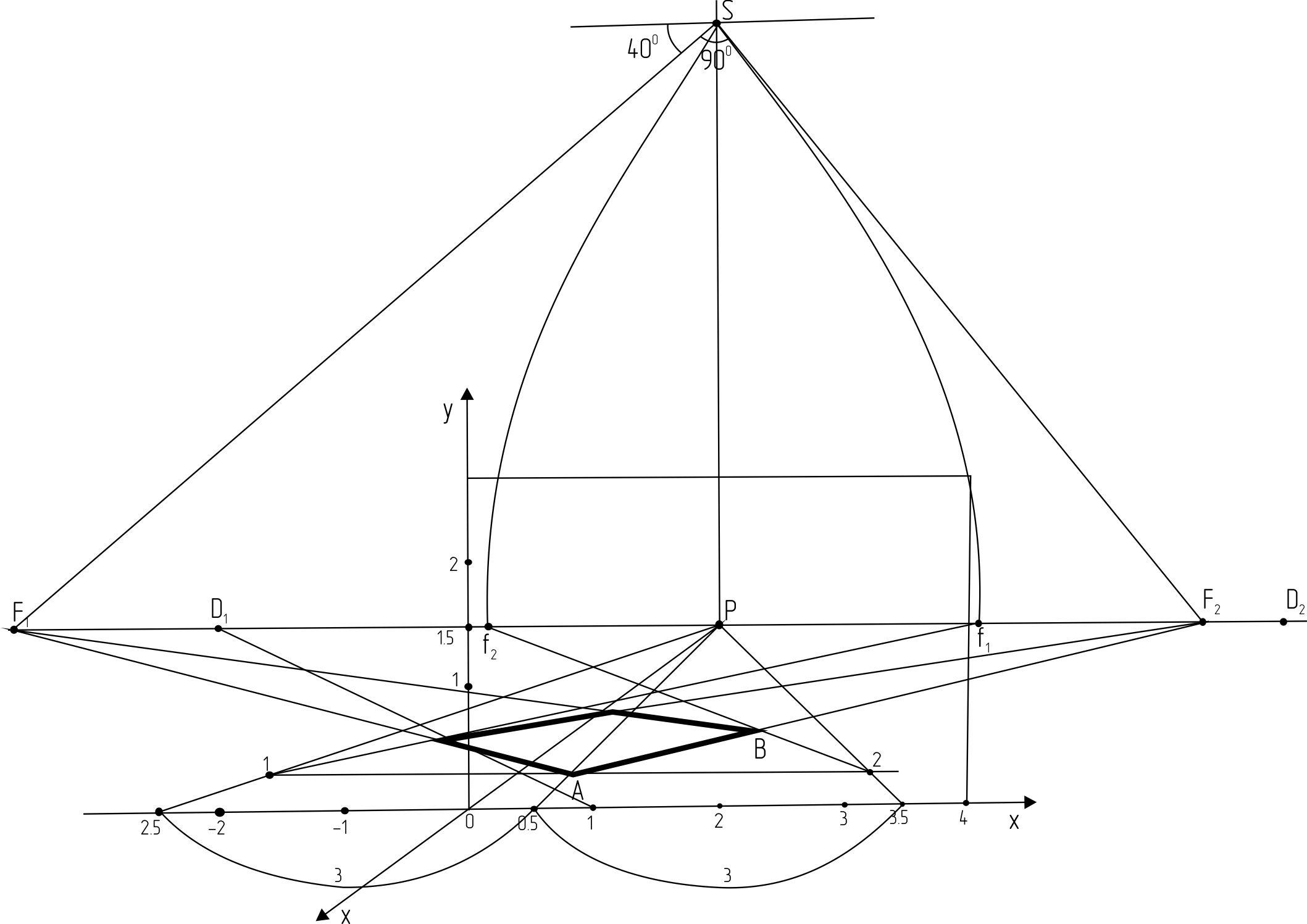
Рис. 2.4. Построение перспективы квадрата, расположенного под углом к картине.

Перспектива квадрата в вертикальной плоскости

Если плоскость перпендикулярна картине, строим так же, как на горизонтальной плоскости, но принимаем осевую линию картины (Р S) за линию горизонта, S за дистанционную точку D, D принимаем за S. Вертикальные стороны AЕ и ВС квадрата, параллельные картине, изображаются вертикальными, т. е. перпендикулярными к линии горизонта, а горизонтальные АВ и DC - сходящимися в главной точке картины Р. Длина изображения АВ отсечется диагональю ЕB с точкой схода в совмещенной точке зрения S = D. Точка S, таким образом, является точкой схода для диагоналей квадрата и дистанционной точкой D.

1. По координатам строим отрезок АЕ.

2. Из точек А и Е проводим лучи в главную точку картины Р.

3. Из точки А проводим луч в совмещенную точку зрения S. В пересечении с отрезком ЕР получаем точку С.

4. Проводим вертикальную линию из точки С до пересечения с линией АР – получаем четвертую точку квадрата В.

Рис. 2.5. Построение перспективы квадрата, расположенного в вертикальной плоскости.

Построение перспективы окружности

Построение перспективы окружности будем выполнять в следующей последовательности:

1. Начертим линию горизонта h₁h₂ определим положение точек Р и D.

2. Построим перспективу квадрата ABС:

• Точки А и В соединим с точкой Р.

• Проведем диагональ квадрата BQ в точку D. Вершина Q определится на пересечении прямых АР с прямой BD.

3. Проведем в перспективе квадрата ABСQ диагональ AС. Из точек пересечения окружности в натуральном виде с диагоналями квадрата АВС¹Q¹ проведем вертикали до пересечения с АВ. Из получившихся точек проведем лучи в Р – в пересечении данных лучей с диагоналями BQ и AC определим перспективу еще четырех точек.

4. Полученные точки обведем по лекалу.

При построении перспективы окружности могут получаться значительные искажения ее при условии, если разместить окружность много левее или правее точки Р. Поэтому прежде чем строить перспективу окружности, необходимо выбрать точку Р так, чтобы она располагалась в пределах не более диаметра окружности, иначе ее перспектива будет искаженной.