Архив ZIP - WinRAR / 61-69

Для одержання аналітичного виразу, що визначає необхідну структуру автомата, записуються вихідні форми перемикальної функції у вигляді досконалої диз'юнктивної (ДДНФ) або кон’юнктивної (ДКНФ) нормальної форми.

Диз'юнктивна нормальна форма являє собою диз'юнкцію (суму) мінтермів, а ДКНФ – кон’юнкцію (добуток) макстермів.

Мінтермом або конституантою одиниці називається логічна функція, що приймає значення 1 тільки на одному наборі змінних. Утворюється як кон’юнкція всіх вхідних змінних із запереченням тих, які в даному наборі дорівнюють нулю. Число мінтермів дорівнює числу наборів.

Макстермом або конституантою нуля називається логічна функція, що приймає значення 0 тільки на одному наборі змінних. Утворюється як диз'юнкція вхідних змінних, де змінні даного набору, рівні 1, узяті із запереченням. Число макстермів дорівнює числу наборів.

При записі ДДНФ складають суму добутків аргументів (х1 х2, х3 ) для тих наборів, на яких функція в приймає значення 1. Якщо аргумент у наборі дорівнює 1, то він записується без інверсії, якщо аргумент дорівнює 0 – то з інверсією. Так для умов, представлених у табл. 15.2, одержимо ДДНФ:

Запис у ДДНФ застосовують у випадку, коли функція має більше одиниць, аніж нулів. Коли ж більше нулів, доцільно застосувати ДКНФ, склавши добуток сум аргументів для тих наборів, на яких функція приймає значення 0. Якщо аргумент у наборі дорівнює 1, то він записується з інверсією, якщо аргумент дорівнює 0 - те без інверсії. Для умов, представлених у табл. 15.2, дістанемо ДКНФ:

На підставі отриманих рівнянь можна побудувати схеми управління на контактних або безконтактних елементах. Однак, враховуючи складність рівнянь, схеми будуть містити велику кількість елементів. Тому необхідно застосувати методи синтезу автоматів з мінімальною кількістю елементів. До них відносяться методи Квайна й Карно.

Метод Квайна складається з наступних етапів.

■По таблиці істинності записується ДДНФ.

■В отриманої ДДНФ відшукуються суміжні мінтерми (відрізняються знаком тільки одного аргументу). Склеюючись по цьому аргументу, суміжні мінтерми утворюють імпликанти – кон’юнкции із числом співмножників, меншим на одного. Імпликанти у свою чергу можуть склеюватися між собою. Імпликанти що несклюються называются простими.

■Отримана скорочена ДДНФ приводиться до тупикової форми шляхом:

-усунення надлишкових імплікант (надлишковою називається імпліканта, «покриваюча» мінтерми, уже покриті іншими імплікантами);

-застосування закону поглинання для простих імпликант, та мінтермів що

залишилися;

-проведення випробування окремих членів. Для цього відкидається один з доданків, а у виразах, що залишилися, підставляються значення аргументів, що перетворюють випробовуваний член в 1. Якщо частина, що залишилася, при цьому тотожно дорівнює 1, то випробовуваний член зайвий, і навпаки. Метод Квайна застосується до числа аргументів не більше 5, 6.

Наприклад, застосовуючи закон тавтології, запишемо вирази (15.1) у вигляді:

Застосовуючи закон склеювання першого мінтерма із четвертим, другого з п'ятим, третього із шостим, і застосовуючи розподільний закон, одержимо:

Складаємо карту Карно у вигляді таблиці, стовпці й рядка якої відповідають усім можливим наборам значень аргументів х1, х2 х3, х4. Для групи х1; х2 відводимо стовпці, для групи х3 х4 - рядки. Набори розташовуємо в такому порядку, щоби у сусідніх клітках комбінації змінних х1, х2 х3, х4 відрізнялися значенням тільки однієї змінної. Кожному набору значень змінних відповідає одна комірка таблиці Карно (рис. 15.4). Клітинки заповнюються відповідно до таблиці істинності. Клітинки, що містять одиниці, потрібно обвести контурами. У контур можна включати 2k клітинок ( k=1,2,3...).

Рис. 15.4. Карта Карно.

Мінімальна диз'юнктивна форма записується як сума добутків. Число, доданків дорівнює числу контурів, а число множників у кожному доданку дорівнює числу змінних, які не змінюють свого значення в даному контурі. Причому значенням змінної 1 у добутку відповідає сама змінна, а значенню 0 - її заперечення (інверсія). У відповідності зі сказаним, отримаємо для карти Карно (рис. 15.4) Булів вираз

По отриманому рівнянню синтезуємо релейну схему управління (Рис. 15.5)

Рис. 15.5 Релейна схема управління

Для реалізації релейної схеми управління на програмувальному реле «EASY» в cередовищі easysoft на мові LD створюється програма у вигляді, представленому на рис. 15.6.

Тут символи I без інверсії відповідають замикаючим контактам, а з інверсією - розмикальним. Символ Q позначає вихідний сигнал керуючого пристрою.

Рис. 15.6. Структурна діаграма релейної схеми управління.

15.3. Синтез послідовностних автоматов

Послідовністні автомати здійснюють перетворення двійкових вхідних змінних не тільки з урахуванням поточної комбінації на вході в даному такті автоматного часу, але й з урахуванням того, що було в попередніх тактах.

Створення послідовністного автомата, здатного запам'ятовувати попередні даному такту комбінації сигналів на вході, забезпечується наявністю в комбінаційному автоматі не тільки зовнішніх (робочих) входів х і виходів y, але й допоміжних (внутрішніх) змінних 2, які повинні мати можливість давати різні комбінації для кожного такту, що підлягає запам'ятовуванню, і реалізованих у вигляді зворотних зв'язків. Ці внутрішні змінні, подавані на вхід комбінаційної схеми, ніби корегують результат від впливу зовнішніх входів, враховуючи попередні ситуації.

Таким чином, завдання зовнішніх входів - задати поточну комбінацію, а внутрішніх - зберегти й задати на вході комбінацію, що однозначно відповідає комбінації, сформованій на на виході в попередньому такті. У цьому випадку вихідна комбінація формується з урахуванням попереднього такту. У наступному такті внутрішні змінні внесуть чергову корективу (якщо їх комбінація буде відмінна від попередньої) і, отже, нові значення виходів уже несуть у собі сліди двох попередніх тактів і т.д. Кількість таких станів М внутрішніх змінних z, називається вагою послідовністного автомата.

Число внутрішніх змінних mz, що забезпечують можливість кодування всіх М станів, називається об'ємом пам'яті автомата й рівно m2=log2М.

Зовнішніми вхідними змінними автомата визначається кількість його можливих вхідних комбінацій, а внутрішніми - через скільки комбінацій зовнішніх починає повторюватися корекція внутрішніми. Якщо число вхідних змінних tх = 3, а внутрішніх mz = 2, то автомат буде мати вісім станів з повторюваною корекцією через чотири такти.

Наслідком цього є характерна риса послідовністних автоматів: у них внаслідок корекції z можливі різні комбінації виходів при однакових комбінаціях на зовнішніх входах. Технічних варіантів реалізації навіть простих послідовністних автоматів може бути дуже багато. Схема, наведена на рис. 15.8, представляє собою найбільш загальний випадок.

Входи Xt логікою комбінаційної схеми формують виходи Yt у даному такті. У формуванні Yt при цьому беруть участь внутрішні змінні Z t-1, комбінація яких сформувалася в попередньому такті t-1. Змінні Zt-1 сформувалися вузлом управління в колі зворотного зв'язку ЗЗ, який може включати: комбінаційну логіку, часові затримки й вхід синхроонізації. Як видно зі схеми, саме вузол ЗЗ забезпечує «запам'ятовування» шляхом прийому на вхід вихідної комбінації автомата в даному такті й передачу її з часовою затримкою на входи автомата в наступному такті.

Розрив кола ЗЗ перетворює послідовністні автомати в комбінаційні. Важливу роль відіграє характер затримки: якщо блок ЗЗ має вхід синхронізації, «що відмикає» і

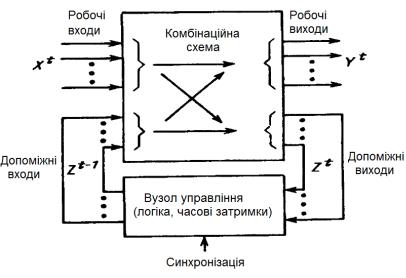
«замикаючий» коло зворотного зв'язку в кожному такті, — це синхронний автомат. У нього рівність Z t-1 = Z t настає тільки після «відмикання» синхроімпульсом кола зворотного зв'язку.

Завдяки зворотному зв'язку, послідовністних автомати мають специфічну властивість, що відрізняють їх від комбінаційних і характерним для замкнених систем керування - вони можуть бути стійкими й нестійкими. Стійким будемо називати стан, коли комбінація виходів змінюється лише внаслідок зміни входу. Нестійкі автомати можуть після встановлення комбінації входів кілька разів міняти комбінацію на виході, проходячи ряд нестійких станів. Такий процес може завершитися переходом у стійкий стан (загасання коливань) або тривати необмежений час (автоколивання).

Рис. 15.8. Функціональна схема послідовностного автомата.

Комбінаційні автомати (розімкнуті) завжди стійкі, як і розімкнуті аналогові ланки. Формальною ознакою стійкого стану є рівність Z t – 1 = Zt а нестійкого - нерівність Z t – 1 ≠ Zt Період автоколивань дорівнює подвійному часу затримки сигналу в ЗЗ.

Для послідовністних автоматів, застосовуються алгебраїчні й табличні форми завдання оператора перетворення. На відміну від комбінаційних автоматів, де цей оператор задається у вигляді зв'язку робочих входів Xt і виходів Yt, для завдання оператора послідовністного автомата потрібно визначити зв'язок не тільки між робочими (зовнішніми) входами й виходами, але й між допоміжними (внутрішніми).

При алгебраїчній формі завдання записуються рівняння виходів, що зв'язують у загальному випадку робочі виходи Yt з робочими Xt і допоміжними Z t – 1 входами й рівняння переходів, що зв'язують виходи внутрішніх змінних Z t – 1 з робочими Xt і допоміжними Zt входами.

При табличній формі завдання складаються таблиці виходів і переходів, при об'єднанні яких виходить таблиця станів.

Уреальних послідовністних автоматах комбінаційні й послідовністні частини не розділяються, а з метою спрощення й скорочення числа елементів поєднуються в одне ціле. Це підвищує використання елементів.

Для побудови складних послідовністних автоматів, широко застосовуються елементарні послідовністні автомати-тригери.

Приклад синтезу послідовністного автомата. Насос Н повинен автоматично включатися при досягненні робочою рідиною нижнього рівня, контрольованого поплавковим датчиком dн, і вимикатися при досягненні верхнього рівня, контрольованого датчиком dв.

Уциклі роботи живильника виділяємо чотири такти:

1- рівень нижче dн (живильник працює, резервуар наповнюється);

2- рівень вище dи, але нижче dв (живильник працює, резервуар наповнюється);

3- рівень досягся з dв (живильник відключився, рідина витрачається, рівень

знижується);

4- рівень нижче dв, але вище dн (живильник відключений, рівень знижується).

Зазначена послідовність відбита в табл. 15.4.

Передбачається, що відбувається безперервне повторення однакових циклів (наповнення - витрата). Для синтезу розглянуто один із циклів.

Вихідна змінна Н приймає різні значення при однакових значеннях вхідних змінних (такти 2 і 4), але при різних їхніх значеннях у попередніх тактах 1 і 3. Це є характерним для послідовністного автомата. Для відпрацьовування необхідної послідовності необхідно «запам'ятати» попередній такт.

Уведемо внутрішній зворотний зв'язок: y=c(xi)(c(xi)+xв),

де c(xi) – кон'юнкція вхідних змінних, що не змінюються у сусідніх тактах; xв – внутрішня змінна.

Тоді для тактів 1,2 матимемо:

= в(н + в′)

Для тактів 3,4:

= н (в + в′′),

де Нв – внутрішня змінна у вигляді зворотного зв'язку по виходу. Застосувавши закон деМоргана до останнього виразу отримаємо:

= н + в в′′.

Контактні схеми представлені на рис 15.9:

Рис. 15.9. Принципові схеми дискретних автоматів.

Схеми працездатні в нормальних умовах, однак при аварійному залипанні нижнього датчика (dн = 0, dв = 1) схема, зображена на рис. 15.7, а не допустить вмикання, а схема рис. 1.7, б допустить вмикання насоса, що спричинить перелив.