37

мо, чтобы в каждой своей бесконечно малой стадии состояние системы, в которой этот процесс происходит, отвечало бы состоянию равновесия.

Состояние равновесия – особое состояние термодинамической системы, в которое она переходит в результате обратимого или необратимого процессов и может оставаться в нем бесконечно долго. Реальные процессы могут приближаться к обратимым, но для этого они должны совершаться медленно.

Процесс называется необратимым (естественным, спонтанным, самопроизвольным), если он сопровождается рассеянием энергии, т. е. равномерным распределением между всеми телами системы в результате процесса теплопередачи.

В качестве примеров необратимых процессов могут быть названы следующие:

• замерзание переохлажденной жидкости;

• расширение газа в вакуумированное пространство;

• диффузия в газовой фазе или в жидкости.

Систему, в которой произошел необратимый процесс, можно возвратить в исходное состояние, но для этого над системой нужно совершить работу.

К необратимым процессам относится большинство реальных процессов, так как они всегда сопровождаются работой против сил трения, в результате чего происходят бесполезные энергозатраты, сопровождающиеся рассеянием энергии.

Для иллюстрации понятий рассмотрим идеальный газ, находящийся в цилиндре под поршнем. Пусть начальное давление газа Р₁ при его объеме V₁ (рис. 4.1).

Д

авление газа уравновешено насыпанным на поршень песком. Совокупность равновесных состояний описывается уравнениемpV = const и графически изображается плавной кривой (1).

Если с поршня снять некоторое количество песка, то давление газа над поршнем резко снизится (от А до В) лишь после чего произойдет увеличение объема газа до равновесной величины (от В до С). Характер этого процесса – ломанная линия 2. Эта линия характеризует зависимость P=f (V) при необратимом процессе.

Рис. 4.1. Зависимость давления газа от его объема при обратимом (1) и необратимом процессах (2, 3).

Из рисунка видно, что при обратимом расширении газа совершаемая им работа (площадь под плавной кривой 1) больше, чем при любом необратимом его расширении.

Таким образом, любой термодинамический процесс характеризуется максимально возможной величиной работы, если он совершается в обратимом режиме. К аналогичному выводу можно прийти, если рассмотреть процесс сжатия газа. Только следует иметь ввиду, что в этом случае величина работы – отрицательная величина (рис. 4.1, ломаная 3).

3. Коэффициент полезного действия тепловой машины. Цикл Карно.

Классический пример применения второго начала термодинамики – определение максимально возможного коэффициента полезного действия (К. П. Д.) тепловой машины. Исторически исследования в этой области послужили исходным пунктом термодинамики. Из положений второго начала следует, что тепловая машина должна содержать не менее двух тел, находящихся при разных температурах: нагревателя при температуре Т₁ и холодильника при температуре Т₂ (Т₁>Т₂). Для получения максимальной работы, перенос энергии от нагревателя к холодильнику должен осуществляться в обратимом режиме. Для осуществления переноса необходимо участие еще одного, так называемого рабочего тела, совершающего обратимый циклический процесс.

Отношение совершенной рабочим телом работы к сообщенной рабочему телу энергии – К.П.Д. тепловой машины ():

, (4.1)

где А – совершенная рабочим телом полезная работа;

q₁ – энергия, полученная рабочим телом от нагревателя в результате теплопередачи;

q₂ – энергия, теплопередачей возвращенная рабочим телом холодильнику.

Схема тепловой машины может быть представлена рис. 4.2.

Рис.4.2. Схема тепловой машины.

П

усть рабочий цикл тепловой машины состоит из двух изотерм (1 - 2 и 3 – 4) и двух адиабат (2 – 3 и 4 – 1). Такой цикл называется циклом Карно (рис. 4.3).

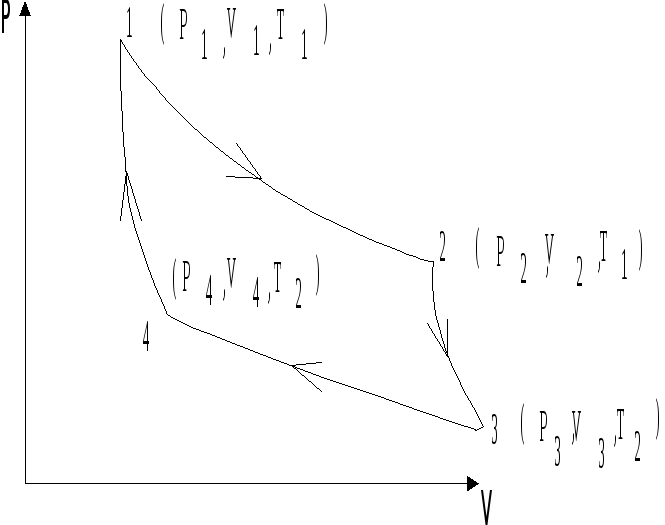
Все указанные на рис. 4.3 процессы являются обратимыми, поэтому исходное и конечное состояния газа совпадают. Рабочим телом является идеальный газ в количестве 1 моля, находящийся в цилиндре под поршнем.

Рис. 4.3. Цикл Карно.

Изотермическое расширение газа (1 –2) происходит в условиях контакта цилиндра с теплоотдатчиком (нагревателем), температура которого Т₁. Газ расширяется до объема V₂ и работа, им совершенная, равна поглощенной от нагревателя энергии:

. (4.2)

При адиабатическом расширении газа (2 – 3) цилиндр с поршнем отсоединяется от нагревателя и работа расширения газа выполняется за счет уменьшения его внутренней энергии:

. (4.3)

Изотермическое сжатие (3 – 4) газа происходит в условиях контакта цилиндра с холодильником (теплоприемником), а энергия, выделяющаяся при сжатии полностью поглощается холодильником:

. (4.4)

Работа, произведенная на последнем участке (4 – 1) цикла производится в условиях отсутствия контакта рабочего тела с холодильником и приводит к повышению запаса внутренней энергии газа и его температура увеличивается до Т₂: .

Суммарная величина работы, выполненная рабочим телом за цикл определяется:

. (4.5)

Из уравнений адиабат:

, (4.6)

, (4.7)

следует:

. (4.8)

Следовательно (4.5) с учетом (4.8) примет вид:

. (4.9)

Тогда К. П. Д. вычисляется:

, (4.10)

окончательно:

. (4.11)

Соотношение (4.11), полученное для цикла Карно, можно рассматривать как аналитическое выражение второго начала термодинамики. Из (4.11) следует, что К. П. Д. тепловой машины зависит только от температур нагревателя и холодильника и он тем больше, чем ниже Т₂.

Можно доказать, что К. П. Д. цикла Карно, состоящего из обратимых процессов, больше К.П.Д. любого другого цикла (),состоящего из нескольких обратимых процессов (теорема Карно):

. (4.12)

Высокое значение К. П. Д. цикла Карно является следствием не его специфической формы, а обратимостью всех его составляющих.

Из соотношения (4.12) следует:

или , (4.13)

откуда:

. (4.14)

Неравенство (4.14) - одна из форм записи второго начала термодинамики.