1.2.Вязкая задача фотопластичности

При моделировании вязкого течения с помощью фотопластичной модели задача решается с позиций ием материалов, вязкость которых более 10⁶ Па • с, то можно пре­небречь силами веса и инерции, поскольку силы внутреннего трения значительно превосходят массовые инерционные силы. Тогда про­цесс вязкого течения может быть полностью описан уравнениями физической связи между напряжениями и скоростями деформации:

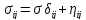(12)

уравнениями постоянства объема:

Дифференциальными уравнениями равновесия:

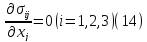
где η – коэффициент вязкости.

Введем в рассмотрение вспомогательный тензор S_ij, соответсвующий девиаторной части тензора напряжений:

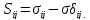
Тогда уравнение (12) можно записать

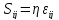(15)

Уравнение (15) показывает, что в случае вязкого течения меж­ду компонентами девиатора напряжений S_ij и компонентами скоростей деформации ε_ij имеет место линейная зависимость, частным слу­чаем которой является соотношение, описывающее плоскопарал­лельное движение вязкоcти жидкости

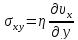
Справедливость уравнения (15) подтверждается молекулярно-ки-нетической теорией вязкого течения. Если принять коэффициент внутреннего трения η постоянным, то, решая совместно уравнения (12) и (13) с уравнениями равновесия (14), можно получить линейное дифференциальное уравнение второго порядка относительно сред­него напряжения σ:

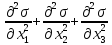= 0 (16)

Из совместного рассмотрения уравнений (12) — (14) можно полу­чить систему уравнений только для скоростей течения. Вязким ма­териалам, течение которых описывается уравнением (16), свойствен­но полное прилипание к поверхности инструмента, поэтому ско­рость течения деформируемого материала равна скорости движения поверхности инструмента. Это свойство определяет граничные усло­вия при решении задачи в скоростях.

Изложенная методика позволяет провести аналитическое иссле­дование многих процессов течения. Однако в случае геометрически сложного очага деформации расчеты оказываются практически не­выполнимыми. Кроме того, коэффициент внутреннего трения боль­шинства реальных материалов — переменная величина, зависящая от среднего напряжения и температуры. Зависимость коэффициента внутреннего трения от среднего напряжения имеет вид

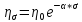(17)

где η₀ — вязкость при среднем напряжении, равном нулю.

Для смол коэффициент α* имеет величину порядка 0,122 МПа ^-1, из чего следует, что допущение о постоянстве коэффициента внутреннего трения в этом случае неприменимо. Если же подставить значение переменного коэффициента внутреннего трения в уравнение (12), то в результате совместного решения си­стем уравнений, описывающих процесс вязкого течения, получим нелинейные дифференциальные уравнения, решение которых даже для простейших процессов встречает значительные математические трудности. Вследствие этого экспериментальное изучение вязкого течения с помощью фотопластичной модели является весьма эф­фективным.

Впервые задача моделирования процесса вязкого течения на фо­топластичных моделях из низкомолекулярных веществ была реше­на С. И. Губкиным, С. И. Добровольским, Б. Б. Бойко [11]. Создан­ный этими авторами метод основан на свойстве некоторых аморфных веществ сохранять оптическую чувствительность в процессе вяз­кого течения. Наиболее подходящим для целей моделирования ока­зался сплав, состоящий из четырех частей канифоли и одной части канифольного масла, на котором и проводились основные экспе­риментальные исследования. При незначительном изменении темпе­ратуры коэффициент внутреннего трения в этом сплаве зависел толь­ко от величины среднего напряжения ст. Введя переменный коэффици­ент внутреннего трения по формуле (17) в уравнение (12) и заменив ε_ij через ,

Получим

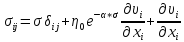(18)

Уравнение (18) используется для установления условий подобия реального и модельного процессов:

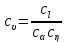(19)

где константы подобия с_l, с_а*, с_η должны выбираться эксперимен­татором, исходя из условий удобства проведения опытов и обработ­ки опытных данных, а также из возможностей имеющегося обо­рудования. Константа подобия с_υ представляет собой отношение скоростей течения в соответственных точках натуры и модели, и по­этому равна отношению скоростей хода машин, создающих нагруже­ние. Из критериального уравнения (19) следует, что варьируя ско­ростью хода машины и используя только один материал для модели, можно получить распределение напряжений для натурного про­цесса практически с любыми значениями а* и η.

В работе [41] предложено использовать в качестве вязких оп­тически чувствительных материалов низкомодульные материалы на основе этилцеллюлозы, глифталевых и эпоксидных смол, которые успешно применялись при моделировании тектонических полей на­пряжений.

Рассмотренные вязкие оптически чувствительные материалы и методика моделирования могут быть использованы для решения тех­нологических задач обработки металлов давлением, связанных с качеством готовой продукции, определением энергосиловых пара­метров и расчетом рабочего инструмента.