1210-методичка

Колебания.

Ι. Механические.

1. Гармонические колебания.

1.1. Дифференцируемое уравнение гармонических колебаний материальной точки массой m:

или

– коэффициент упругости.

1.2. Решение этого дифференциального уравнения – кинематическое уравнение гармонических колебаний:

,

где x – отклонение колеблющейся величины от равновесного значения;

A – амплитуда колебаний;

– циклическая частота;

Т – период колебаний;

– частота колебаний;

– начальная фаза.

– фаза колебаний.

1.3. Скорость и ускорение при гармонических колебаниях:

;

.

1.4. Кинетическая энергия тела, совершающего гармонические колебания:

1.5. Потенциальная энергия:

;

1.6. Полная энергия:

;

или

1.7. Периоды колебаний маятников:

а) пружинного:

,

где m – масса колеблющегося тела (маятника);

б) математического:

,

где l – длина маятника;

– ускорение свободного падения;

в) физического:

,

где I – момент инерции маятника относительно оси колебаний;

l – расстояние между точкой подвеса и центром масс маятника.

2. Сложение колебаний.

2.1. Колебания одинакового направления и одинаковой частоты:

2.1.1. Амплитуда результирующего колебания:

,

где и – амплитуды складываемых колебаний,

и – их начальные фазы.

2.1.2. Начальная фаза результирующего колебания определяется формулой:

2.2. Колебания взаимно перпендикулярные с одинаковыми частотами.

Уравнение траектории результирующего движения:

,

где А и В – амплитуды складываемых колебаний;

– разность фаз складываемых колебаний.

3. Затухающие колебания.

3.1. Дифференциальное уравнение

,

где х – колеблющаяся величина, описывающая физический процесс;

– коэффициент затухания (),

r – коэффициент сопротивления среды,

m – масса тела,

– циклическая частота свободных незатухающих колебаний.

3.2. Решение дифференциального уравнения:

,

где – циклическая частота затухающих колебаний.

– амплитуда затухающих колебаний.

3.3. Параметры затухания:

- коэффициент затухания:

;

- время релаксации (время, за которое амплитуда колебаний уменьшится в раз):

- логарифмический декремент затухания:

- N – число колебаний, совершаемых за время релаксации.

- добротность колебательной системы:

,

где – энергия колебаний;

– потери энергии за период колебаний.

4. Вынужденные колебания.

4.1. Дифференциальное уравнение и его решение для установившихся колебаний:

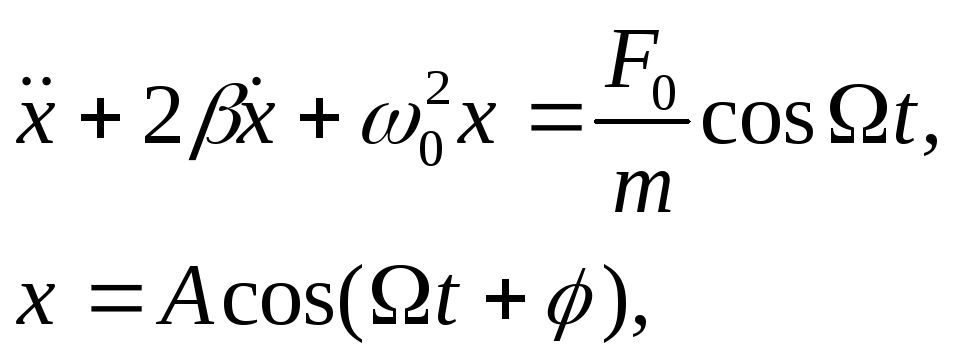
где – вынуждающая сила,

– частота колебаний вынуждающей силы и установившихся вынужденных колебаний.

4.2. Амплитуда вынужденных колебаний:

4.3. Начальная фаза вынужденных колебаний:

4.4. Резонанс – резкое возрастание амплитуды колебаний системы при совпадении частоты собственных колебаний системы с частотой вынуждающей силы.

Резонансная частота:

Амплитуда при резонансе:

Статическое смещение (при )

II. Электромагнитные колебания.

1. Колебательный контур – последовательно соединенные активное сопротивление R, катушка с индуктивностью L, конденсатор ёмкостью C.

C

R L

2. Дифференциальное уравнение свободных гармонических колебаний заряда q в контуре без активного сопротивления (R=0) и его решение:

,

где – собственная циклическая частота колебаний контура.

,

где – амплитудное значение заряда на конденсаторе.

3. Формула Томсона:

.

4. Дифференциальное уравнение затухающих колебаний и его решение аналогичны уравнению и его решению для механических затухающих колебаний.

5. Параметры затухания:

- – коэффициент затухания;

- – добротность,

или , – волновое сопротивление;

6. Дифференциальное уравнение вынужденных колебаний и его решение аналогичны уравнению и его решению для механических колебаний.

7. Полное сопротивление z контура:

,

где – индуктивное сопротивление;

– емкостное сопротивление.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.

Задача №1.

Материальная точка массой m = 10 г совершает гармоническое колебание с периодом 1 с. Начальная фаза колебаний .

Определить амплитуду колебаний, максимальные скорость и ускорение колеблющейся точки, если максимальная кинетическая энергия равна 0,02 Дж.

Дано: m = кг, Т = 1 с, , .

Найти: А,

Решение:

Полная энергия Е колеблющейся точки равна максимальной кинетической или максимальной потенциальной энергии.

Полная энергия зависит от массы колеблющейся точки, амплитуды и циклической частоты колебаний:

Отсюда находим амплитуду колебаний:

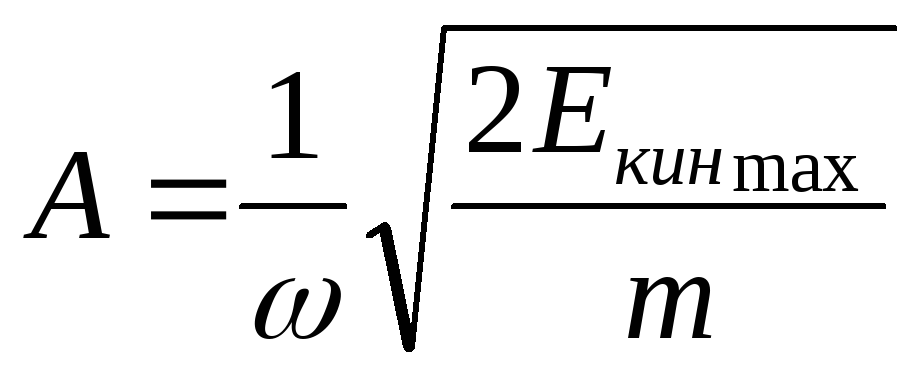
Учитывая , что циклическая частота

Подставим числовые значения и произведем вычисления:

Зная амплитуду, запишем уравнения гармонических колебаний, совершаемых материальной точкой:

где x – смещение точки относительно положения равновесия;

А=0,32 м – амплитуда;

– циклическая частота;

– начальная фаза колебаний.

Скорость точки определяется, как первая производная от смещения по времени:

Максимального значения скорость достигает при получаем

Ускорение точки определяется, как первая производная от скорости по времени:

При ускорение будет максимальным, находим

Максимальную скорость можно найти из выражения для кинетической энергии:

Откуда

Подставляя числовые значения, произведем вычисления:

.

Ответ: А = 0,32 м, =2 м/с, .

Задача №2.

Материальная точка массой m = 10 г совершает гармонические колебания с частотой . Амплитуда колебаний А = 5см. Определить: 1) максимальную силу, действующую на точку; 2) полную энергию колеблющейся точки.

Дано: , , .

Найти:

Решение:

Уравнение гармонических колебаний

.

Скорость и ускорение колеблющейся точки:

Сила, действующая на точку, по второму закону Ньютона:

Максимального значения сила достигает при , следовательно:

т.к. собственная циклическая частота , то .

Полная энергия колеблющейся точки:

Подставив в эту формулу выражение для , получим:

Подставим числовые значения, произведём вычисления:

Ответ: , .

Задача №3.

Складываются два колебания одинакового направления, выраженные уравнениями: , см и , см. Построить векторную диаграмму сложения этих колебаний и написать уравнение результирующего колебания.

Дано: , см; , см.

Найти: .

Решение.

При сложении двух одинаково направленных гармонических колебаний одинакового периода получается гармоническое колебание того же периода с амплитудой

А=.

По условию задачи

А₁ = 2 см; А₂ = 4 см; φ₀₁ = 0⁰; φ₀₂ = 60⁰.

Подставив числовые значения величин, произведем вычисления:

А=(см).

Начальную фазу результирующего колебания определяем по формуле

.

Произведем вычисления:

Результирующее колебание можно записать в виде

, см.

Для построения векторной диаграммы отложим от начала отсчета векторы, длины которых равны амплитудам А₁ и А₂, под углами φ₀₁ = 0⁰ и φ₀₂ = 60⁰ к оси Ох. Сложив векторы по правилу параллелограмма, получим вектор амплитуды результирующего колебания.

у

6

4 А₂ А

2

φ₀₁

φ₀₂ А₁

0 2 4 6 х

Ответ: , см.

Задача №4.

Математический маятник, состоящий из нити длиной l = 243 см и стального шарика радиусом r = 2 см, совершает гармонические колебания с амплитудой A = 10 см. Определите скорость шарика при прохождении им положения равновесия и наибольшее значение равнодействующей всех сил, действующих на шарик. Плотность стали .

Дано: l = 2,43 м, r = 0,02 м, A = 0,1 м, .

Найти:

Решение:

Период колебаний математического маятника

,

где g – ускорение свободного падения

(l+r) – расстояние от точки подвеса до центра тяжести шарика.

Циклическая частота:

(1)

При прохождении маятником положения равновесия его скорость достигает максимального значения, равного:

(2)

Наибольшее значение возвращающая сила имеет в крайнем положении маятника, где смещение становится равным амплитуде, а ускорение достигает максимума:

(3)

Массу колеблющегося шарика мы найдем, зная радиус и плотность материала:

, (4)

где – объем шарика.

Решая уравнение (1) – (4) совместно относительно скорости и силы, после подстановки числовых данных получим:

Ответ: ,

Задача №5.

Тонкий однородный стержень длинной l = 60 см может свободно вращаться вокруг горизонтальной оси, отстоящей на расстоянии а = 15 см от, его середины. Определить период колебаний стержня, если он совершает малые колебания.

Дано: l = 0,6 м, а = 0,15 м.

Найти: Т.

Решение:

Стержень представляет собой физический маятник, период колебания которого определяется по формуле:

T=2π,

где I – момент инерции стержня относительно данной оси;

g – ускорение свободного падения;

а – расстояние от центра масс до точки подвеса;

m – масса стержня.

О С

а

По теореме Штейнера

I = I₀+mа²

где I₀=1/12ml² – момент инерции стержня относительно оси проходящей через центр масс параллельно данной

I=1/12ml²+ mа²

Тогда:

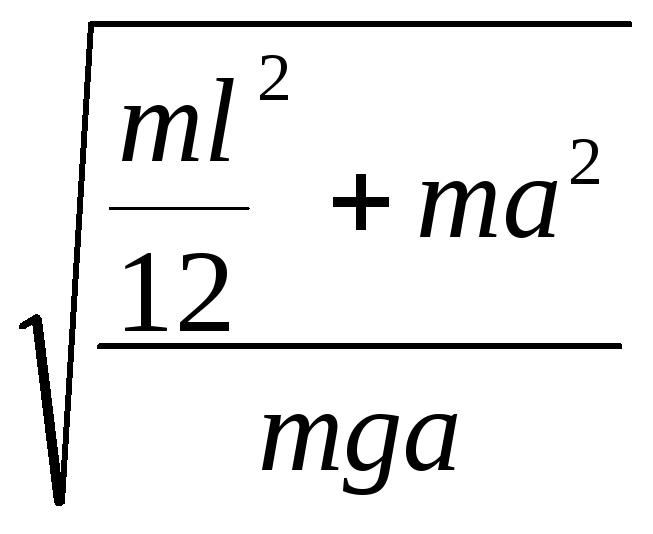T=2π=2π.

Подставим числовые значения и произведем вычисления:

T=2·3,14=1,19 (с)

Ответ: Т = 1,19 с.

Задача №6.

На вертикально и горизонтально отклоняющее пластины осциллографа поданы напряжение и . Определить траекторию луча на экране осциллографа.

Дано:, .

Найти:

Решение:

Для определения траектории луча из уравнений и исключим время:

Преобразуем второе уравнение с учетом (1). Т. к.

.

– уравнение параболы.

Ответ: траектория луча – парабола.

Задача №7.

Начальная амплитуда колебаний механического маятника см, амплитуда после 10 полных колебаний равна см. Определить логарифмический декремент затухания и коэффициент затухания, если период колебаний с. Записать уравнение колебаний.

Дано: см, см, N=10, T=5 c.

Найти: .

Решение:

Амплитуда затухающих колебаний уменьшается со временем по закону:

,

где – начальная амплитуда колебаний (в момент времени t = 0),

– коэффициент затухания.

По условию задачи

Для момента времени (т.е. через N периодов) амплитуда равна:

(1)

Отсюда:

.

Прологарифмируем это выражение:

Отсюда коэффициент затухания

Подставляя числовые значения, получим

(с

Логарифмический декремент затухания:

.

Произведем вычисления

.

Зависимость смещения x маятника от времени t выражается уравнением:

,

где – циклическая частота затухающих колебаний.

Циклическая частота затухающих колебаний связана следующим с циклической частотой свободных незатухающих колебаний и коэффициентом затухания :

,

а период затухающих колебаний – соотношением

.

Из формулы периода определим :

Тогда

(м)

Ответ: (м).

Задача №8.

Логарифмический декремент затухания колебании, имеющих частоту 50 Гц, равен 0,01. Определить : 1) время, за которое амплитуда колебаний тела уменьшиться в 20 раз; 2) число полных колебаний тела, чтобы произошло данное уменьшение амплитуды.

Дано: , , .

Найти: