Методика выполнения работы

1. Изучить предоставленные средства измерения длины.

2. Подготовить средства измерений к работе: осмотреть измерительный инструмент, очистить от загрязнения. Подготовить образец к процессу измерений.

3. Определить погрешность измерения разных измерительных инструментов.

4. Определить размеры стальной пластины разными средствами измерений. Результаты внести в журнал лабораторных работ.

5. Записать результаты измерений в журнал лабораторных работ, используя принятые в метрологии правила округления.

6. По выполненной работе в журнале сделать выводы.

Контрольные вопросы

1. Что такое измерение.

2. Приведите формулировку прямых измерений.

3. Какие методы прямых измерений Вы знаете. Приведите примеры.

4. Что такое основная и дополнительная погрешность средств измерения.

5. Как определить приборную погрешность, зная его класс точности.

6. Как определяется суммарная предельная погрешность измерения.

7. Как производится округление результата и погрешностей измерения.

ЛАБОРАТОРНАЯ РАБОТА №2

СТАТИСТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ

МНОГОКРАТНЫХ ПРЯМЫХ ИЗМЕРЕНИЙ

Цель работы: изучение методики обработки результатов многократных прямых измерений.

Инструмент, приборы и оборудование: микрометр 0-25 мм; исследуемый образец.

Общие сведения

При проведении с одинаковой тщательностью и в одинаковых условиях повторных измерений (повторных наблюдений) одной и той же постоянной, неизменяющейся величины мы получаем результаты наблюдений, некоторые из которых отличаются друг от друга, а некоторые совпадают. Такие расхождения в результатах измерений говорят о наличии в них случайных погрешностей. Поскольку производится измерение определенного параметра конкретного объекта, то существует некоторое истинное значение этого параметра, которое невозможно определить из-за погрешностей отдельных наблюдений.

Теория вероятностей дает математические методы изучения свойств случайных событий в больших совокупностях. Теория погрешностей, использующая математический аппарат теории вероятностей и математической статистики, основывается на рассмотрении появления случайных погрешностей при многократно повторяемых наблюдениях как случайных событий.

Статистическая обработка экспериментальных выборок выполняется в такой последовательности:

• исключить (или уменьшить) систематические составляющие погрешности из результатов наблюдений одним из известных способов: введения поправок, замещения, компенсации, противопоставления;

• проверить соответствие экспериментального закона распределения теоретическому, нормальному (аналитическим или графоаналитическим способом). При сравнительно небольшом числе наблюдений такую проверку можно выполнить аналитическим способом – с помощью «критерия W». Расчет с помощью «критерия W» выполняется для выборок объемом от 3 до 50 результатов наблюдений. При этом необходимо, прежде всего, упорядочить выборку, расположив все наблюдения x_i в неубывающем порядке (в виде вариационного ряда): x₁ £ x₂ £ … £x_n. Исходные данные следует записать в расчетную таблицу 2.2 журнала лабораторных работ. В нижней половине четвертой графы таблицы снизу вверх записываются значения j от 1 до l, причем l = n/2, если n четное, и l = (n – 1)/2 при нечетном n. Из приложения В при соответствующих n и l следует найти значение коэффициента a_n-j+1 для j от 1 до l и записать их снизу вверх в графе 5, а затем подсчитать разности x_n-j-1 - x_j, которые должны быть внесены в графу 6. Результаты построчного перемножения содержимого граф 4 и 5 записываются в графе 7 таблицы 2.2 Журнала. Вычисляются характеристики

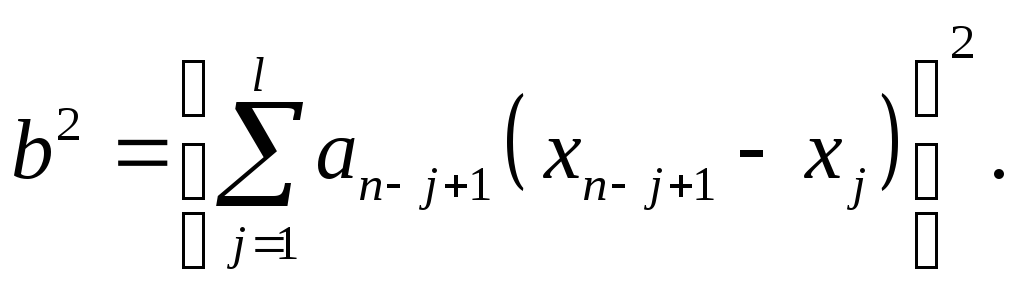
Отсюда критерий

Задавшись определенным уровнем значимости a, отображающим наибольшую вероятность ошибочности гипотезы о принадлежности данной выборки к нормальной генеральной совокупности, по приложению Г находим значение W*. При W* > W можно предполагать, что гипотеза справедлива и опытное распределение не противоречит нормальному закону распределения. При W* < W опытное распределение не соответствует нормальному закону.

Для случая, когда можно предполагать, что данная выборка является частью генеральной совокупности, распределенной по нормальному закону, обработка продолжается;

• вычислить наиболее вероятное значение 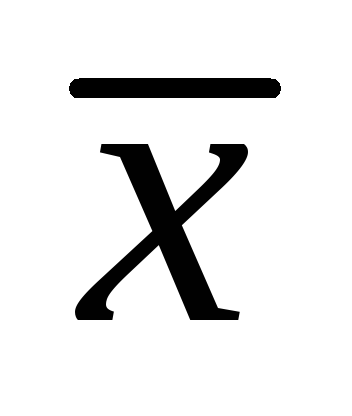искомой величины как среднее арифметическое выборки

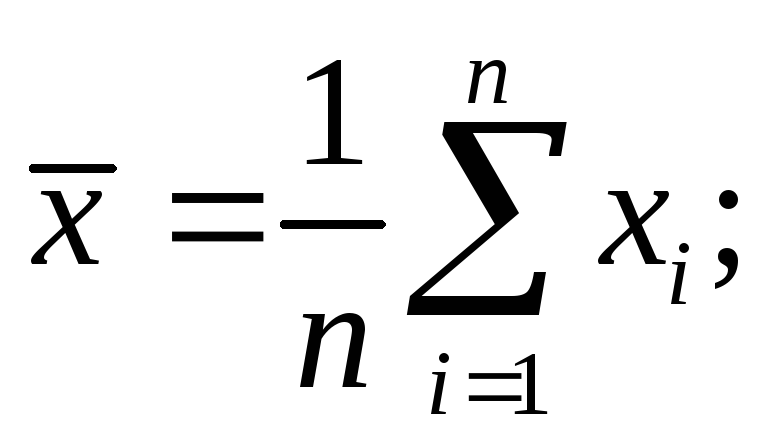
• вычислить среднеквадратичное отклонение s результата наблюдения (с.к.о.) по формуле

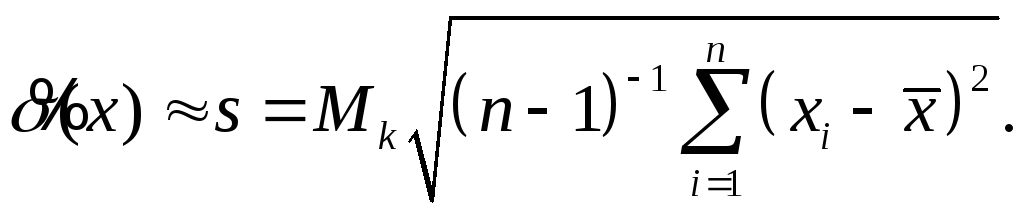
Значения коэффициента M_k приведены в Приложении Д;

• при подозрении анормальности некоторого результата наблюдения x_k, который заметно отличается от остальных в выборке, вычислить показатель анормальности для этого результата

После этого сопоставить значение показателя V_k с табличной величиной β для данного объема выборки и принятой вероятности γ. Если подозрения подтвердятся (критерием анормальности является условие V_k ³ β), этот результат наблюдения должен быть из выборки исключен, а значения x и s вычислены заново (для этой же выборки, но без x_k). Значения величин β приведены в Приложении Е;

• вычислить коэффициент вариации v для данной выборки

• вычислить среднеквадратичное отклонение результата измерения

• вычислить доверительные границы ε случайной составляющей погрешности общего результата измерения

где

t_γ - коэффициент доверия, значения которого приведены в Приложении Ж в зависимости от числа степеней свободы k = n – 1 и γ;

γ - двусторонняя доверительная вероятность.

Обычно для технических расчетов вычисление доверительных границ производится с доверительной вероятностью равной γ = 0,95, в отдельных случаях, когда эксперимент невозможно повторить, принимают γ = 0,99 и только в особо ответственных случаях, когда результаты эксперимента влияют на жизнь и здоровье людей, допускается принимать γ = 0,999;

• определить доверительные границы общей погрешности результата измерения. При тщательной попытке исключить систематическую составляющую погрешности какая-то часть ее все равно остается неисключенной. Доверительную границу Θ этих остатков можно вычислить в результате анализа условий проведения эксперимента. Таких неисключенных остатков может быть несколько (Θ_i – их доверительные границы) Если Θ_i существенно отличаются друг от друга (например, на два порядка или еще больше), то меньшие из них следует отбросить, а оставшиеся просуммировать:

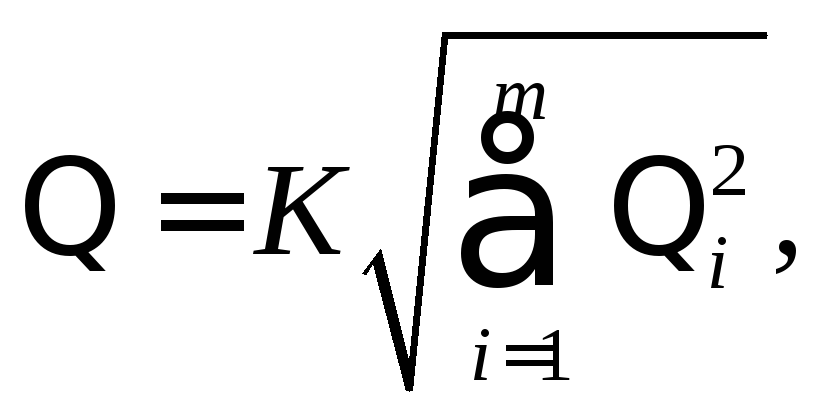
где Θ_i - граница i-й неисключенной систематической погрешности;

m - число этих составляющих;

K - коэффициент, зависящий от принятой доверительной вероятности γ, числа составляющих и соотношения между ними (для доверительной вероятности

γ = 0,95 при m = 4 принимают коэффициент K = 1,1).

• Если доверительные границы неисключенных остатков систематической составляющей погрешности результата измерения близки к нулю (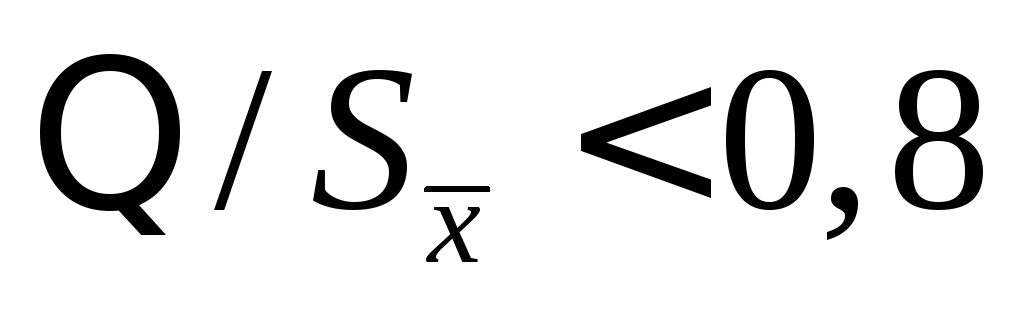), величиной Θ пренебрегают и можно принять

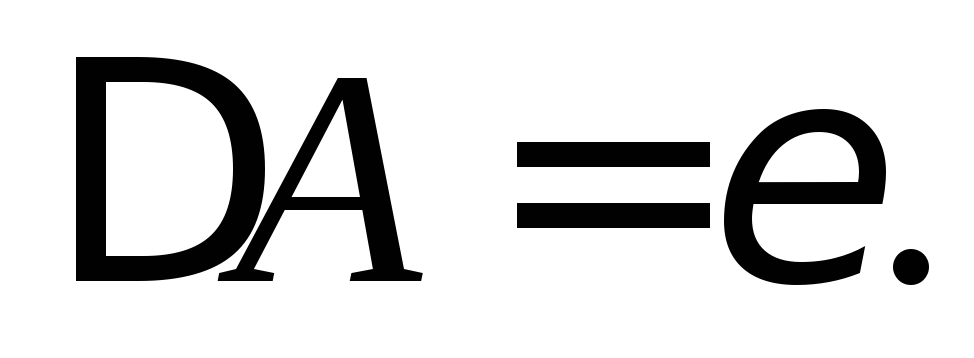
Если пренебрегают величиной ε, и

Если доверительная граница ΔA вычисляется по формуле

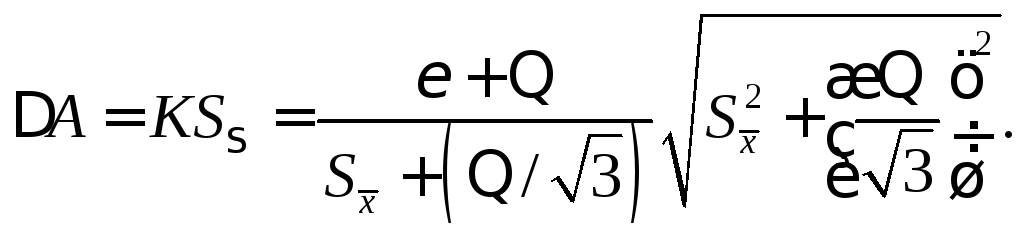
• записать результат прямого измерения в виде

где А – наиболее вероятное значение результата измерения ;

ΔA – доверительная граница погрешности измерения.

Полная форма записи обязательна в том случае, если γ ¹ 0,95. При γ = 0,95 значение вероятности в записи результата измерения часто опускают.