- •1.Предел функции. Теоремы о пределах.
- •2.Непрерывность функции. Точки разрыва функции
- •3. Производная функции в точке. Правила, дифференцирования.
- •4.Производная сложной и обратной функции.
- •5.Геометрический и физический смысл производной.
- •6.Монотонность функции. Экстремумы функции.
- •8.Асимптоты.
- •Частные производные. Примеры решений
- •10.Производная сложной и неявной функции двух переменных
- •11.Использование частных производных в геометрии.
- •12.Экстремумы функции двух переменных.
8.Асимптоты.
Аси́мпто́та[1] (от греч. ασϋμπτωτος — несовпадающий, не касающийся) кривой с бесконечной ветвью — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность[2]. Термин впервые появился у Аполлония Пергского, хотя асимптоты гиперболы исследовал ещёАрхимед[3].
|
Для
гиперболы |
Затухающие
колебания. |
9.
Полное приращение и полный дифференциал ФНП
Полным
приращением функции двух переменных z
= f (x, y) в точке (x, y), вызванным
приращениями аргументов ![]() и
и ![]() ,
называется выражение
,
называется выражение ![]() .
.
Функция z = f (x, y) называется непрерывной в точке (x, y), если бесконечно малым приращениям аргументов соответствует бесконечно малое полное приращение функции.
Если
обозначить ![]() –
расстояние между близкими точками
–
расстояние между близкими точками ![]() и
(х, у), то
и
(х, у), то ![]() –
это определение непрерывности ФНП на
языке приращений.
–
это определение непрерывности ФНП на
языке приращений.
Если функция z = f (x, y) непрерывна в любой точке (х, у)D, то она называется непрерывной ФНП в области D.
Функция
z = f (x, y), полное приращение z
которой в данной точке (x, y) может быть
представлено в виде суммы двух слагаемых:
выражения, линейного относительно ![]() и
и ![]() ,
и величины, бесконечно малой более
высокого порядка малости относительно
,
и величины, бесконечно малой более
высокого порядка малости относительно ![]() ,
называется дифференцируемой ФНП в
данной точке, а линейная часть ее полного
приращения называется полным дифференциалом
ФНП.
,
называется дифференцируемой ФНП в
данной точке, а линейная часть ее полного
приращения называется полным дифференциалом
ФНП.
Если ![]() ,
где
,
где ![]() –бесконечно
малые при
–бесконечно
малые при ![]() ,
то полный дифференциал функции z =
f (x, y) выражается формулой:
,
то полный дифференциал функции z =
f (x, y) выражается формулой:  ,
или:
,
или:
 (1)
(1)
(приращения независимых переменных совпадают с их дифференциалами: х = dx, y = dy).
Из
определения полного дифференциала
следует его связь с полным приращением:
при малых ![]() и
и ![]() полное
приращение функции z
примерно равно ее полному дифференциалу:
полное
приращение функции z
примерно равно ее полному дифференциалу:![]() с
точностью до бесконечно малых более
высокого порядка малости относительно
с
точностью до бесконечно малых более
высокого порядка малости относительно ![]() .
.
Полный
дифференциал функции z = f (x, y)
зависит как от точки M(x0, y0), в которой
он вычисляется, так и от приращений ![]() и
и ![]() .
.
Производные ФНП высших порядков
Пусть
функция z = f (x, y) имеет в точке
(x, y) и её окрестности непрерывные
частные производные первого порядка ![]() и
и ![]() .
Так как
.
Так как ![]() и
и ![]() являются
функциями тех же аргументов x и y, то их
можно дифференцировать по x и по y. При
этом возможны следующие 4 варианта:
являются
функциями тех же аргументов x и y, то их
можно дифференцировать по x и по y. При
этом возможны следующие 4 варианта:
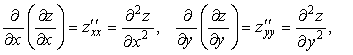

– эти частные производные называются частными производными второго порядка от функции z (x, y).
Частные производные. Примеры решений
На данном уроке мы познакомимся с понятием функции двух переменных, а также подробно рассмотрим наиболее распространенное задание – нахождение частных производныхпервого и второго порядка, полного дифференциала функции. Студенты-заочники, как правило, сталкиваются с частными производными на 1 курсе во 2 семестре. Причем, по моим наблюдениям, задание на нахождение частных производных практически всегда встречается на экзамене.
Для эффективного изучения нижеизложенного материала Вам необходимо уметь более или менее уверенно находить «обычные» производные функции одной переменной. Научиться правильно обращаться с производными можно на уроках Как найти производную? иПроизводная сложной функции. Также нам потребуется таблица производных элементарных функций и правил дифференцирования, удобнее всего, если она будет под рукой в распечатанном виде. Раздобыть справочный материал можно на страницеМатематические формулы и таблицы.
Начнем с самого
понятия функции двух переменных, я
постараюсь ограничиться минимумом
теории, так как сайт имеет практическую
направленность. Функция двух переменных
обычно записывается как ![]() ,
при этом переменные
,
при этом переменные![]() ,
,![]() называются независимыми
переменными или аргументами.
называются независимыми
переменными или аргументами.
Частной производной
по ![]() от
функции
от
функции![]() называется
предел отношения частного приращения
этой функции
называется
предел отношения частного приращения
этой функции![]() по
по![]() к
приращению
к
приращению![]() ,
когда последнее стремится к нулю:
,
когда последнее стремится к нулю: .
.
Частной производной
по ![]() от
функции
от
функции![]() называется
предел отношения частного приращения
этой функции
называется
предел отношения частного приращения
этой функции![]() по
по![]() к
приращению
к
приращению![]() ,
когда последнее стремится к нулю:
,
когда последнее стремится к нулю: .
.
Пусть задана
функция ![]() .
Если аргументу
.
Если аргументу![]() сообщить
приращение
сообщить
приращение![]() ,
а аргументу
,
а аргументу![]() –
приращение
–
приращение![]() ,
то функция
,
то функция![]() получит
приращение
получит
приращение![]() ,
которое называется полным приращением
функции и определяется формулой:
,
которое называется полным приращением
функции и определяется формулой:![]() .
.